Все решения инженера @NICKПостроить проекции ромба. AC// п2- диагональ ромба ABCD. Вершина B принадлежит п1, вершина D равноудалена от плоскостей проекции
Построить проекции ромба. AC// п2- диагональ ромба ABCD. Вершина B принадлежит п1, вершина D равноудалена от плоскостей проекции п1 и п2. 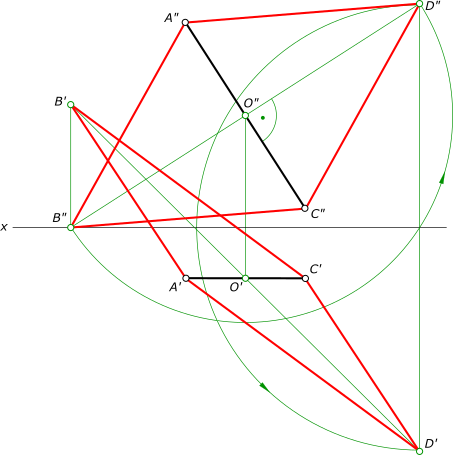
Построить проекции ромба. AC// п2- диагональ ромба ABCD. Вершина B принадлежит п1, вершина D равноудалена от плоскостей проекции п1 и п2 1. Диагонали ромба взаимно перпендикулярны и точкой их пересечения делятся пополам: - находим точку пересечения O(O', O") диагоналей ромба разделив пополам диагональ AC. - через точку O" проводим направление диагонали B"D" перпендикулярное A"C" до пересечения с осью x, где находим B" и затем D". 2. Из условия равного удаления точки D от п1 и п2: - находим D' 3. Из условия принадлежности точки B плоскости п1: - находим B' в пересечении направления диагонали O'D' и линии проекционной связи точки B. 4. Соединяем прямыми линиями найденные вершины B, D с вершинами AC и получаем искомые проекции ромба ABCD. Построить сферу со сквозным вырезом
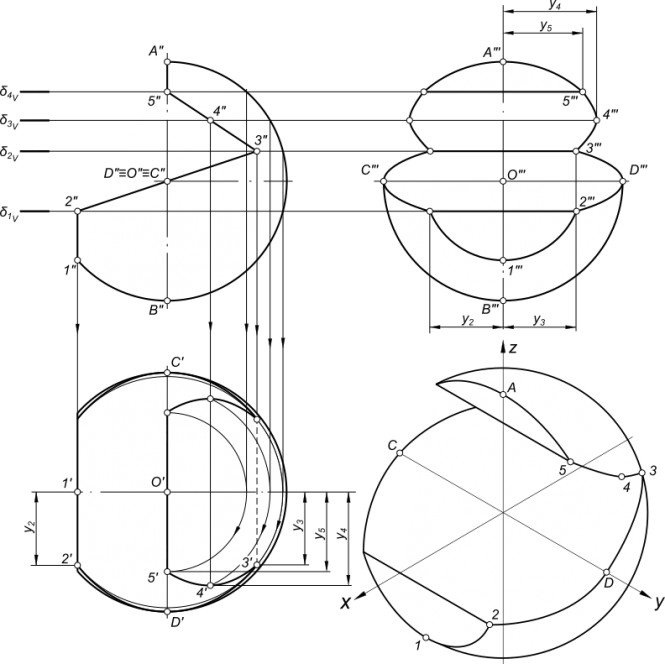
Построить сферу диаметром 80мм со сквозным поперечным вырезом призматической формы 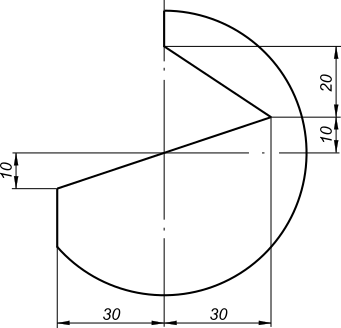
рисунок 1 Построить сферу диаметром 80мм со сквозным поперечным вырезом призматической формы Построить прямой круговой конус со сквозным вырезом призматической формы. Построения выполнить в трех проекциях
Построить прямой круговой конус со сквозным вырезом призматической формы. Построения выполнить в трех проекциях. М 1:1 
Построить прямой круговой конус со сквозным вырезом призматической формы. Построения выполнить в трех проекциях Комментарииспасибо большое)) выручили
Построить тени от прямых AB и CD общего положения
Построить тени от прямых AB и CD общего положения 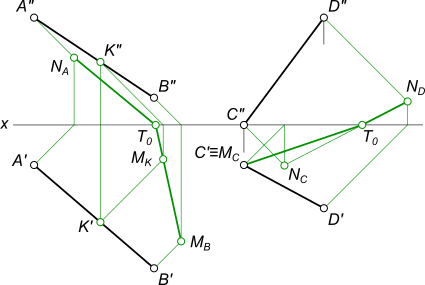
рисунок 1 Тень отрезка прямой AB располагается на обеих плоскостях проекций, она пересекает ось проекций в точке T0, называемой точкой перелома: Построение тени отрезка, располагающейся на плоскости проекций H: - находим тень точки B на горизонтальную плоскость проекции - MB; Построение тени отрезка, располагающейся на плоскости проекций V: - находим тень точки A на фронтальную плоскость проекции - NA; - произвольно берем точку C на отрезке AB; - находим тень точки K на одной из плоскостей проекции ; - соединяем прямой линией одноименные тени одного из концов и точки K продолжая ее до пересечения с осью проекций в точке T0; - соединяя прямой линией тень другого конца отрезка с точкой перелома T0 получаем тень отрезка на другой плоскости проекций. Тень отрезка прямой CD располагается на обеих плоскостях проекций, она пересекает ось проекций в точке T0, называемой точкой перелома: Построение тени отрезка, располагающейся на плоскости проекций V: - находим тень точки D на фронтальную плоскость проекции - ND; - находим мнимую тень точки C на фронтальную плоскость проекции - NC; - соединяя прямой линией тени концов отрезка NC и ND находим точку перелома T0 Построение тени отрезка, располагающейся на плоскости проекций H: - соединяем прямой линией тень точки MC и точку перелома T0. КомментарииПостроить пересечение поверхностей цилиндра и конуса
Построение пересечения поверхностей цилиндра и конуса выполняем способом вспомогательных секущих плоскостей, которые пересекут заданные поверхности по прямым линиям. Боковая поверхность цилиндра β занимает проецирующее положение к фронтальной плоскости проекций. Вспомогательные плоскости γ1, γ2, ..., γ5, проводим через образующие цилиндра и вершину конуса S, задавая их следы γ1V, γ2V, ..., γ5V строим γ1H, γ2H, ..., γ5H. В данном случае, коническая поверхность пересекается секущей плоскостью по прямым образующим конуса. Находим в пересечении горизонтальных следов вспомогательных плоскостей γ1H, γ2H, ..., γ5H с направляющей окружностью конуса α точки через, которые проходят соответствующие образующие конуса. В пересечении образующих конуса и образующих цилиндра, принадлежащих одной вспомогательной секущей плоскости, находим точки искомой линии сечения, которые соединяем плавной кривой линией. При построении проекций линии пересечения поверхностей на эпюре, в первую очередь, необходимо определить опорные точки, которые получаются при сечении поверхностей α и β плоскостями, касательными к одной, в частном случае - двум, из этих поверхностей. Выполняем определение видимости. КомментарииПостроить падающие тени от плоскости квадрата и его диагоналей
Построить падающие тени от плоскости квадрата ABCD и его диагоналей AC и BD 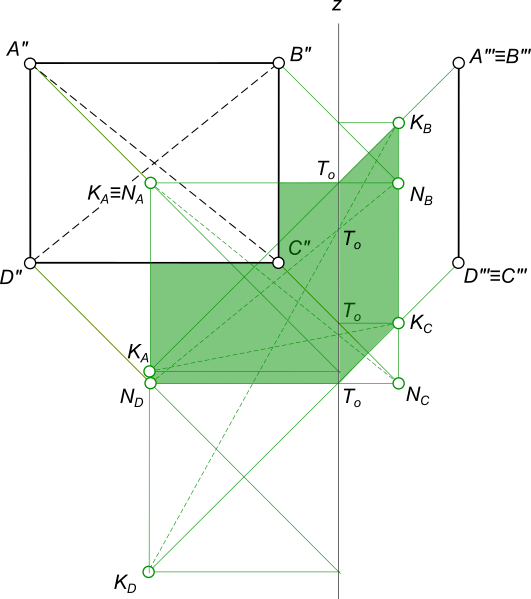
рисунок 1 Чтобы построить падающую тень плоской фигуры - четырехугольника ABCD на плоскостях проекций находим тени от каждой его вершины. Одноименные тени точек соединяем между собой прямыми линиями. To - точки преломления теней сторон и диагоналей квадрата. Стороны AD и BC параллельны профильной плоскости проекций и их падающие тени на нее параллельны оси z. Стороны AB и DC перпендикулярны профильной плоскости проекций и их падающие тени на фронтальную плоскость проекций перпендикулярны оси z. Падающие тени сторон AD и BC на профильную плоскость проекций параллельны оси z. Падающие тени сторон AB и DC на профильную плоскость проекций параллельны лучам света. Падающие тени диагоналей AC и BD на фронтальную плоскость проекций имеют искаженный вид. КомментарииПостроить падающие тени от плоскости квадрата и его диагоналей
Построить падающие тени от плоскости квадрата ABCD и его диагоналей AC и BD 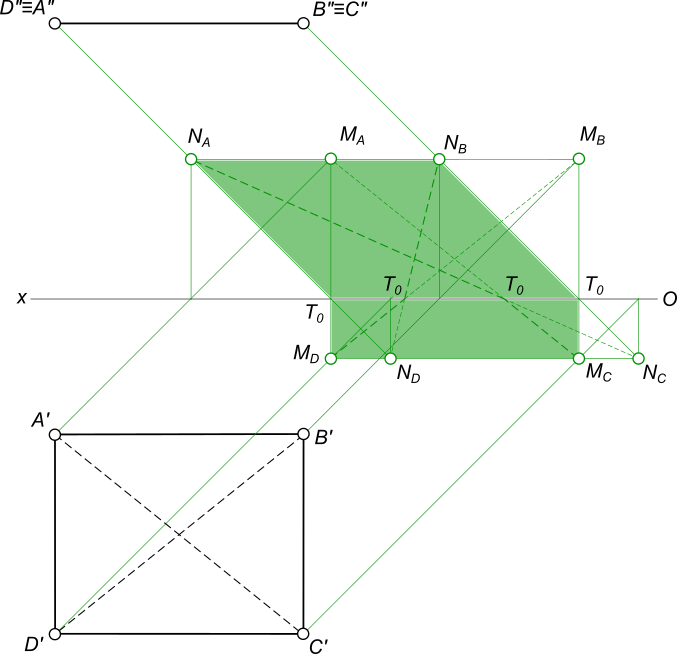
рисунок 1 Чтобы построить падающую тень плоской фигуры - четырехугольника ABCD на плоскостях проекций находим тени от каждой его вершины. Одноименные тени точек соединяем между собой прямыми линиями. To - точки преломления теней сторон и диагоналей квадрата. Падающая тень плоской фигуры - четырехугольника ABCD на горизонтальную плоскость проекций не имеет искажений Стороны AD и BC и их падающие тени на горизонтальную плоскость проекций перпендикулярны фронтальной плоскости проекций Стороны AB и DC и их падающие тени на горизонтальную плоскость проекций параллельны фронтальной плоскости проекций. Падающие тени сторон AD и BC на фронтальную плоскость проекций параллельны лучам света. Падающие тени сторон AB и DC на фронтальную плоскость проекций параллельны горизонтальной плоскости проекций. Падающие тени диагоналей AC и BD на фронтальную плоскость проекций имеют искаженный вид.. КомментарииПостроить правильную треугольную пирамиду
Правильная треугольная пирамида имеет в основании равносторонний треугольник и одинаковые боковые грани. Плоскость основания 1-2-3-4 образована двумя парами параллельных прямых 1-3, 2-4 и 1-2, 3-4, причем стороны 1-3 и 2-4 представляют собой горизонтали так как их фронтальные проекции параллельны оси x. Центр основания в точке A, аналогично определяем расположенным на горизонтали. Плоскость основания 1-2-3-4 занимает общее положение. 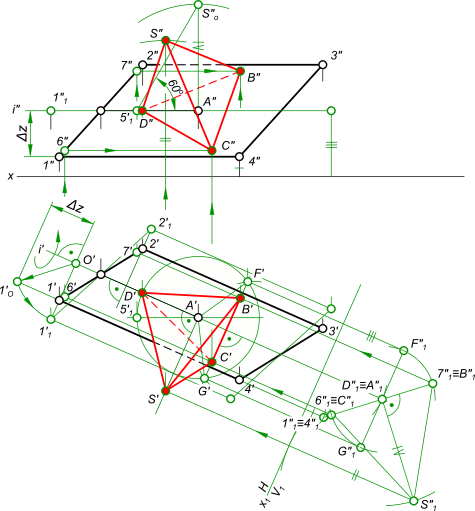
рисунок 1 Составим план решения 1. Построение в плоскости основания 1-2-3-4 равностороннего треугольника - основания пирамиды. 2. Определение высоты пирамиды построением заданного угла 60 между боковыми ребрами и основанием. 3. Построение проекций вершин пирамиды и определение видимости. План решения выполняем пошагово: 1. Переводим плоскость основания 1-2-3-4 в частное горизонтальное положение вращением вокруг горизонтали i, проходящей через точку A, находя при этом ее новое положение 11-21-31-41; 2. В плоскости основания 11-21-31-41 проводим окружность максимально возможного радиуса и через ее центр A проводим фронталь 51-A; 3. На фронтальной плоскости проекций строим боковое ребро задавая угол 60 наклона его к основанию; 4. Задав положение одной из вершин основания в точке D на оси вращения i, Находим остальные вершины основания пирамиды F и G, расположенными на равном расстоянии друг от друга на дуге окружности; 5. Построение проекций вершин основания пирамиды B и C и вершины S выполняем способом перемены плоскости проекций: а) плоскость основания пирамиды горизонтальна - D1, F1 и G1; б) плоскость основания пирамиды первоначального положения проходит через точки 1"1=4"1, D"1=A"1; в) на направлении перпендикуляра из точки A"1 откладываем высоту пирамиды и находим S"1; г) в пересечении линий проекционной связи точек S"1, перпендикуляра n' к плоскости основания находим S'1; д) в пересечении линий проекционной связи точек B"1 и C"1 c F'- G'находим точки B' и C'; е) в пересечении линий проекционной связи точек B' и C' c горизонталями проходящими через 6 и 7 находим точки B" и C"; ж) отложив от оси x по линии проекционной связи точки S отрезок II находим точки S". з) определение видимости КомментарииПостроить плоскость, касательную к цилиндру и параллельную прямой
Поверхность цилиндру α формируется движением образующей по направляющей - окружности в горизонтальной плоскости проекций. 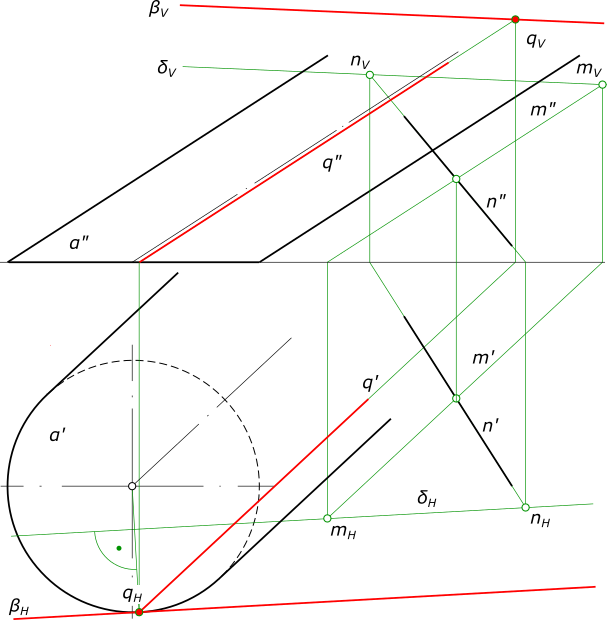
рисунок 1 1. Через прямую n проведем плоскость δ, параллельную образующим цилиндра α: a) Через произвольную точку прямой n проведем прямую m, параллельную образующим цилиндра α; b) находим следы прямых m и n с) Через следы прямых m и n проводим следы плоскости δ. 2. Восстанавливаем перпендикуляр к горизонтальному следу плоскости δ из центра окружности основания цилиндра и в пересечении его с окружностью находим горизонтальный след qH образующей цилиндра, через которую проходит искомая плоскость β. 3. Через следы образующей цилиндра qH и qV проводим следы плоскости β (βH, βV). Комментариипостроить эпюр точки B симметричной A относительно прямой m
построение эпюра точки B симметричной A относительно прямой m Здесь показан один из многих путей решения данной задачи. 1. Используем косоугольное проецирование с направлением S параллельным заданной прямой m: a) Через точку A проводим прямую n и находим следы nH, mH и nV, mV; b) находим следы плоскости α по следам параллельных прямых ее образующих nH, mH и nV, mV; c) находим следы kH и kV прямой k симметричной относительно прямой m на одноименных следах плоскости α. 2. Через точку A проводим плоскость β перпендикулярную параллельным прямым m, n и k плоскости α: a) Через точку A проводим горизонталь и фронталь плоскости β; b) Находим следы горизонтали и фронтали плоскости β; c) Проводим следы плоскости β через следы ее горизонтали h и фронтали f. 3. Находим точку B встречи прямой k с плоскостью β: a) Находим линию пересечения 1 - 2 плоскостей α и β; b) Находим искомую точку B в пересечении линии 1-2 с прямой k. 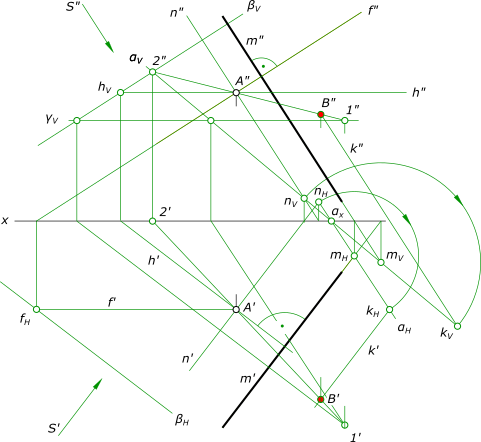
рисунок 2 КомментарииПостроить линию пересечения поверхностей призмы и сферы
Решения задачи на пересечение поверхностей, подразумевает построение их линии пересечения. Для того чтобы построить линию пересечения необходимо найти достаточное количество ее точек, применяя вспомогательные поверхности (посредники). 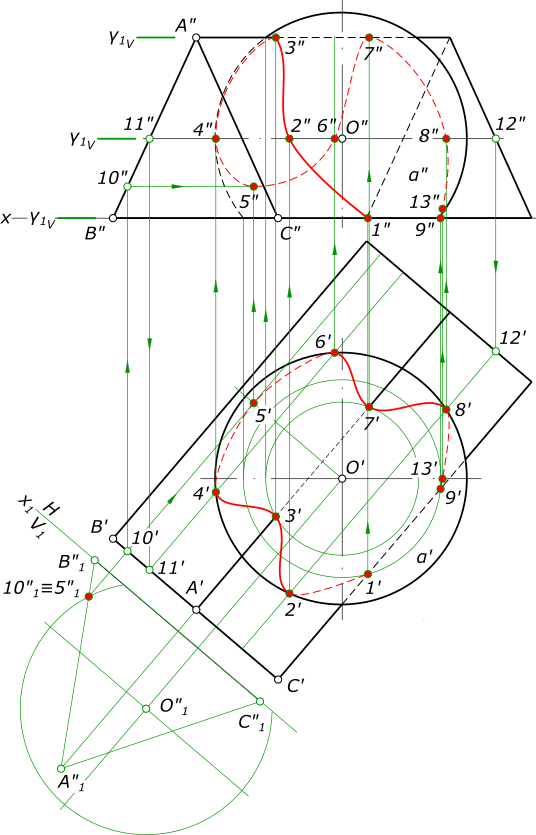
рисунок 1 Здесь вспомогательные поверхности (посредники) - плоскости γ1, γ2 и γ3, пересекающие заданные поверхности призмы и сферы по прямым линиям и окружностям соответственно. Переменой плоскости проекций находим самую низкую точку линии пересечения на грани AB призмы. Найденные точки 1, 2, ..., 9 линии пересечения соединяем плавной кривой линией Выполняем определение видимости на плоскостях проекций. КомментарииПостроить точки пересечения прямой с поверхностью вращения
Пересечение прямой с поверхностью вращения - это задача по определению точек встречи прямой с поверхностью вращения Поверхность α представляет собой поверхность вращения с образующей в виде кривой линии, а прямая d занимают общее положение. Решать задачу на пересечение прямой с поверхностью вращения следует, применяя алгоритм пересечения прямой с поверхностью: - Заключаем прямую d в вспомогательную горизонтально проецирующую плоскость γ, которая пересечет поверхность вращения по кривой линии, которую необходимо построить; - Находим точки пересечения 1 и 2 этой плоскости с основанием поверхности вращения; - Находим наивысшую точку N линии сечения поверхности вращения; - Вспомогательная плоскость уровня δV дает возможность построить точки 3 и 4 линии сечения; - Соединяем плавной кривой точки 1, 2, 3, 4 и N и получаем линию сечения - Находим точки E и K пересечения прямой с линией сечения поверхности вращения. 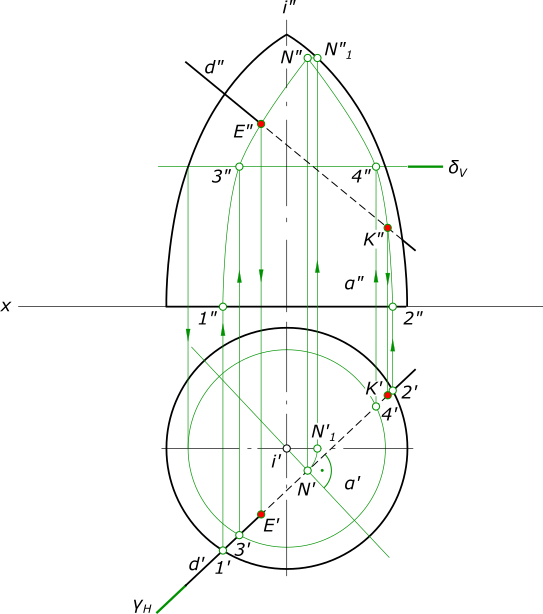
рисунок 1 Пересечение прямой с поверхностью вращения - это также задача по определению видимости с помощью конкурирующих точек Для горизонтальной плоскости проекций. Кривые 1, 3, N и 2, 4, N видимы. Прямая d видима за пределами отрезка EK. Для фронтальной плоскости проекций. Кривая 1, 3, N видима, а кривая 2, 4, N невидима. Прямая d видима до точки E и за пределами очерка поверхности вращения. КомментарииПровести плоскость через точку
Точка принадлежит плоскости, если через нее проходит прямая принадлежащая данной плоскости 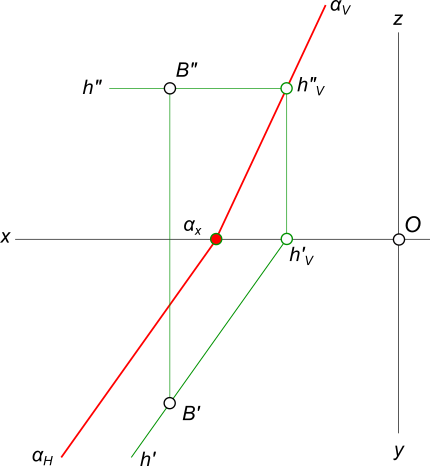
рисунок 1 Через точку проводим произвольную прямую h и находим ее следы Проводим следы плоскости α через следы прямой h Комментариипомоги пожалуйста.
В чем Вам помочь?
Nick, требуется твоя помощь по построению планов скоростей и ускорений. Срочно
Можете помочь с решением интересной задачи?или проверить мое решение?
А не могли бы Вы к моей задачи сделать чертеж, если не сложно (просто уже какой день сижу, все не получается((
Могу ли я С вами связаться в другом месте?в Вотсапе, вайбере или контакте?чтобы задать пару вопросов?думаю так будет быстрее)
Просто недавно на этом сайте и еще не очень разобрался что куда писать)поэтому было бы не плохо связаться в другом месте на пару вопросов)если у Вас не получится ,скажите об этом тоже)
Мне вот сегодня подсказали, что нужно решать начиная с замены)мы прямую "а" переводим а в положение уровня (2раза). Затем рисуем конус конуса вращения,где Rосн=AC,а длинна образующей =ВС. Потом одна или несколько(скорее всего 2) будут параллельны прямой "в". Мы берем плоскость параллельную плоскплоскости (А,в) и расскажем ей конус через вершину В. Вот как-то так)
Есть ли у Вас какие-нибудь мысли?)
Надо общаться на странице вашей задачи. Зачем вы перешли на эту задачу?
Сейчас себе на страницу скину объяснение преподавателя)может поможет вам)
То Есть мы находим множество точек ВС построением конуса вращения по длинам гепатинузы и карета, а затем отбираем нужное нам, пересечением конуса с прямой ВС используя условие параллельности Где ВС параллельна плоскости (А,в)
Здравствуй,ты не мог бы мне помочь с начертательной геометрией?))
Здравствуйте, почему Вы ко мне обращаетесь на «ты»? Вас, что не научили правилам «вежливого обращения». И почему Вы пишете мне здесь в чужой задаче, а не в своих?
Можно ли договориться с вами про решение срочных заданий на определённое время за оплату?
Это надо смотреть по каждому заданию. Разместите их на страницах сайта.
Помоги пожалуйстаааа с проекциями и тех рисунком пирамиды!!!!у меня в профиле задача!!могу за оплату!!!
Извините за невежливое обращение к вам , помогите пожалуйста мне!
Здравствуйте, не могли бы вы мне помочь?
Добрый вечер,. Можете мне помочь?
Через точку А провести фронтально-проецирующую плоскость, параллельную отрезку МК А(25;25;20) М(55;30;25) К (25;15;10)
Пожалуйста записывайте вторую задачу не через комментарий, а как положено.
Так Вы сможете помочь мне?
Спасибо. Можно ли с Вами связаться напрямую? Я впервые на этом сайте, сложно ориентироваться
Можете без моего способа решения задач решить эти две задачи...оплата...
Здравствуйте,не могли бы мне помочь. На этом сайте недавно. Не понимаю еще как пользоваться посмотрите задачу ...
Да, пожалуйста. Для этого Вам надо записать свою задачу. Посмотрите как это делается в задаче, например, https://ingr.fxyz.ru/tasks/1627/ . Записав задачу Вы получите свою страницу на сайте, там Вам будет удобнее задать интересующие Вас вопросы.
@nick, Оплатил задание.
Nick, когда скинете решение задачи?
@nick помоги пожалуйста с заданием по теории машин и механизмов, позже скину задание
Nick помоги пожалуйста
Nick, помоги с заданием)
@nick,произвёл оплату за задание
Вы сможете решить задачи, если да, то сколько это стоит и как мне оплатить?
Комментарий id320502251 свяжитесь, пожалуйста со мной в вк. Антонова Валерия
@nick, привет, помоги пожалуйста мне с заданием. Нужно написать процесс сборки шестеренчатого насоса по твоему чертежу
Нужна ваша помощь
Доброе утро! Мне очень срочно нужно решить задачи!! В течении часа, вы сможете мне помочь и сколько это будет стоить?
О каких задачах идет речь? Запишите свои задачи, тогда будет видно.
здравствуйте. помогите пожалуйста, очень срочно
Здравствуйте, чтобы получить помощь необходимо записать свою задачу. А здесь у вас какие-то проблемы. Вероятно это вот что: при прохождении регистрации на ваш е-майл приходит письмо где вы проходите по ссылке. Перед вами открывается окно редактирования вашего аккаунта. После его окончания необходимо завершить регистрацию закрытием сайта. Затем вы открываете сайт вновь выбираете Войти и записываете свою задачу.
@nick добрый день! Как можно получить Ваше решение в формате dwg на ВЕНТИЛЬ УГЛОВОЙ
Привет, очень нужна помощь в построении проекции линии пересечения:( единственная задача в моем профиле
@nick Привет, можете помочь? Тема: разрезы. https://ingr.fxyz.ru/tasks/2802
@nick привет можешь помочь ? тема https://ingr.fxyz.ru/branches/101/
здравствуйте, можете пожалуйста помочь?
Найти точки пересечения поверхности цилиндра прямой линией
Пересечение прямой с поверхностью цилиндра - это задача по определению точек встречи прямой с поверхностью цилиндра. Поверхность цилиндра представляет собой поверхность вращения с образующей в виде прямой линии. 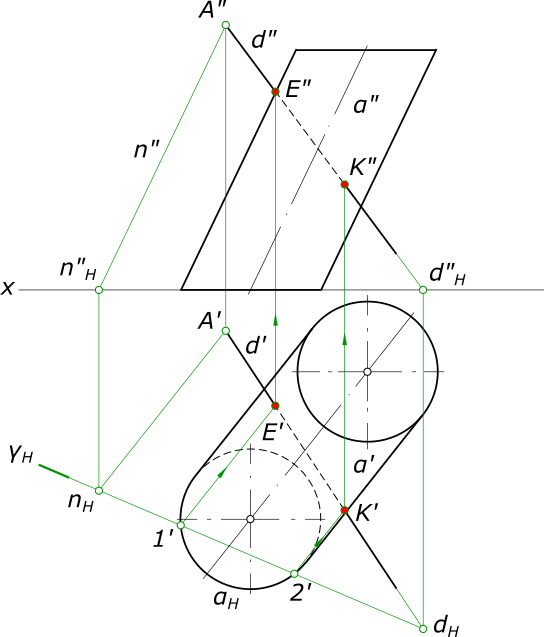
рисунок 1 Здесь прямая d занимают общее положение и поверхность цилиндра α формируется прямыми пересекающимися в несобственной точке S. Решать задачу на пересечение прямой с цилиндром следует, применяя алгоритм пересечения прямой с поверхностью: - Заключаем прямую d в вспомогательную плоскость γ, которая пересечет цилиндр по прямым линиям - образующим. Плоскость γ задаем пересечением в точке A прямой d и прямой n параллельной образующим цилиндра; - Находим точки пересечения 1 и 2 этой плоскости с основанием цилиндра, для чего строим горизонтальный след плоскости - γH по следам прямых nH и dH. - В пересечении образующих цилиндра 1 и 2 с прямой d находим искомые точки E и K пересечения прямой с поверхностью цилиндра. Пересечение прямой с поверхностью цилиндра - это также задача по определению видимости с помощью конкурирующих точек: - для горизонтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK; - для фронтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK. КомментарииПостроить проекции прямой
1) В пересечении линий проекционной связи точек bV и bW с координатными осями находим их проекции b'V, b'"V и b"W, b'W. 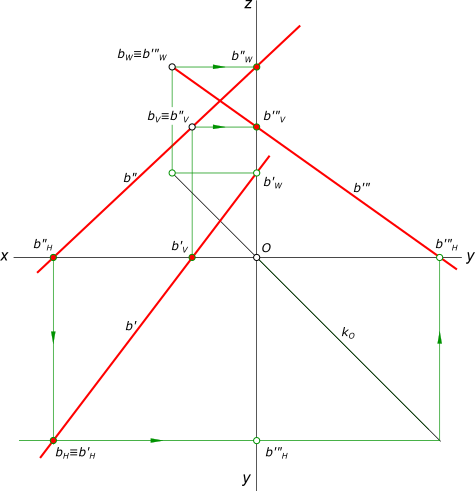
рисунок 1 2) Соединяем прямыми линиями следующие пары точек: bW и b'"V, bV и b"W, b'W b'V и отмечаем их при этом как b'", b", b'. 3) В пересечении линии проекционной связи, проведенной из точки b"H и b' находим bH . КомментарииНайти линию пересечения треугольной призмы плоскостью
Боковые ребра призмы представляют собой горизонтально проецирующие прямые. Поэтому проекции вершин сечения совпадают с проекциями этих ребер на плоскостьH 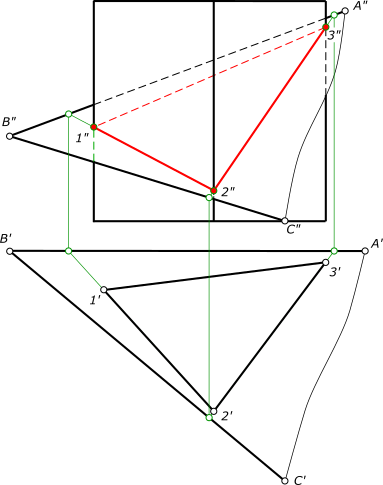
рисунок 1 Фронтальные проекции вершин сечения определяются, исходя из условия их принадлежности секущей плоскости и боковым ребрам призмы. КомментарииНайти точку пересечения прямой с плоскостью треугольника
1) Задаем направление вспомогательного проецирования S параллельным стороне BC треугольника. На плоскость H треугольник проецируется в прямую AC≡B, а отрезок 1—2 в отрезок 1—2. 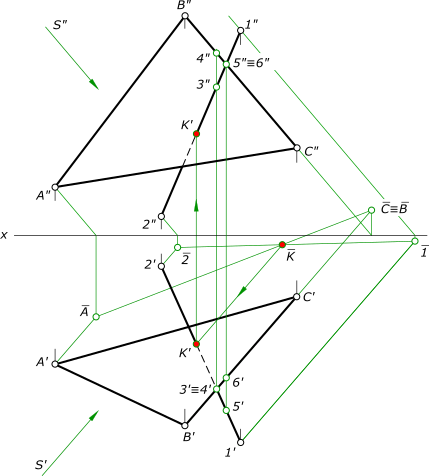
рисунок 1 2) Точку пересечения K этих прямых проецируем в обратном направлении на исходные проекции прямой. 3) Определяем видимость прямой: a) на горизонтальной плоскости проекций: отмечаем конкурирующие точки 3 и 4, принадлежащие стороне BC треугольника и прямой 1—2 соответственно. Точка 4 удалена от плоскости H, более чем точка 3 значит прямая до точки пересечения K с плоскостью треугольника будет невидима; b) на фронтальной плоскости проекций: отмечаем конкурирующие точки 5 и 6, принадлежащие прямой 1—2 и стороне BC треугольника соответственно. Точка 5 удалена от плоскости V, более чем точка 6 значит прямая до точки пересечения K с плоскостью треугольника будет видима. КомментарииНайти точку пересечения прямой с плоскостью
1) Проводим через прямую горизонтально-проецирующую плоскостьγ и отмечаем точки ее пересечения со сторонами треугольника. Точка пересечения стороны 2—3 на фронтальной плоскости проекций не определяется ввиду ее профильного положения. Заменив в плоскости треугольника сторону 2—3 на прямую общего положения 2—5, определяем вторую точку 6 линии пересечения плоскостей 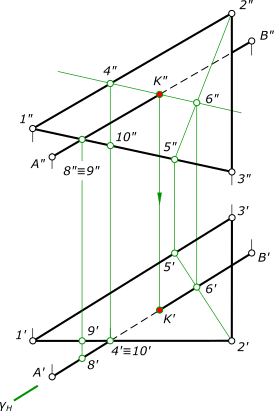
рисунок 1 2) Определяем в пересечении прямой AB и линии пересечения плоскостей 4—6 искомую точку K встречи прямой с плоскостью треугольника. 3) Определяем видимость прямой: a) на горизонтальной плоскости проекций: отмечаем конкурирующие точки 4 и 10, принадлежащие стороне 1—2 треугольника и прямой AB соответственно. Точка 4 удалена от плоскости H, более чем точка 10 значит прямая до точки пересечения K с плоскостью треугольника будет невидима; b) на фронтальной плоскости проекций: отмечаем конкурирующие точки 8 и 9, принадлежащие прямой AB и стороне 1—3 треугольника соответственно. Точка 8 удалена от плоскости V, более чем точка 9 значит прямая до точки пересечения K с плоскостью треугольника будет видима. КомментарииЗдравствуйте. А можно, пожалуйста, Вас попросить решить задачу наподобие такой же?
Найти горизонтальную проекцию горизонтали BC плоскости α
1) Проводим через точку A горизонталь h в плоскости α и находим ее фронтальный след hV. 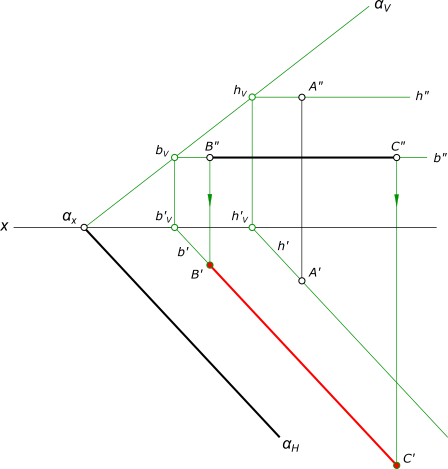
рисунок 1 2) Проводим через точку hV фронтальный след αH плоскости α 3) Проводим через точки отрезка B"C" горизонталь b" в плоскости α и отмечаем ее фронтальный след bV. Из горизонтальной проекции b'V проводим b' параллельно αH 4) Соединяем 1' и 2' прямой линией 5) Находим горизонтальную проекцию отрезка B'C' в пересечении линий проекционной связи точек B и C с b'. КомментарииПостроить горизонтальную проекцию прямой
1) Продлеваем фронтальную проекцию E"F" прямой до пересечения с A"B", отмечаем здесь точку 1". 2) Находим горизонтальную проекцию 1' в пересечении линии связи точки 1 с A'B' 3) Находим горизонтальную проекцию 2' в пересечении линии связи точки 2 с B'C' 4) Соединяем 1' и 2' прямой линией 5) Находим горизонтальную проекцию E'F' в пересечении линий связи точек E и F с 1'—2'. 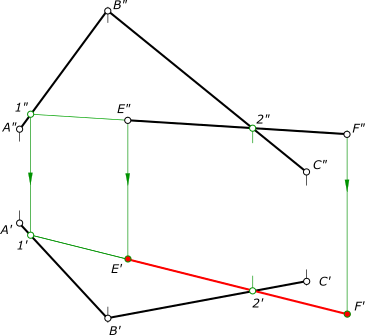
рисунок 2 КомментарииКакую ошибку допустил учащийся?
взаимно перпендикулярные прямые могут быть при этом не только пересекающимися, но и скрещивающимися. КомментарииЧерез точку A(-3;4;-3) провести прямую параллельную плоскостям 3x+4y-2z+7=0 и x-2z+5=0
1. Построить проекции точки A 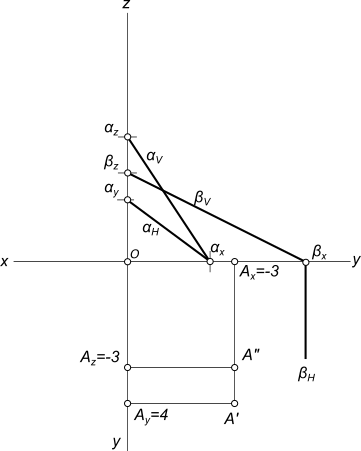
рисунок 1 2. Строим следы плоскости α (3x+4y-2z+7=0) a) z=0; 3x+4y+7=0 αH; y=0; 3x+7=0, x=-7/3, x=-2,33 x=0; 4y+7=0, y=-7/4, y=-1,75 b) y=0; 3x-2z+7=0 αV; x=0; -2z+7=0, z=3,5 z=0; 3x+7=0, x=-2,33 3) Строим следы плоскости β (x-2z+5=0) βV x=0; -2z+5=0, z=5/2, z=2,5 z=0; x+5=0, x=-5 Строим линию пересечения 1—2 заданных плоскостей α и β 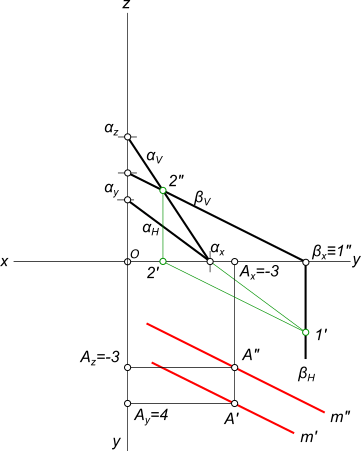
рисунок 3 Строим линию m параллельную плоскостям α и β m'//1'—2' и m"//1"—2" Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |



Комментарии