Все решения инженера @NICKКак называется прямая АВ, имеющая следующие координаты: А(10,30,50); В(10,15,40)
Как называется прямая АВ, имеющая следующие координаты: А(10,30,50), В(10,15,40); A(50,-10,-70), B(-10,-10,-5); A(20,30,40), B(20,30,-40). Прямая m называется: горизонталью, если координата z = const для всех точек прямой. На эпюре m2 II x ; фронталью, если координата y = const для всех точек прямой. На эпюре m1 II x ; профильной прямой, если координата x = const для всех точек прямой. На эпюре m1 II z, m2 II z ; Для прямой AB координата ... = const, Следовательно прямая AB — ... Прямая m называется горизонтально-проецирующей если: Для прямой AB координаты x = const, y = const. Следовательно прямая AB — ... Прямая m называется фронтально-проецирующей если: Для прямой AB координаты x = const, z = const. Следовательно прямая AB — ... Прямая m называется профильно-проецирующей если: Для прямой AB координаты z = const, y = const. Следовательно прямая AB — ... Построить т.(10, -10, -15). Определить ее положение в пространстве?
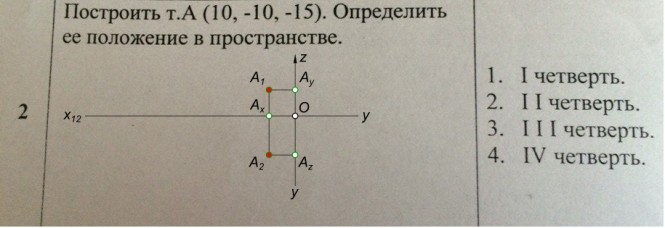
Построить точку A(10, -10, -15). Определить ее положение в пространстве. Пространство разделено на четверти I, II, III и IV Знаки координат x, y, z в четвертях пространства: +, +, + - четверть I +, –, + - четверть II +, –, – - четверть III +, +, – - четверть IV Таким образом, точка расположена в ... четверти пространства. КомментарииКакая из точек ближе расположена к плоскости проекций П2?
Точки A, B, C и D заданы проекциями A1 и A2, B1 и B2, C1 и С2 и D1 и D2 соответственно. Проекция точки с индексом 1 определяется координатами x и y. Проекция точки с индексом 2 определяется координатами x и z. Удаленность точки от плоскости проекций П2 определяется ее координатой IyI. |Ay| < |By| < |Dy| < |Cy| Таким образом из точек A, B, C и D ближе расположена к плоскости проекций П2 точка ... A. КомментарииПожалуйста покажите рисунки.
В каком случае заданная плоскость не параллельна плоскости Р(АВС)
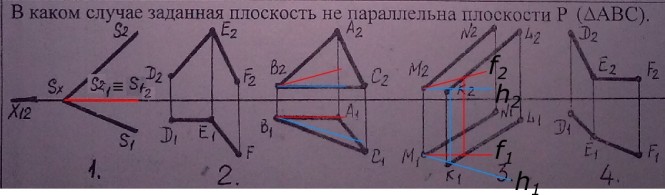
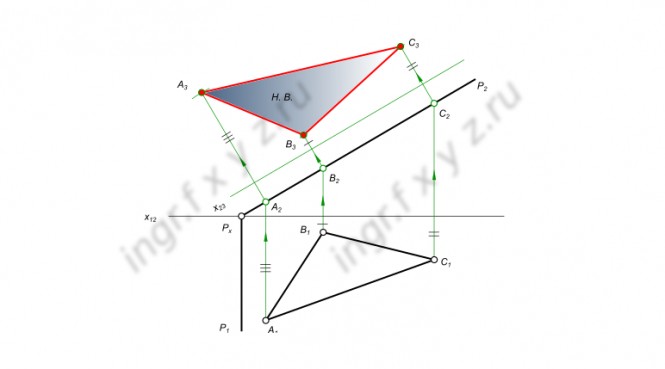
В каком случае заданная плоскость не параллельна плоскости Р(АВС) Плоскости параллельны когда одна из них содержит пересекающиеся прямые параллельные пересекающимся прямым другой плоскости. На представленном эпюре Монжа, плоскость P(ΔABC) содержит пересекающихся в точке В прямые - горизонталь BC и фронталь AB. В случаях 2. и 4. плоскости, сравниваемые с плоскостью P, представлены пересекающимися в точке E прямыми. Здесь ответ на вопрос задачи можно дать без каких-либо дополнительных построений. В случае 1. плоскость, сравниваемая с плоскостью P, представлена пересекающимися в точке Px прямыми P1 и P2. Здесь ответ на вопрос задачи можно дать, выполнив построение недостающих проекций следов P1 и P2. В случае 3. плоскость, сравниваемая с плоскостью P, представлена параллельными прямыми. Для проведения сравнения плоскости должны быть выражены одинаково. Поэтому, плоскость, заданную параллельными прямыми, следует представить с помощью таких же пересекающихся прямых - горизонтали и фронтали. КомментарииНайти натуральную величину АВС методом перемены плоскостей проекций.
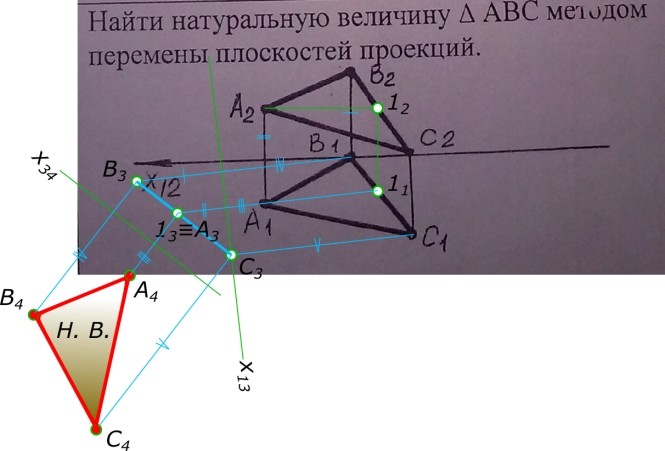
Найти натуральную величину АВС методом перемены плоскостей проекций. КомментарииПостроить точку встречи прямой АВ с плоскостью Р ( СD EF)
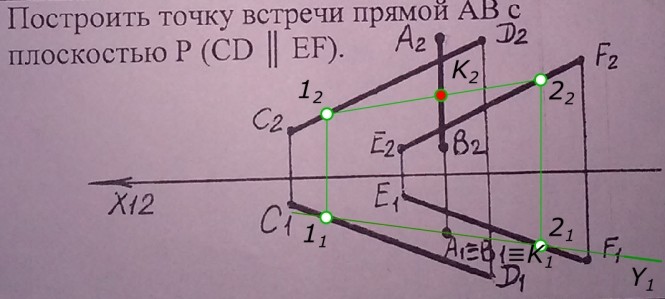
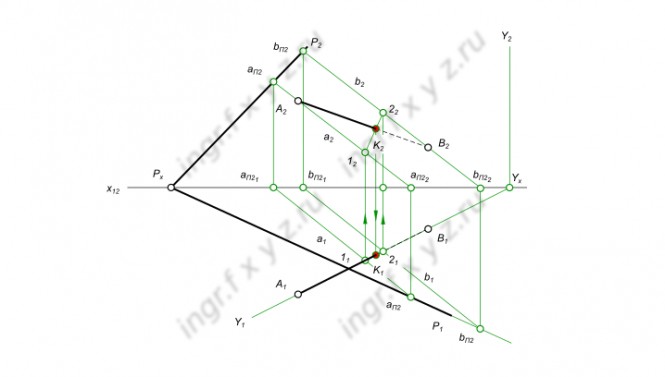
Построить точку встречи прямой АВ с плоскостью Р ( СD EF) Точку встречи прямой AB с плоскостью Р ( СD EF) находим с помощью вспомогательной секущей плоскости Υ, проведенной через заданную прямую. Определяем линию пересечения 1 - 2 вспомогательной плоскости Υ с заданной и в пересечении ее с прямой AB находим искомую точку встречи. КомментарииПостроить линию пересечения плоскостей P и Q
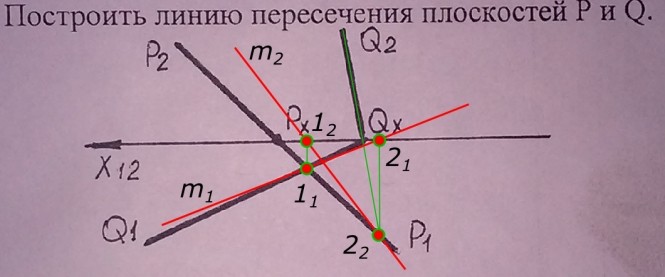
Построить линию пересечения плоскостей P и Q Линию пересечения m плоскостей P и Q находим определяя точки 1 и 2 пересечения одноименных следов данных плоскостей. КомментарииПостроить фронтальную проекцию точки А, принадлежащей плоскости Р.
Построить фронтальную проекцию точки А, принадлежащей плоскости Р. 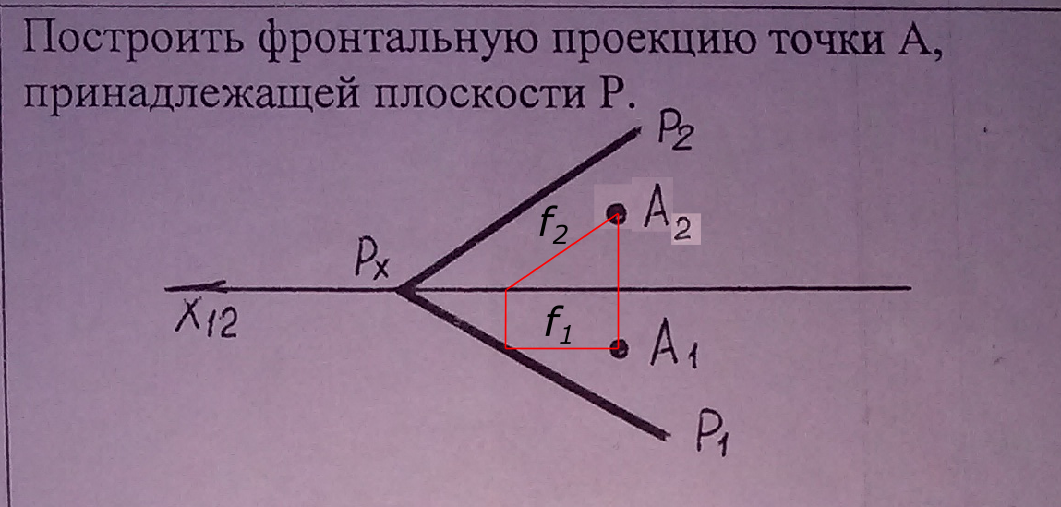
рисунок 1 Точка принадлежит плоскости, если она принадлежит прямой принадлежащей данной плоскости. На эпюре Монжа через горизонтальную проекцию A1 точки A проводим одноименную проекцию фронтали f1 - прямой принадлежащей плоскости P. На фронтальной плоскости проекций проводим f2 и в пересечении ее с линией проекционной связи точки А находим искомую проекцию А2. КомментарииКакая из плоскостей параллельна прямой АВ?
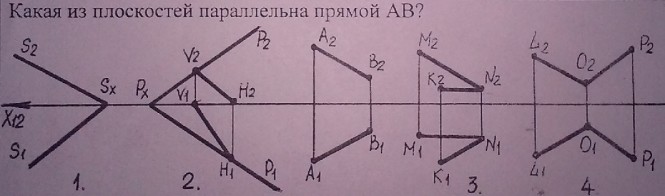
Какая из плоскостей параллельна прямой АВ? Плоскость параллельна прямой если в ней можно провести прямую параллельную заданной прямой. На эпюре Монжа одноименные проекции параллельных прямых параллельны. На представленном эпюре: A1B1 // L1O1 и A2B2 // L2O2. КомментарииКакая из точек лежит в плоскости Р?
Какая из точек лежит в плоскости Р? Плоскость P - горизонтально-проецирующая так как ей принадлежит прямая перпендикулярная П1, это фронтальный след P2 плоскости P. На эпюре Монжа все точки, принадлежащие горизонтально-проецирующей плоскости P, имеют горизонтальные проекции на ее горизонтальном следе P1: B1 ≡ P1. B ∈ P КомментарииЧерез точку А провести горизонтальную плоскость.Задать ее параллельными прямыми(m n)
Через точку А провести горизонтальную плоскость.Задать ее параллельными прямыми(m n) 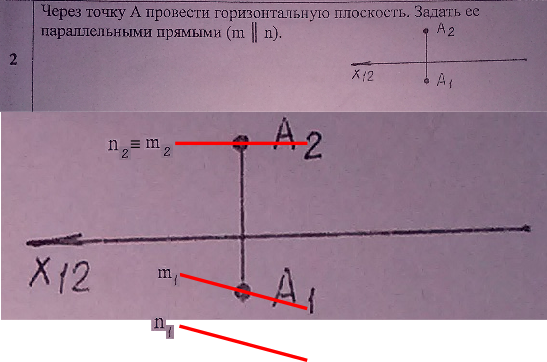
рисунок 1 Точка принадлежит плоскости если она принадлежит прямой принадлежащей плоскости. На эпюре Монжа проекции точки A(A1, A2) принадлежат одноименным проекциям прямой m(m1, m2) Признак параллельности прямых на эпюре Монжа - параллельность их одноименных проекций: m1//n1 и m2//n2. Прямые принадлежат горизонтальной плоскости, поэтому их фронтальные проекции совпадают и параллельны оси x. КомментарииКакая фронтально-проецирующая плоскость задана треугольником?
Какая фронтально-проецирующая плоскость задана треугольником? 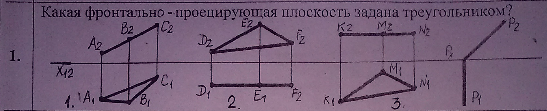
рисунок 1 Очевидно это начертательная геометрия в режиме тестирования. Ответ: 1. и 3. Признак фронтально проецирующей плоскости на эпюре Монжа - фронтальная проекция плоскости вырождается в прямую линию. КомментарииАксонометрическое изображние детали
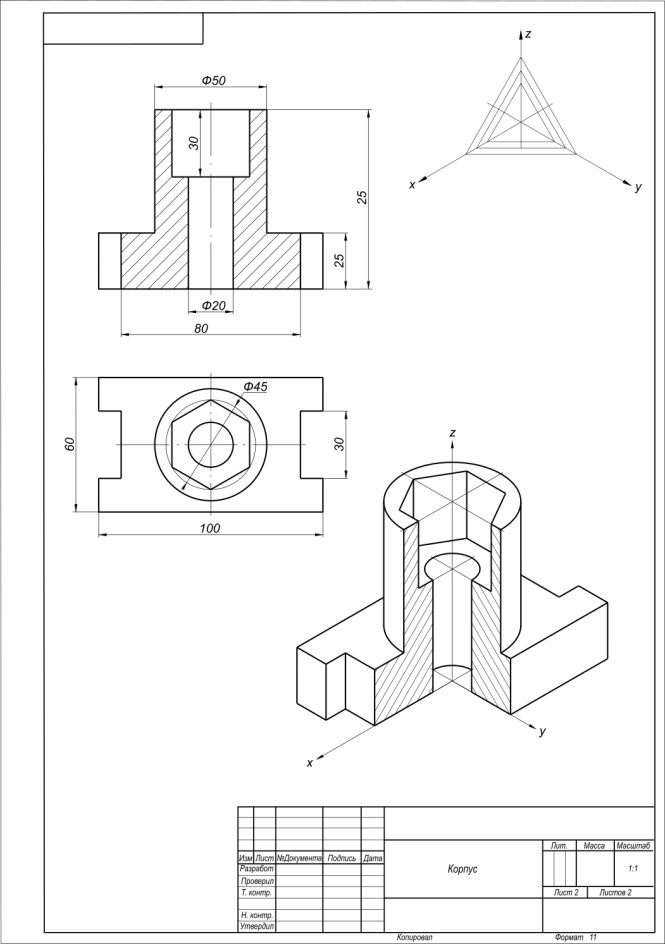
По предложенным изображениям выполнить чертеж детали с необходимыми разрезами, проставить размеры. Построить аксонометрическое изображение детали. КомментарииПостроить натуральную величину АВС, который принадлежит плокости Р методом перемены плоскостей проекций
Построить натуральную величину АВС, которая принадлежит плоскости Р, методом перемены плоскостей проекций. Построить прямоугольник
Построить прямоугольник ABCD с большим основанием BC на прямой m, исходя из условия, что отношение сторон равно 2. 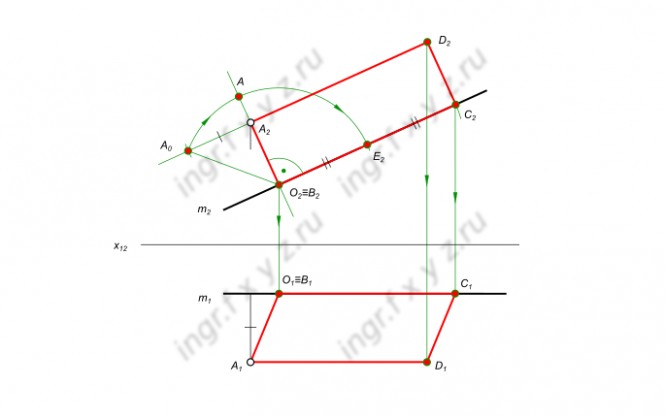
Построить прямоугольник ABCD с большим основанием BC на прямой m, исходя из условия, что отношение сторон равно 2 КомментарииВ сфере цилиндрическое сквозное отверстие, построить недостающие виды
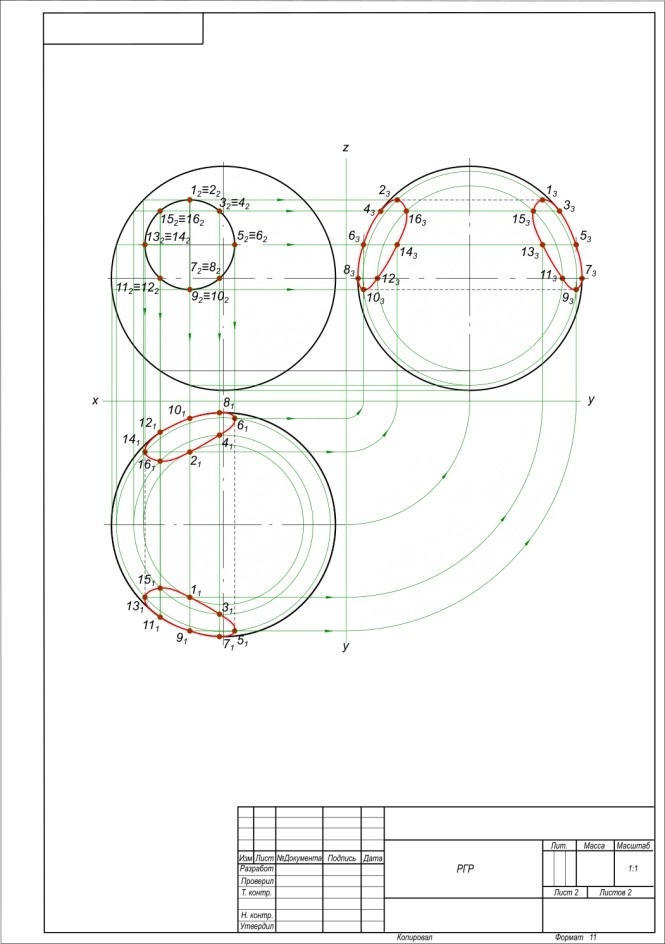
В сфере цилиндрическое сквозное отверстие, построить недостающие виды.. Построить в трех проекциях линию пересечения поверхностей сферы и цилиндра. КомментарииПосторить точку встречи прямой АВ с плоскостью Р
Построить точку встречи прямой АВ с плоскостью Р КомментарииПосторить точку встречи прямой АВ с плоскостью Р
Построить точку встречи прямой АВ с плоскостью Р КомментарииПосторить точку встречи прямой АВ с плоскостью Р
Построить точку встречи прямой АВ с плоскостью Р КомментарииЧерез т А провести перпендикуляр к плокости Р (АВС)
Через т А провести перпендикуляр к плоскости Р (АВС) 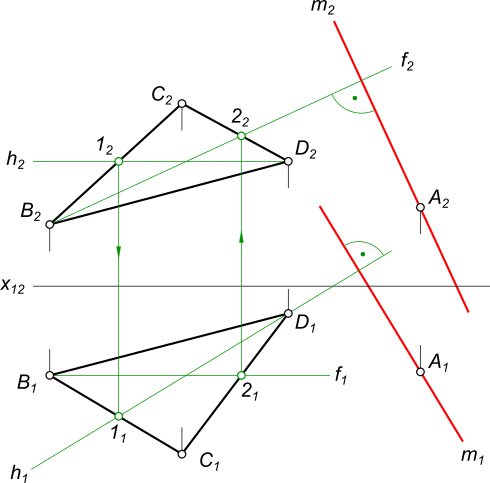
рисунок 1 Согласно признаку перпендикулярности прямой плоскости - прямая должна быть перпендикулярна главным линиям плоскости. Применительно к данному чертежу прямая m перпендикулярна горизонтали h и фронтали f плоскости P(ABC) Построить горизонтальную проекцию прямой АВ,принадлежащей плокости Р
Построить горизонтальную проекцию прямой А-В(..., А2-В2) общего положения, принадлежащей профильно-проецирующей плоскости Р(РП1, РП2) 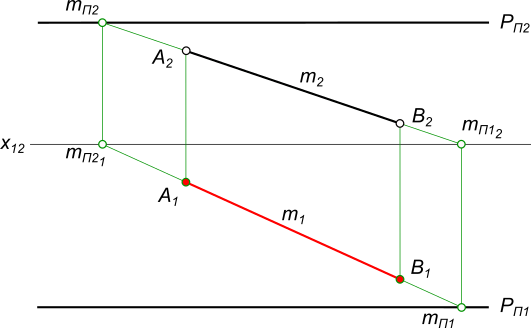
рисунок 1 Выражаем проекцию отрезка А2-В2 через m2 и находим след mП2 и mП12. Далее и находим след mП1 и mП21 через которые проводим m1. Проекции отрезка А1-В1 находим в пересечении m1 с линиями проекционной связи точек А и В. КомментарииСделать развертку наклонной усеченной призмы с вырезом
Сделать развертку наклонной усеченной призмы со сквозным отверстием В основании наклонной усеченной призмы правильный шестиугольник ABCDEF. Построена горизонтальная проекция линии пресечения поверхности призмы и цилиндра. Построено нормальное сечение призмы плоскостью β Развертка поверхности наклонной призмы выполнена способом нормального сечения. Построена натуральная величина сечения призмы плоскостью α КомментарииВыполнить резьбовые соединения деталей сборочного чертежа с их упрощенным изображением по ГОСТ 2.315-68
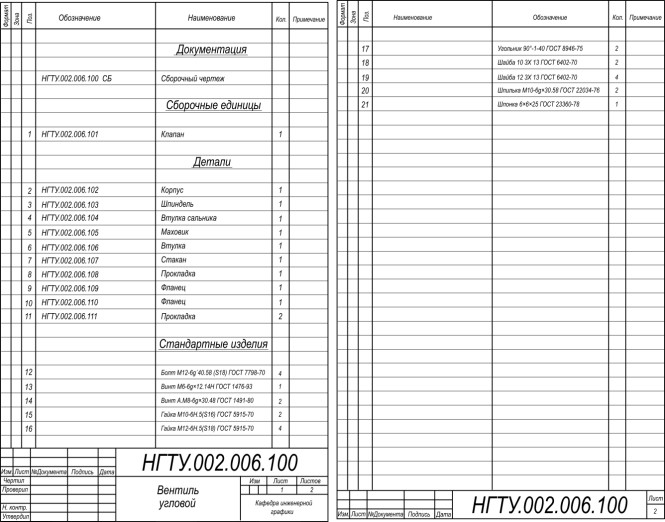
Заполнена в спецификации графа “Стандартные изделия”. КомментарииВыполнить резьбовые соединения деталей сборочного чертежа с их упрощенным изображением по ГОСТ 2.315-68
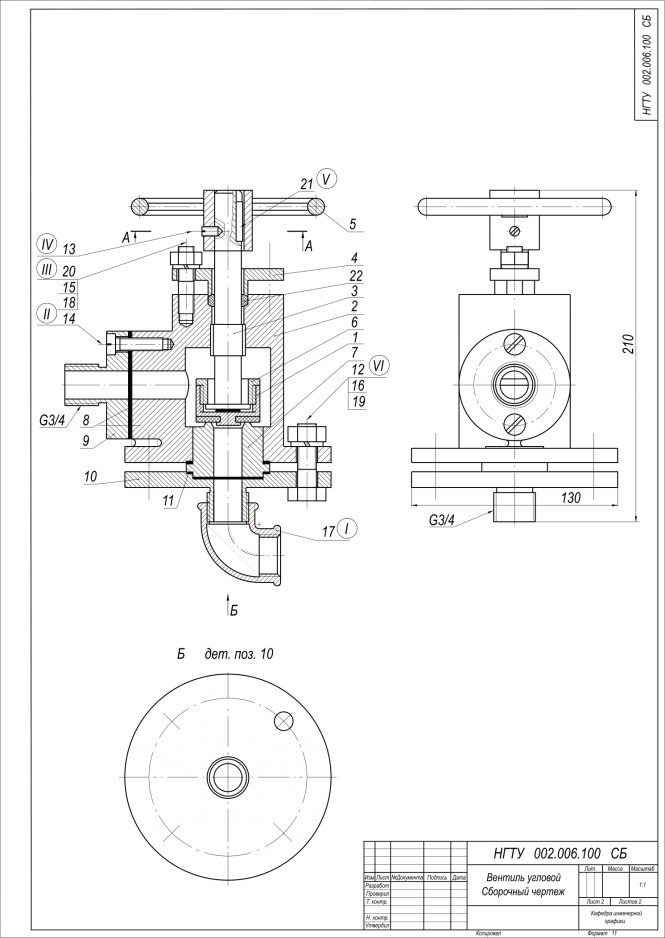
На чертеже выполнить соединения с метрической и трубной резьбой: I – соединен фланец 10 с корпусом 2 болтами 12 (резьба М12), установлены пружинные шайбы 19 и гайки 16. Конструкция и размеры болтов установлены ГОСТ 7798-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры болта: резьба M = 12; шаг 1,5 мм; диаметр стержня d1 = 12 мм; размер под ключ S = 18 мм; высота головки k = 7,5 мм; диаметр описанной окружности e = 19,9 мм; длину резьбы l0 = 30 мм. m = 10,8 мм; Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры болта:
Длина болта определяется по формуле:
$ l = b1+b2+S+m+(2 ÷ 3)P $ Где: b1 и b2 - толщина соединяемых деталей; S - толщина шайбы; m - высота гайки; P - шаг резьбы. Толщина соединяемых деталей, в данном случае, определяется по сборочному чертежу и составляет b1+b2 = 26 мм. Толщину шайбы S = 3 мм находим в ГОСТ 6402-70: Шайбы пружинные. Высота гайки m = 10,8 мм находим в ГОСТ 5915-70 Гайки шестгранные ... . Подставляем все найденные значения в формулу длины болта:
$ l=26+3+10,8+(2÷3)1,5=39,4 +3÷39,4 +4,5=40 мм $ Принимаем длину болта равной ближайшему значению из таблицы ГОСТа; II – выполнено соединение фланца 9 с корпусом 2 винтами 14 (резьба М8) Необходимые для вычерчивания винта размеры находим в ГОСТ 1491-80: Винты с цилиндрической головкой классов... номинальный диаметр резьбы d=8 мм; крупный шаг резьбы 1,25 мм; диаметр головки D=13 мм; высота головки k=5 мм; длина резьбы b=26 мм; Здесь при вычерчивании резьбового отверстия в корпусе необходимо воспользоваться данными ГОСТ 10549-80: Выход резьбы. Сбеги, недорезы, проточки... Чтобы определить параметры: сбег x = 3,3 мм; недорез a = 5 мм. III – соединена втулка сальника 4 с корпусом 2 шпильками 20 (резьба М10, материал корпуса – чугун), установлены пружинные шайбы 18 и гайки 15 Необходимые данные (конструкция и размеры шпильки) для построения ее изображения находим в ГОСТ 22034-76 номинальный диаметр резьбы d=8 мм; крупный шаг резьбы 1,5 мм; диаметр стержня 10 мм; длина ввинчиваемого конца 12 мм; длина гаечного конца 30 мм; IV – закреплен маховик 5 на шпинделе 3 установочным винтом 13 (резьба М6) Необходимые данные (конструкция и размеры) для построения его изображения находим в ГОСТ 1476-93; V – выполнено соединение шпинделя 3 и втулки маховика 5 шпонкой 21 (размеры шпонки 6х6х25) Необходимые для построения его изображения находим в ГОСТ 23360-78: Основные нормы взаимозаменяемости. Настоящий стандарт распространяется на шпоночные соединения с призматическими шпонками и устанавливает размеры и предельные отклонения размеров призматических шпонок и соответствующих им шпоночных пазов на валах и во втулках Для вала диаметром 17 мм установлена шпонка сечением 5×5 мм и ее длина может составлять от 10 до 55 мм. Принимаем длину шпонки 25 мм; VII – подсоединить к корпусу 2 угольник 17 (резьба G 3/4.) Необходимые для построения его изображения находим в ГОСТ 8946-75. Настоящий стандарт распространяется на проходные угольники с углом 90 град. и 45 град. из ковкого чугуна с цилиндрической резьбой для трубопроводов. Конструктивные размеры по ГОСТ 8944-75; Выполнить резьбовые соединения деталей сборочного чертежа с их упрощенным изображением по ГОСТ 2.315-68
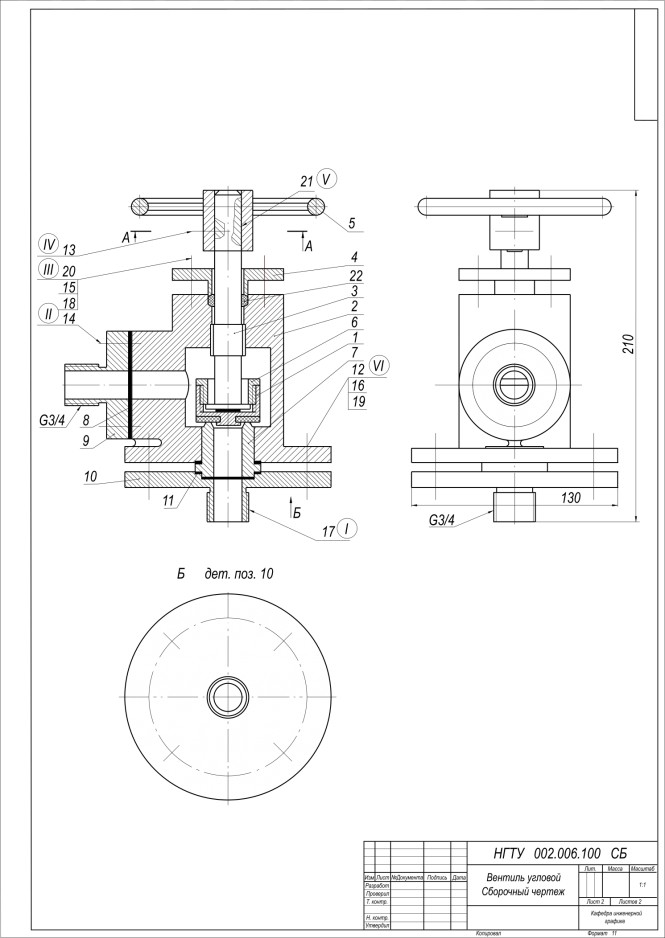
Теперь имея чертеж, можно продолжить выполнение задания. КомментарииВыполнить резьбовые соединения деталей сборочного чертежа с их упрощенным изображением по ГОСТ 2.315-68
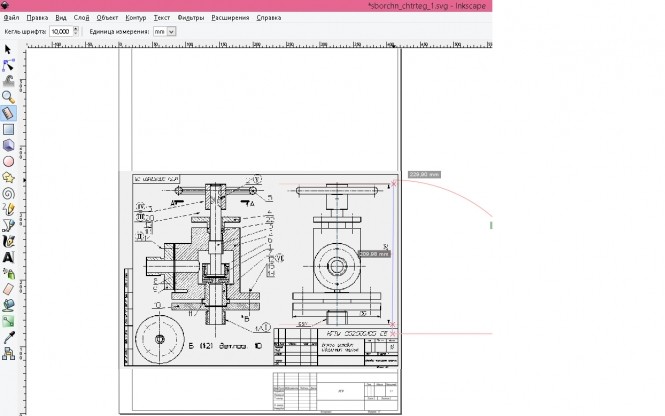
Создание чертежа «свтокопированием» в Inkscape. 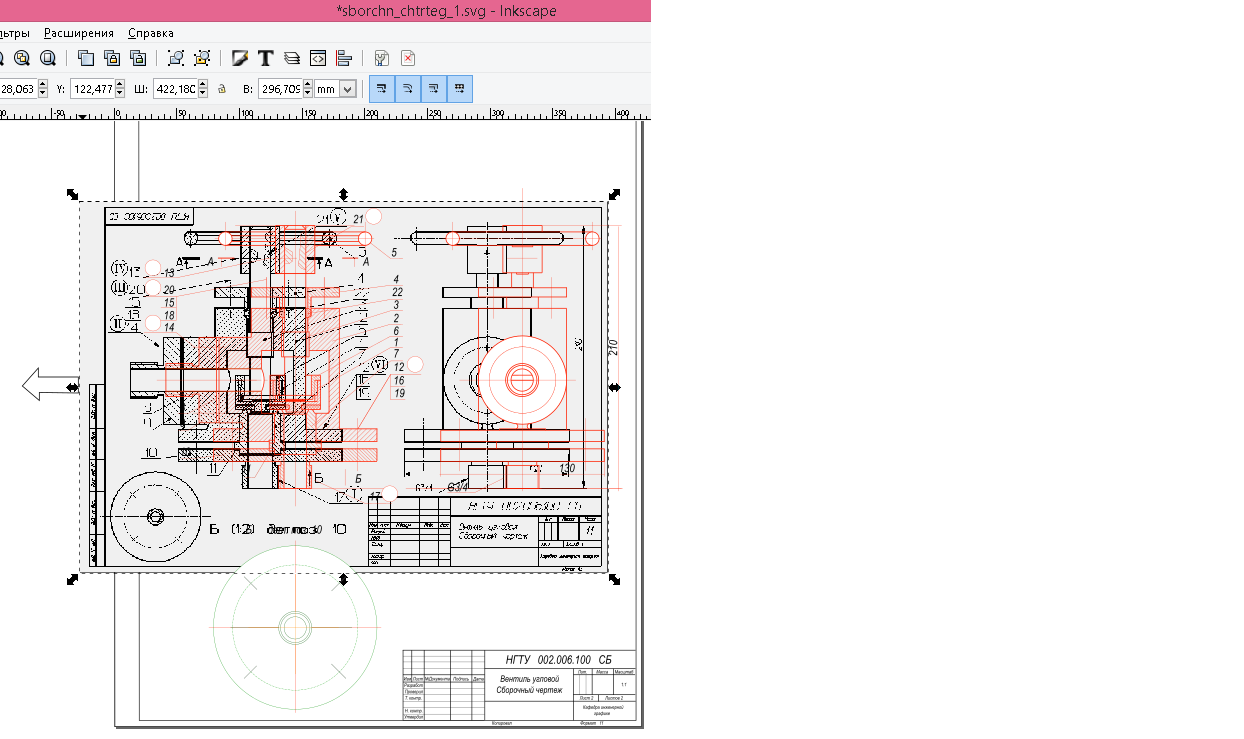
рисунок 1 На рисунке показано вытаскивание оригинала после окончания «свтокопирования». КомментарииВыполнить резьбовые соединения деталей сборочного чертежа с их упрощенным изображением по ГОСТ 2.315-68
Начало работы со сборочным чертежем в Inscape КомментарииСпособом замены плоскостей построить сечение плоскостью общего положения и натуральную величину сечения
Вижу вы стали чертить на бумаге. Надеюсь вы вернетесь к освоению Inkscape позднее. На вашем рисунке пока все верно. Вы создали несколько пустых решений на странице, заполните их а то не могу отправить вам свой комментарий. Повторяю их на Inkscape Напишите как будете строить проекцию (точек) на новой плоскости проекций, а я нарисую. КомментарииСпособом замены плоскостей построить сечение плоскостью общего положения и натуральную величину сечения
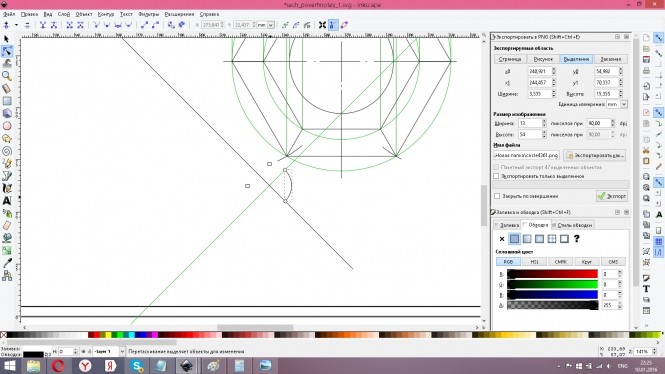
Продолжаем знакомится с инструментами Инкскейп: измерительная линейка. Здесь для удобства работы тонкие линии чертежа должны быть 0,2 мм. Измерение расстояния между двумя параллельными линиями производим перечеркиванием их в перпендикулярном направлении. Измерительная линейка 1 Данное расстояние на чертеже должно быть 15 мм. Чтобы его достигнуть надо одну из линий отодвинуть. Для этого выполняем клонирование отодвигаемой линии и перемещаем ее одним нажатием стрелки на расстояние 0,56 мм. Получаем 14,77 + 0,56 = 15,33. Затем новую линию перетаскиваем немного к старойна величину равную 15,33 - 0,1 -0,1 Желтая линия находится на расстоянии 14,77 + 0,36 = 15,13 Остается убрать еще 0,13 мм перетаскиванием зеленой линии на «глазок». Удаляем старую (черная) и желтую линию и проверяем размер. Достижение размера с точностью до 0,05 мм очень хороший результат. Если допустить построения с меньшей точностью например 0,1 то создание чертежа будет происходить быстрее. 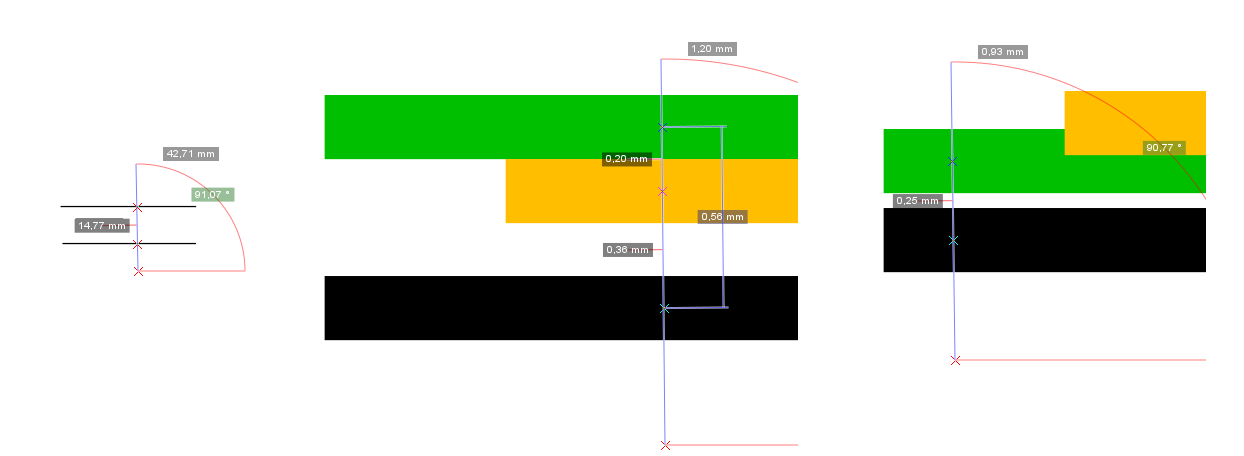
рисунок 1 После полного завершения чертежа выполняем его сохранение как фотографии с расширением .png . Для этого после обычного сохранения ctrl s, в меню файл выбираем Экспортировать в PNG. Откроется соответствующее диалоговое окно где нужно выбрать или указать экспортируемую область: рисунок или выделение. Задаем имя через Экспортировать как и нажимаем кнопку Экспорт. Затем находим в проводнике этот файл открываем его для просмотра, чтобы удостовериться что получили то что хотели. Файл с расширением .png размещаем в решении задачи. Вижу вы стали чертить на бумаге. Надеюсь вы вернетесь к освоению Inkscape позднее. На вашем рисунке пока все верно. Вы создали несколько пустых решений на странице, заполните их а то не могу отправить вам свой комментарий. КомментарииСпособом замены плоскостей построить сечение плоскостью общего положения и натуральную величину сечения
Работая в таком режиме дублирование и перетаскивание получаем на чертеже все тонкие линии одной толщины и основные линии одной толщины. Окружность также создается один раз и в последующем дублируется и перетаскивается Чтобы задать окружность с центром например в пересечении линий необходимо удерживать Shift при перемещении инструмента. Получится эллипс который исправляем в круг удерживая ctrl и перетаскивая квадратный узел. 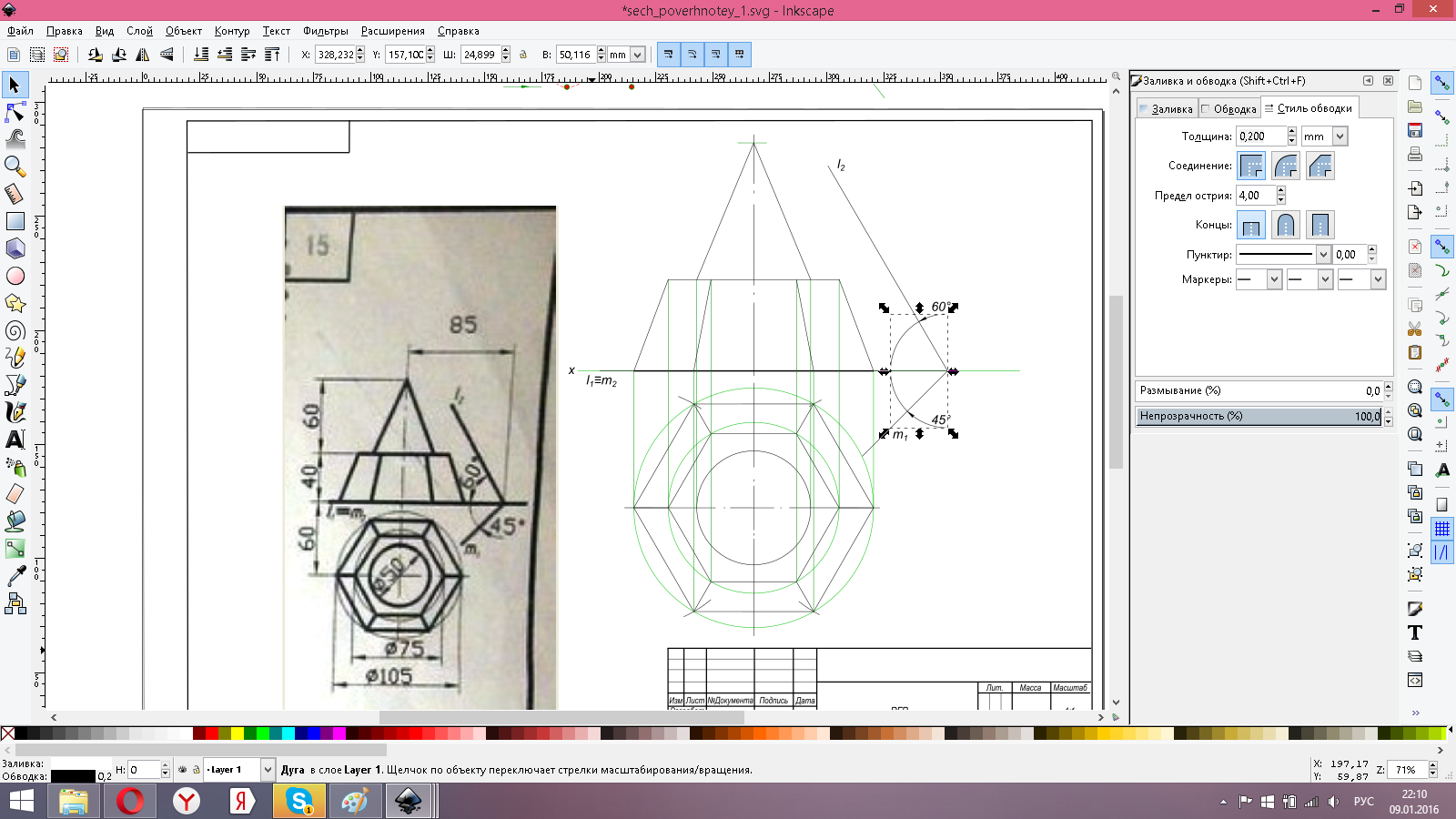
рисунок 2 Переключатель языка рус англ держите в положении англ. из-за этого не работает дублирование. Дуга окружности получается если выделить объект указателем мыши F2 и потянуть за узел-кружок на линии окружности. Окружность можно также повернуть, при этом повернутся ее узлы. Окружность непрозрачна и закрывает другие объекты, здесь надо работать слоями или заменить целый круг некоторым количеством неполных окружностей. По правому краю окна программы расположены пиктограммы прилипания. Некоторые из них необходимо включить, смотрите рисунок. Холст можно приближать и отдалять клавишами плюс и минус или вращением колеса мыши если ее указатель намести на окошечко масштаба внизу и справа. Холст можно перемещать влево, вправо и вверх, вниз клавишами ctrl стрелка. Необходимо с некоторой регулярностью выполнять сохранение создаваемого рисунка, чтобы не потерять проделанную работу из-за каких либо сбоев компьютера. В меню правка имеется опция отменить, которой пользуются для отмены каких то неправильно выполненных построений. Можно разобрать все построения до самого начала и затем все восстановить использую опцию вернуть. Данная опция работает в каждом сеансе работы компьютера. Смотрите также http://ngeo.fxyz.ru/графические_работы/выполнение_чертежа_в_графическом_редакторе/чертеж_в_inkscape/ Если будут вопросы, задавайте. КомментарииНАДЕЮСЬ -ПОЛУЧИЛОСЬ! СПАСИБО! Что дальше, вставила задание, а рамка не убирается...
|
Записать новую задачу Все задачи Все темы Все инженеры |


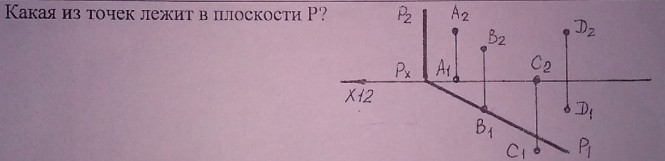



Комментарии