Все решения инженера @NICKНа прямой ab построить точку c на расстоянии 10 мм от точки a
На прямой ab построить точку c на расстоянии 10 мм от точки a 
На прямой ab построить точку c на расстоянии 10 мм от точки a Построить точку в, симметричную точке а относительно прямой mn. а(55,40,25); m(65,5,15); n(5,45,15)
Построить точку в, симметричную точке а относительно прямой mn. а(55,40,25); m(65,5,15); n(5,45,15)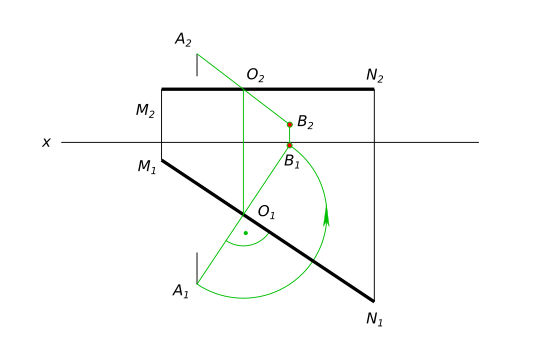 
Построить точку в, симметричную точке а относительно прямой mn. а(55,40,25); m(65,5,15); n(5,45,15) Точка B, симметричная точке A относительно прямой mn, находится на перпендикуляре к данной прямой, исходящем из точки A. Для решения задачи воспользуемся теоремой о проецировании прямого угла КомментарииЗакончить изображение вида сверху. Построить вид слева
Закончить изображение вида сверху. Построить вид слева 
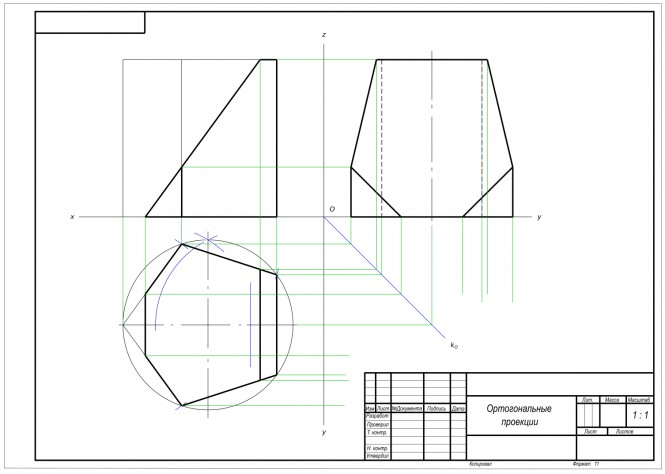
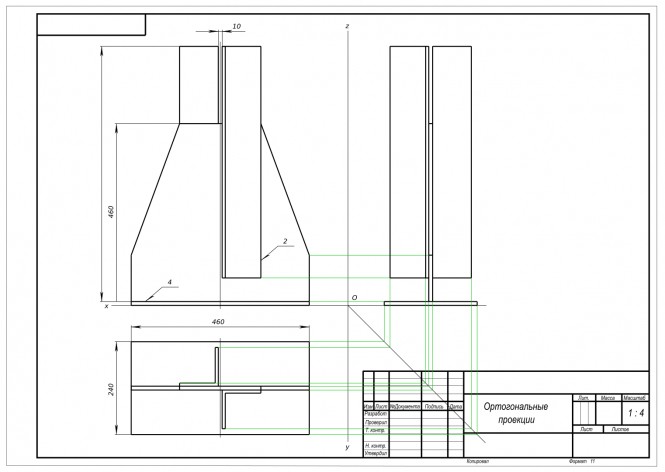
Закончить изображение вида сверху. Построить вид слева Построение правильного пятиугольника с помощью циркуля выделено синим цветом По двум заданным проекциям точек построить их третьи проекции на эпюре
По двум заданным проекциям точек построить их третьи проекции на эпюре 
По двум заданным проекциям точек построить их третьи проекции на эпюре КомментарииПостроить проекцию точек B и C равноудаленных от плоскостей п1 и п2 и конкурирующих с заданними точками A и D. Точка B конкурирует с точкой A относительно п1 точка C конкурирует с точкой D относительно п2.
Построить проекцию точек B и C равноудаленных от плоскостей п1 и п2 и конкурирующих с заданными точками A и D. Точка B конкурирует с точкой A относительно п1 точка C конкурирует с точкой D относительно п2.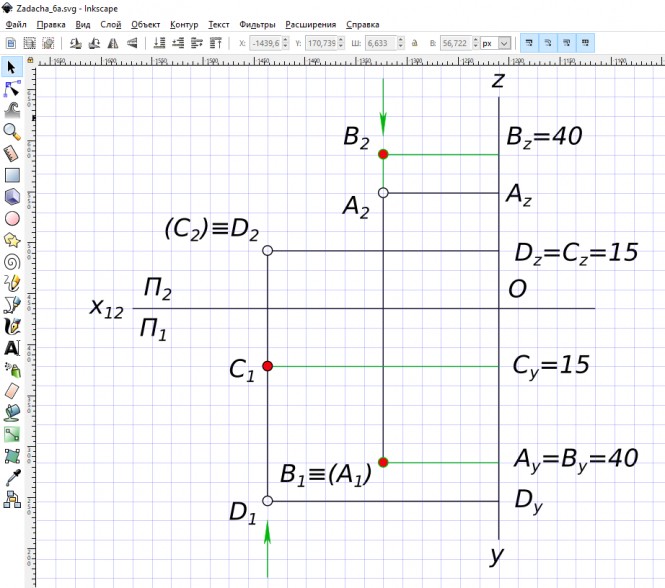 
Построить проекцию точек B и C равноудаленных от плоскостей п1 и п2 и конкурирующих с заданными точками A и D. Точка B конкурирует с точкой A относительно п1 точка C конкурирует с точкой D относительно п2. КомментарииДана точка а (30, 40, 30). построить проекции точек в, с, d, симметричных точке а относительно осей ox, oy, oz соответственно.
Дана точка а (30, 40, 30). построить проекции точек в, с, d, симметричных точке а относительно осей ox, oy, oz соответственно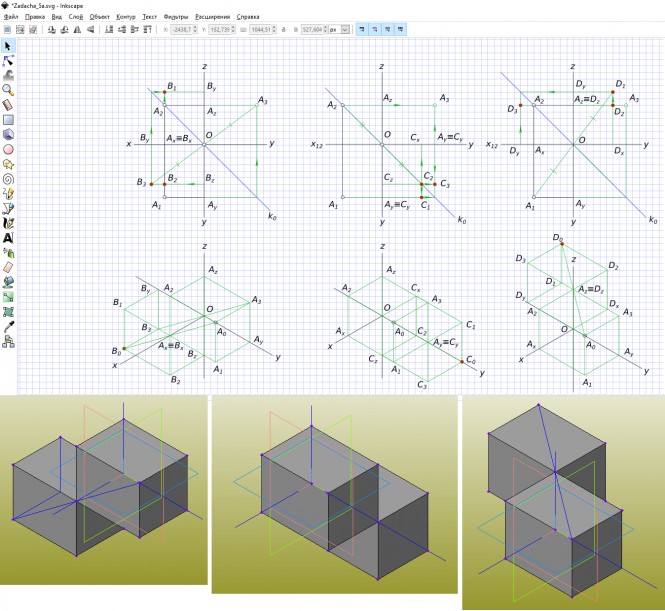 
Дана точка а (30, 40, 30). построить проекции точек в, с, d, симметричных точке а относительно осей ox, oy, oz соответственно Точки B, C, D, симметричные точке A относительно осей ox, oy, oz соответственно находятся на перпендикулярах проведенных из заданной точки к ним. Решение: 1. Точа B находится на перпендикуляре к оси Ox, на одинаковом с точкой A удалении от нее |OA3|=|OB3|. 2. Ax≡Bx, находим Bz и затем B2, находим By и затем B1. 3. B(30,-40,-30) Решение: 1. Точа B находится на перпендикуляре к оси Oy, на одинаковом с точкой A удалении от нее |OA2|=|OC2|. 2. Ay≡Cy, находим Cx и затем C1, находим Cz и затем C3. 3. C(-30,40,-30) Решение: 1. Точа D находится на перпендикуляре к оси Oz, на одинаковом с точкой A удалении от нее |OA1|=|OD1|. 2. Az≡Bz, находим Dx и затем D2, находим Dy и затем D3. 3. D(-30,-40,30) КомментарииПостроить проекции точек b, c, d симметричных точке a 15.25.30 относительно плоскостей П1, П2, П3 соответственно.
Построить проекции точек b, c, d симметричных точке a 15.25.30 относительно плоскостей П1, П2, П3 соответственно. Чтобы выполнить построение необходимо знать условие симметричности точек относительно π1, π2 и π3 
Построить проекции точек b, c, d симметричных точке a 15.25.30 относительно плоскостей П1, П2, П3 соответственно По условию задачи точка B симметрична точке A, относительно плоскости π1 откуда следует вывод, что они находятся на перпендикуляре к π1 по разные стороны от нее. Ax=Bx; Ay=By и Bz=-Az По условию задачи точка C симметрична точке A, относительно плоскости π2 откуда следует вывод, что они находятся на перпендикуляре к π2 по разные стороны от нее. Ax=Cx; Cy=-Ay и Cz=Az По условию задачи точка D симметрична точке A, относительно плоскости π3 откуда следует вывод, что они находятся на перпендикуляре к π3 по разные стороны от нее. Dx=-Ax; Dy=Ay и Dz=Az КомментарииПостроить множество точек равноудаленных от сторон угла
Построить множество точек равноудаленных от сторон угла 
Построить множество точек равноудаленных от сторон угла КомментарииПостроить множество точек плоскости удаленных на заданную величину r от окружности n
Построить множество точек плоскости удаленных на заданную величину r от окружности n 
Построить множество точек плоскости удаленных на заданную величину r от окружности n КомментарииПостроить множество точек плоскости, удаленных на заданную величину от прямой
Построить множество точек плоскости α, удаленных на заданную величину от прямой m(m1, m2) 
Построить множество точек плоскости, удаленных на заданную величину от прямой КомментарииНастроить электронные часы
Настроить электронные часы iTaiTek IT-915 
Настроить электронные часы button functions - функции кнопок Mode - selecting button - кнопка выбора Start - adjusting button - кнопка репулировки Reset - shift button - кнопка Shift Light - Cold Light button - Кнопка подсветки Для настройки электронных наручных часов iTaiTek IT-915 применяются три красные кнопки - Mode, Start и Reset. Представим, что электронные наручные часы - компьютер. Здесь пользователь может поочередно работать в окнах (программах) - "секундомер", "будильник" и "часы" Штатный режим работы часов Алгоритм настройки Открываем окно секундомера Mode^{1-ое нажатие} Здесь ничего не требуется редактировать. Открываем окно будильника и редактируем время срабатывания Mode^{2-ое нажатие} Reset^{1-ое нажатие}(выставляем часы) Start Reset^{2-ое нажатие}(выставляем минуты) Start (редактируем дни недели срабатывния сигнала) Reset^{3-ое нажатие}(выставляем дни недели срабатывния сигнала) Start Reset^{4-ое нажатие}(выставляем для сигнала положение вкл/выкл) Start Открываем окно часов и редактируем время, дату и день недели) Mode^{3-е нажатие} Reset^{1-ое нажатие}(выставляем часы) Start Reset^{2-ое нажатие}(выставляем минуты) Start (редактируем показания календаря в формате месяц число) Reset^{3-е нажатие}(выставляем число) Start Reset^{4-ое нажатие}(выставляем месяц) Start (редактируем день недели) Reset^{5-ое нажатие}(выставляем день недели) Start Mode^{4-е нажатие} Завершаем настройку Штатный режим работы часов КомментарииПостроить проекции прямого кругового конуса
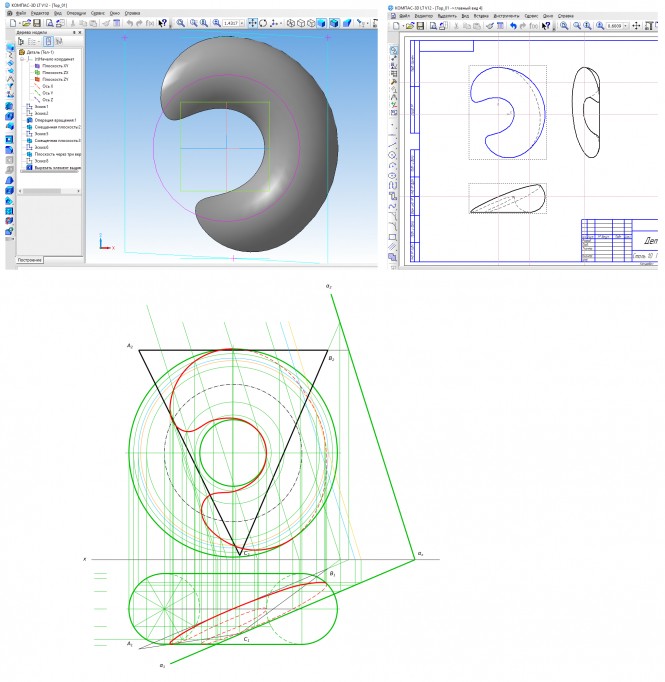
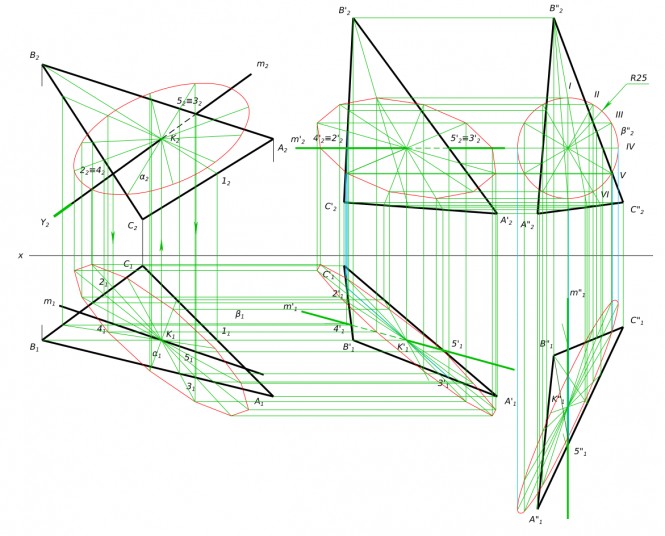
Построить проекции прямого кругового конуса, если его ось лежит на прямой MN, а точка A(A1, A2) лежит на окружности основания и угол между образующими и основанием равен 60°. 
Построить проекции прямого кругового конуса КомментарииПостроение перспективы методом архитектора . Построение теней на перспективе
Построение перспективы методом архитектора . Построение теней на перспективе 
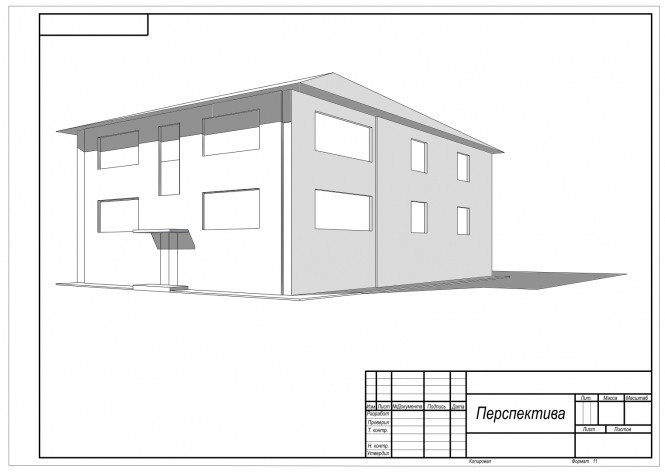
Построение перспективы методом архитектора . Построение теней на перспективе КомментарииПостроить равнобедренный треугольник
Построить равнобедренный треугольник ABC с основанием BC на прямой MN исходя из условия, что угол при основании равен 30 градусам.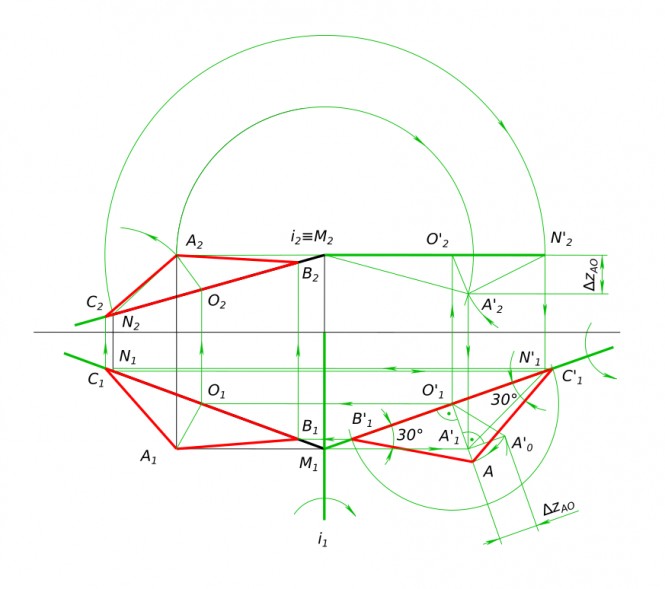 
Построить равнобедренный треугольник ABC с основанием BC на прямой MN исходя из условия, что угол при основании равен 30 градусам. КомментарииПровести прямую параллельную данной прямой
Провести прямую параллельную данной прямой. Интервал прямой определить графически и аналитически.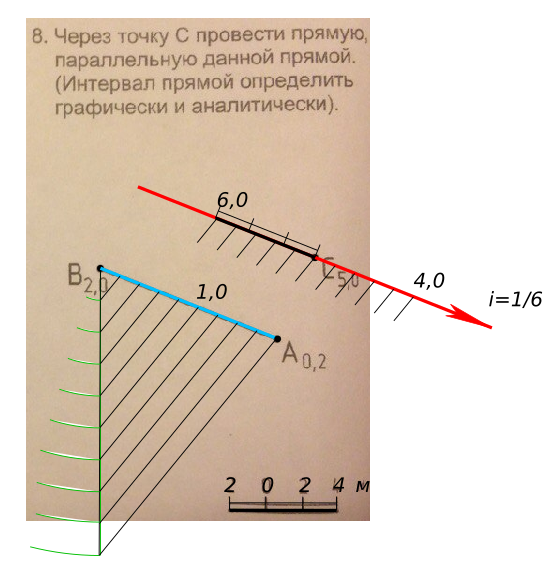 
Провести прямую параллельную данной прямой. Интервал прямой определить графически и аналитически. КомментарииРаспределение напряжений по сечению балки при изгибе
Распределение напряжений по сечению балки при изгибе Зная распределение нормальных напряжений по поперечному сечению балки, можно доказать, что прямой чистый изгиб возможен, только тогда когда плоскость внутреннего изгибающего момента совпадает совпадает с одной из главных центральных осей. То есть, совпадает с одной из главных плоскостей поперечного сечения.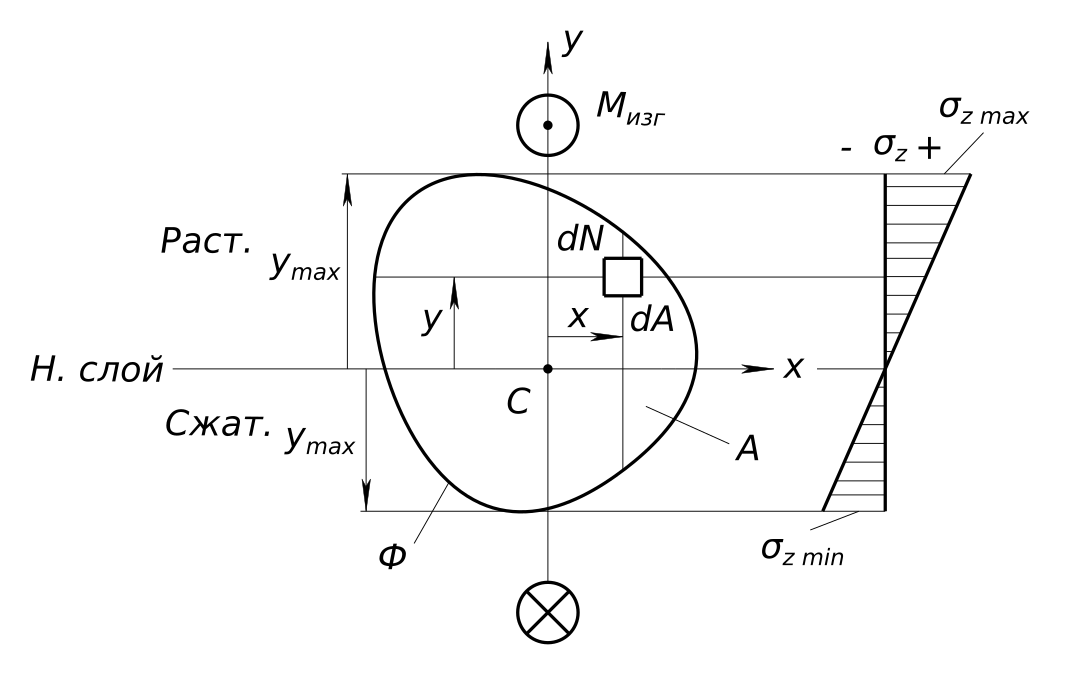 
Распределение напряжений по сечению балки при изгибе Внутренний изгибающий момент действует в плоскости какой-то оси y. Этот изгибающий момент стремится изогнуть балку таким образом, чтобы нормальные напряжения в поперечном сечении распределялись по линейному закону.
$ M_{x}=M_{изг} $ Точки оси балки будут изгибаться в плоскости zy , только тогда когда
$ M_{y}=0=\int\from{Ф}xdN=\int\from{A}xσdA=\int\from{A}\frac{M_{x}}{J_{x}}xydA=\frac{M_{x}}{J_{x}}\int\from{A}xydA $ Где центробежный момент инерции
$ \int\from{A}xydA=J_{xy} $ Тогда
$ M_{y}=\frac{M_{x}}{J_{x}}J_{xy} $ Чтобы изгиб был прямым центробежный момент инерции приравниваем к нулю
$ J_{xy}=0 $ Данное равенство означает что оси x и y - это главные оси, пересекающиеся в центре тяжести поперечного сечения. Значит прямой чистый изгиб возможен, только тогда когда плоскость внутреннего изгибающего момента совпадает совпадает с одной из главных центральных осей. То есть, совпадает с одной из главных плоскостей поперечного сечения КомментарииРаспределение напряжений по сечению балки при изгибе
Зная нормальное напряжение σ_{z} в любом отдельно взятом слое, можем вычислить внутренний изгибающий момент, действующий в каждом из сечений 
Распределение напряжений по сечению балки при изгибе Здесь y - главная центральная ось. Изгиб происходит в главной плоскости yz. Ось x проходит через нейтральный слой. Сила действующая на элементарную площадку dA равна
$ dN=σdA=E\frac{y}{ρ}dA $ Тогда
$ M_{x}=\int\from{Ф}ydN=\int\from{A}E\frac{y}{ρ}ydA=\frac{E}{ρ}\int\from{A}y^{2}dA=\frac{E}{ρ}J_{x} $ Откуда находим кривизну оси изогнутого стержня в каком-либо поперечном сечении
$ \frac{1}{ρ}=\frac{M_{x}}{EJ_{x}} $ Тогда
$ σ_{z}=Ey\frac{1}{ρ}=Ey\frac{M_{x}}{EJ_{x}}=\frac{M_{x}}{J_{x}}y $ Или
$ σ_{max}=\frac{M_{x}}{W_{x}} $ где W_{x} - момент сопротивления при изгибе Откуда
$ W_{x}=\frac{J_{x}}{y_{max}} $ Для расчетов необходимы максимальные по модулю напряжения, поэтому в поперечном сечении берется точка наиболее удаленная от нейтрального слоя. Тогда
$ N=0=\int\from{Ф}dN=\int\from{A}σdA=\int\from{A}\frac{M_{x}}{J_{x}}ydA=\frac{M_{x}}{J_{x}}\int\from{A}ydA=\frac{M_{x}}{J_{x}}S_{x} $ Где статический момент сечения относительно оси x равен
$ S_{x} = \int\from{A}ydA $ Анализируя данное уравнение, приходим к выводу
$ S_{x}=0=y_{C}A $ И тогда - ордината центра тяжести равна нулю, в принятой системе координат
$ y_{C}=0 $ Таким образом, при изгибе ось x проходит через центр тяжести поперечного сечения и является главной центральной осью, также ее называют осью изгиба. КомментарииРаспределение напряжений по сечению балки при изгибе
Распределение напряжений по сечению балки при изгибе 
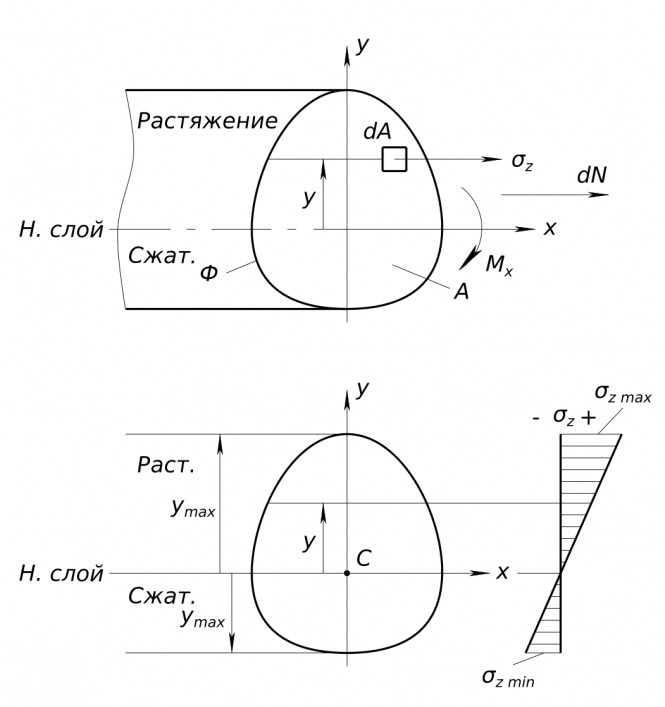
Распределение напряжений по сечению балки при изгибе Рассмотрим кусок балки между двумя плоскими сечениями 1 и 2. До нагружения балка была прямой, после нагружения она изогнута. При этом ее верхние слои подвергаются растяжению, а нижние - сжатию. Зону растянутых слоев отделяет от зоны сжатых слоев нейтральный слой. Допустим кусок балки изогнут по дуге окружности. Вводим систему координат xyz. Тогда, согласно закону Гука для однородного напряженного состояния
$ σ_{z}=EƐ_{z} $ Где Ɛ_{z} - удлинение слоя, удаленного от нейтрального на расстояние y. Допустим, что расстояние между сечениями 1 и 2 бесконечно мало и равно dz. Тогда
$ Ɛ_{AB}=\lim\from{B→A}\frac{∆S}{S} $ В соответствии с гипотезой о плоских сечениях, после нагружения балки получаем, что эти сечения оставшись плоскими повернулись на какой-то угол и угол между ними стал dα. По гипотезе о не надавливании слоев напряжения поперек оси отсутствуют, поэтому расстояние y не изменилось после нагружения балки. Тогда
$ dz=dαρ=AB $ Где ρ - радиус кривизны нейтрального слоя И
$ A'B'=dα(ρ+y) $ Тогда, линейная деформация слоя «y» равна
$ Ɛ_{z}=\frac{A'B'-AB}{AB}=\frac{(ρ+y)dα-ρdα}{dαρ}=\frac{y}{ρ} $ И осевое (нормальное) напряжение в слое «y» равно
$ σ_{z}=EƐ_{z}=E\frac{y}{ρ} $ КомментарииПостроить эпюры поперечных сил Q и изгибающих моментов M
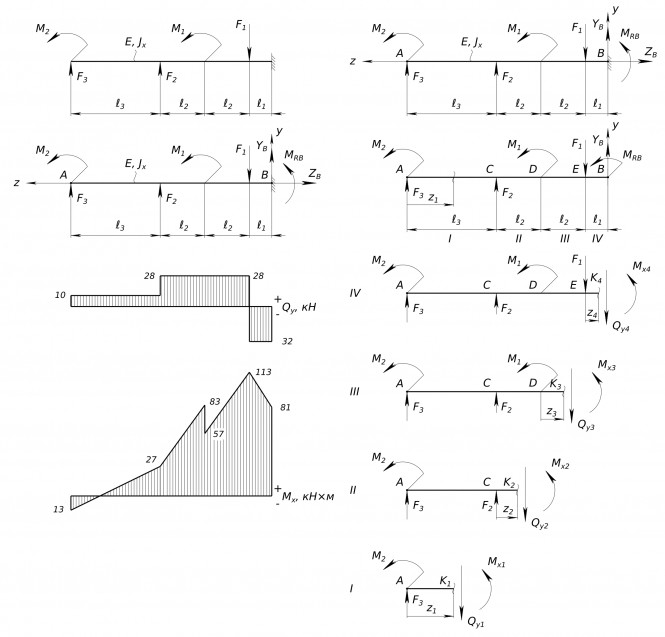
Построить эпюры поперечных сил и изгибающих моментов Участок III. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{3} равна нулю
$ ΣF_{y_{3}}=0=F_{3}+F{2}-Q_{y_{3}} $ тогда
$ Q_{y_{3}}=F_{3}+F_{2}=10+18=28 кН $ Сумма всех моментов относительно точки K_{3} равна нулю
$ ΣM_{K_{3}}=0=M_{x_{3}}+M_{2}+M_{1}-F_{3}(ℓ_{3}+ℓ_{2}+z_{3})-F_{2}(ℓ_{2}+z_{3}) $ тогда
$ M_{x_{3}}=F_{3}(ℓ_{3}+ℓ_{2}+z_{3})+F_{2}(ℓ_{2}+z_{3})-M_{2}-M_{1}= $
$ =10(4+2+z_{3})+18(2+z_{3})-13-26 $ В точке D
$ z_{3}=0; M_{x_{3}}=10(4+2)+18(2+0)-13-26=57 кН×м $ В точке E: z_{3}=ℓ_{2}=2
$ M_{x_{3}}=10(4+2+2)+18*(2+2)-13-26=113 кН×м $ Участок IV. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{4} равна нулю
$ ΣF_{y_{4}}=0=F_{3}+F{2}-F{1}-Q_{y_{4}} $ тогда
$ Q_{y_{3}}=F_{3}+F_{2}-F{1}=10+18-60=-32 кН $ Сумма всех моментов относительно точки K_{4} равна нулю
$ ΣM_{K_{4}}=0 $ или
$ M_{x_{4}}+M_{2}+M_{1}+M_{RB}-F_{3}(ℓ_{3}+2ℓ_{2}+z_{4})-F_{2}(2ℓ_{2}+z_{4})+F_{1}z_{4}=0 $ тогда
$ M_{x_{4}}=F_{3}(ℓ_{3}+2ℓ_{2}+z_{4})+F_{2}(2ℓ_{2}+z_{4})-F_{1}z_{4}-M_{2}-M_{1}= $
$ =10(4+2*2+z_{4})+18(2*2+z_{4})-60z_{4}-13-26 $ В точке E
$ z_{4}=0 $
$ M_{x_{4}}=10(4+2*2+0)+18(2*2+0)-60*0-13-26= $
$ 80+72-0-39=113 кН×м $ В точке B
$ z_{4}=ℓ_{2}=2 $ и
$ M_{x_{4}}= $
$ =10(4+2*2+1)+18*(2*2+1)-60*1-13-26-M_{RB} $
$ =90+90-60-39-81=113 кН×м $ Строить эпюры поперечных сил и изгибающих моментов, используя полученные данные КомментарииПостроить эпюры поперечных сил Q и изгибающих моментов M
Построить эпюры поперечных сил Q и изгибающих моментов M Стержень работающий на изгиб называется балкой. Балка заделанная с одного конца называется консоль. Составляем расчетную схему балки 
Построить эпюры поперечных сил Q и изгибающих моментов M Для решения задачи вводим систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки внешними усилиями: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{A} - горизонтальная реакция Y_{A} - вертикальная реакция M_{RA} - угловая реакция (моментная реакция) Находим реакции, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю:
$ ΣF_{y}=Y_{B}+F_{3}+F_{2}-F_{1}=0 $ Из него находим
$ Y_{B}=F_{1}-F_{3}-F_{2}=60-18-10=32 кН$ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю:
$ ΣF_{z}=-Z_{B}=0 $ Из него находим
$ Z_{B}=0 $ Третье уравнение - сумма всех моментов относительно точки B равна нулю. Плечи Y_{B} и Z_{B} равны нулю
$ ΣM_{B}=M_{RB}+M_{2}+M_{1}-F_{3}(ℓ_{3}+2ℓ_{2}+ℓ_{1})-F_{2}(2ℓ_{2}+ℓ_{1})+F_{1}ℓ_{1}=0 $ из него получаем
$ M_{RB}=F_{3}(ℓ_{3}+2ℓ_{2}+ℓ_{1})+F_{2}(2ℓ_{2}+ℓ_{1})-F_{1}ℓ_{1}-M_{2}-M_{1}= $
$ =81 кН×м $ Четвертое уравнение проверочное - сумма всех моментов относительно точки A равна нулю
$ ΣM_{A}=0=M_{2}+M_{1}+M_{RB}+F_{2}ℓ_{1}-F_{1}(ℓ_{3}+2ℓ_{2})+Y_{B}(ℓ_{3}+2ℓ_{2}+ℓ_{1}) $ из него получаем
$ M_{RB}=F_{1}(ℓ_{3}+2ℓ_{2})-M_{2}-M_{1}-M_{RB}-F_{2}ℓ_{1}-Y_{B}(ℓ_{3}+2ℓ_{2}+ℓ_{1})= $
$ =81 кН×м $ Рисуем силовую схему. Далее разбиваем стержень на участки. Границами участков служат места включения нагрузок. Изменения геометрии сечения балки нет. Получаем четыре участка. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезаем балку, отбрасываем левую часть. Заменяем действие отброшенной части силовыми факторами - Q_{y1}, M_{x1}. Пока не знаем их величину, но рисуем их в положительных направлениях, согласно установленному правилу знаков. Участок I. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{1} равна нулю
$ ΣF_{y_{1}}=0=F_{3}-Q_{y_{1}} $ тогда
$ Q_{y_{1}}=F_{3}= 10 кН $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=M_{x_{1}}+M_{2}-F_{3}z_{1} $ тогда
$ M_{x_{1}}=F_{3}z_{1}-M_{2} $ В точке A
$ z_{1}=0; M_{x_{1}}=-13 кН×м $ В точке C
$ z_{1}=ℓ_{3}; M_{x_{1}}=F_{3}ℓ_{3}-M_{2}=10*4-13=27 кН×м $ Участок II. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{2} равна нулю
$ ΣF_{y_{2}}=0=F_{3}+F{2}-Q_{y_{2}} $ тогда
$ Q_{y_{2}}=F_{3}+F_{2}=10+18=28 кН $ Сумма всех моментов относительно точки K_{2} равна нулю
$ ΣM_{K_{2}}=0=M_{x_{2}}+M_{2}-F_{3}(ℓ_{3}+z_{2})-F_{2}z_{2} $ тогда
$ M_{x_{2}}=F_{3}(ℓ_{3}+z_{2})+F_{2}z_{2}-M_{2}=10(4+z_{2})+18z_{2}-13 $ В точке C
$ z_{2}=0; M_{x_{2}}=10(4+0)+0-13=27 кН×м $ В точке D
$ z_{2}=ℓ_{2}=2; M_{x_{2}}=10(4+2)+18*2-13=83 кН×м $ КомментарииДана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС. А(70,60,45) В(40,0,55) С (0,45, 10) D (65,15,0)
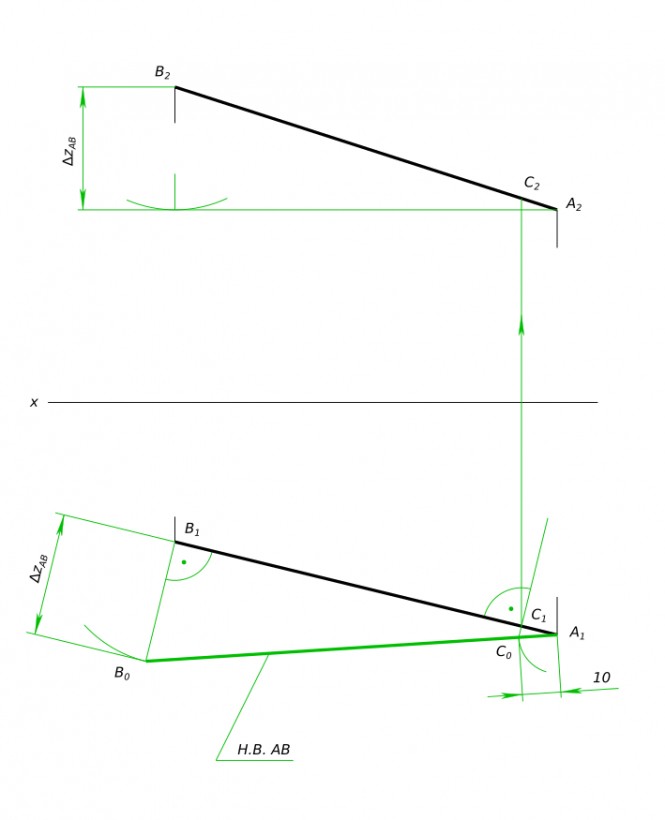
Дана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС способом вращения. А(70,60,45) В(40,0,55) С (0,45, 10) D (65,15,0)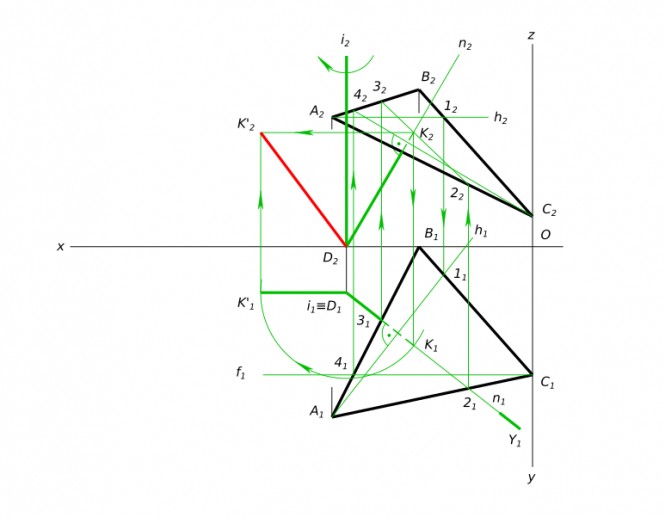 
Дана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС способом вращения КомментарииДана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС. А(70,60,45) В(40,0,55) С (0,45, 10) D (65,15,0)
Дана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС способом вращения. А(70,60,45) В(40,0,55) С (0,45, 10) D (65,15,0) 
Дана плоскость треугольника АВС и точка D. Требуется определить расстояние от точки D до плоскости заданной треугольником АВС способом вращения КомментарииБалка нагруженная силой
Балка нагруженная силой По полученным расчетам строим эпюры внутренних силовых факторов - эпюр перерезывающей силы и эпюр моментов 
Балка нагруженная силой Эпюра перерезывающей силы Q_{y} выше с нулевой линии. В любом сечении перерезывающая сила равна F
$ Q_{y} = F $ Эпюра моментов M_{x} показывает, что момент действующий на участке не постоянный и отрицательный его величина линейно возрастает от конца балки к ее заделке, достигая наибольшего значения равного
$ M_{x} = F ℓ $ Правило знаков при нахождении изгибающих моментов в сечениях балки: Если нижние слои балки растянуты, то найденный момент положительный, если наоборот - отрицательный. КомментарииБалка нагруженная силой
Балка нагруженная силой Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезав балку, отбрасываем левую часть. 
Балка нагруженная силой Заменяем действие отброшенной части силовыми факторами: Q_{y1}, M_{x1}. Пока не знаем их величину, но рисуем их в положительных направлениях, согласно установленному правилу знаков. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{1} равна нулю
$ ΣF_{y_{1}}=0=Q_{y_{1}}-F $ тогда
$ Q_{y_{1}}=F $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=-M_{x_{1}}-Fz_{1} $ тогда
$ M_{x_{1}}=-Fz_{1} $ В точке B
$ z_{1}=0; M_{x_{1}}=-F×0=0 $ В точке A
$ z_{1}=ℓ; M_{x_{1}}=-F ℓ $ Реактивный момент M_{x_{1}} найден со знаком минус. А это означает, что его действительное направление противоположно принятому при составлении уравнения равновесия. Исправляем направление M_{RA} на расчетной схеме. КомментарииБалка нагруженная силой
Балка нагруженная силой Рисуем силовую схему 
Балка нагруженная силой Четвертое (проверочное) уравнение - сумма всех моментов относительно точки B равна нулю.
$ ΣM_{B}=-F ℓ+F ℓ=0 $ Далее разбиваем стержень на участки. Границами участка служат концы балки. Нагрузка приложена к концу балки. Изменения геометрии сечения балки нет. Получаем один участок. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. КомментарииБалка нагруженная силой
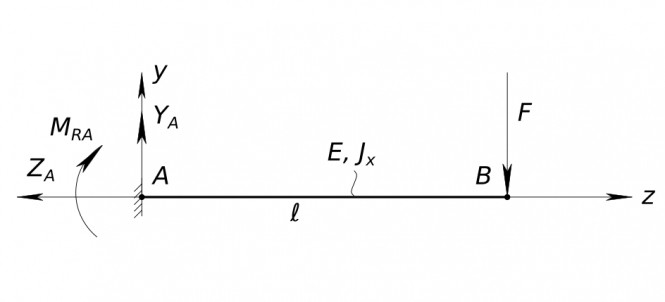
Балка нагруженная силой. Стержень работающий на изгиб называется балкой. Балка заделанная с одного конца называется консоль. Расчетная схема балки 
Балка нагруженная силой ℓ - длина балки Jx - момент инерции относительно главной центральной оси х E - модуль упругости материала балки EJx - изгибная жесткость Стержневая конструкция, все стержни которой лежат в одной плоскости и в этой же плоскости деформируются, называется плоской конструкцией. Для решения задачи вводим систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки силой: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{A} - горизонтальная Y_{A} - вертикальная M_{RA} - угловая (моментная) Находим, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю
$ ΣF_{y}=Y_{A}-F=0 $ из него находим
$ Y_{A}=F $ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю
$ ΣF_{z}=-Z_{A}=0 $ Из него находим Z_{A}=0
$ Z_{A}=0 $ Третье уравнение - сумма всех моментов относительно точки A равна нулю. Момент силы принято считать положительным, если он вращает балку против часовой стрелки и наоборот - если по часовой стрелке. Учитывая, что плечи реакций Y_{A} и Z_{A} равны нулю
$ ΣM_{A}=-M_{RA}-F ℓ=0 $ из него получаем
$ M_{RA}=-F ℓ $ КомментарииДеталь в терх проекциях
Деталь в трех проекциях 
Деталь в трех проекциях КомментарииОпределить угол наклона плоскости к П2
Определить угол наклона плоскости к П2 
Определить угол наклона плоскости к П2 КомментарииБалка нагруженная моментом
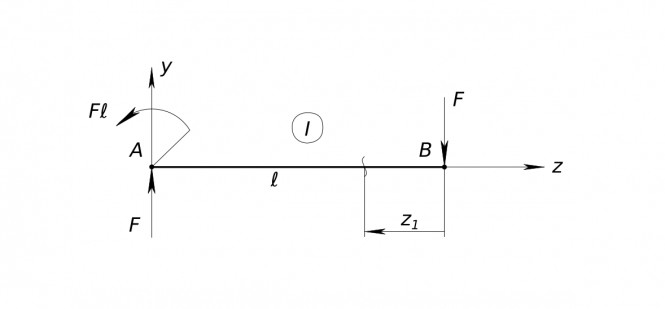
Балка нагруженная моментом По полученным расчетам строим эпюр поперечной силы и эпюр моментов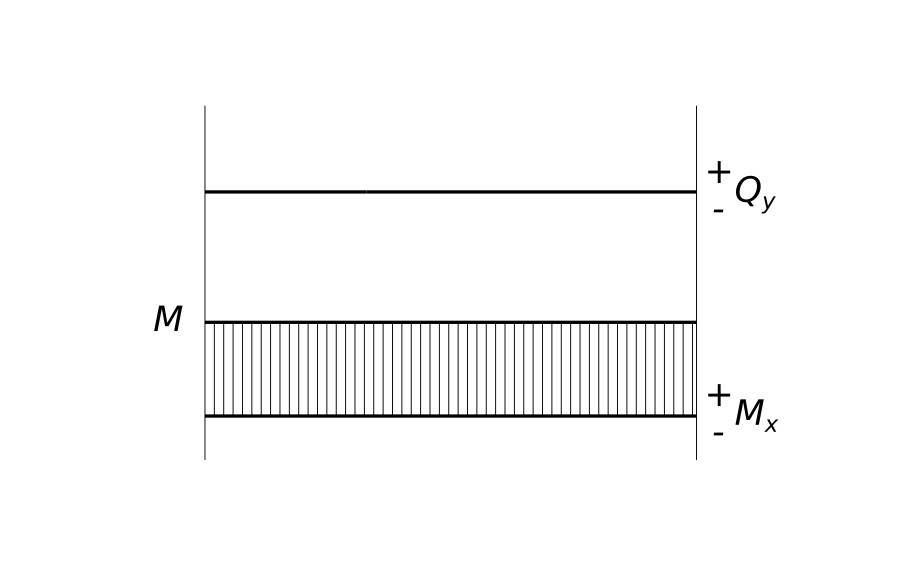 
Балка нагруженная моментом Эпюра перерезывающей силы Q_{Y} совпадает с нулевой линией, потому что ее значение равно нулю
$ Q_{y} = 0 $ Эпюра моментов M_{X} показывает, что момент действующий на участке постоянный и положительный и равен M
$ M_{x} = M $ КомментарииБалка нагруженная моментом
Балка нагруженная моментом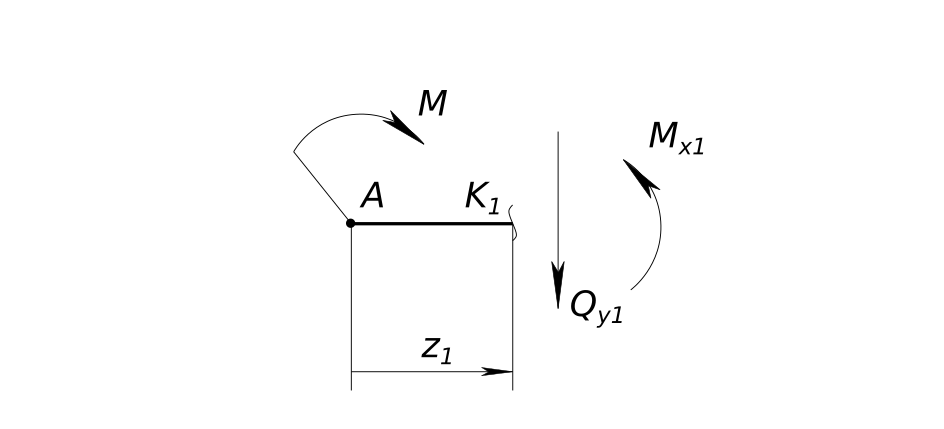 
Балка нагруженная моментом Мысленно разрезаем балку, отбрасываем правую часть. Заменяем действие отброшенной части силовыми факторами - Q_{x_{1}}, M_{x_{1}}. Пока не знаем их величину, но рисуем их в положительных направлениях. Составляем уравнения равновесия Сумма всех сил в проекции на ось Y_{1} равна нулю
$ ΣF_{y_{1}} = 0 $ Вдоль оси y действует только одна сила, это Q_{y_{1}}. Ее направление противоположно направлению оси y1. Поэтому в уравнении она со знаком «минус»
$ -Q_{y_{1}}} = 0 $ Откуда
$ Q_{y_{1}}} = 0 $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=+M_{x_{1}}-M $ Тогда
$ M_{x_{1}}=M $ Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии