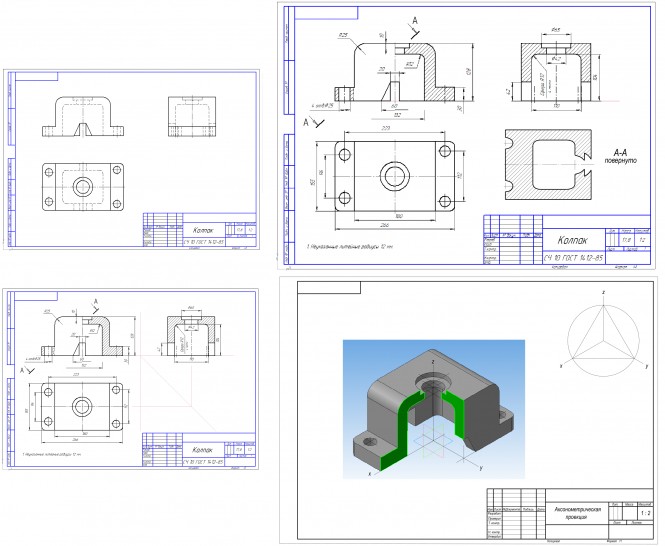
Все решения инженера @NICKПостроить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом
Построить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом 
Построить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом Построить три проекции детали с наклонным сечением; выполнить полезные разрезы, построить диметрию с вырезом части ее
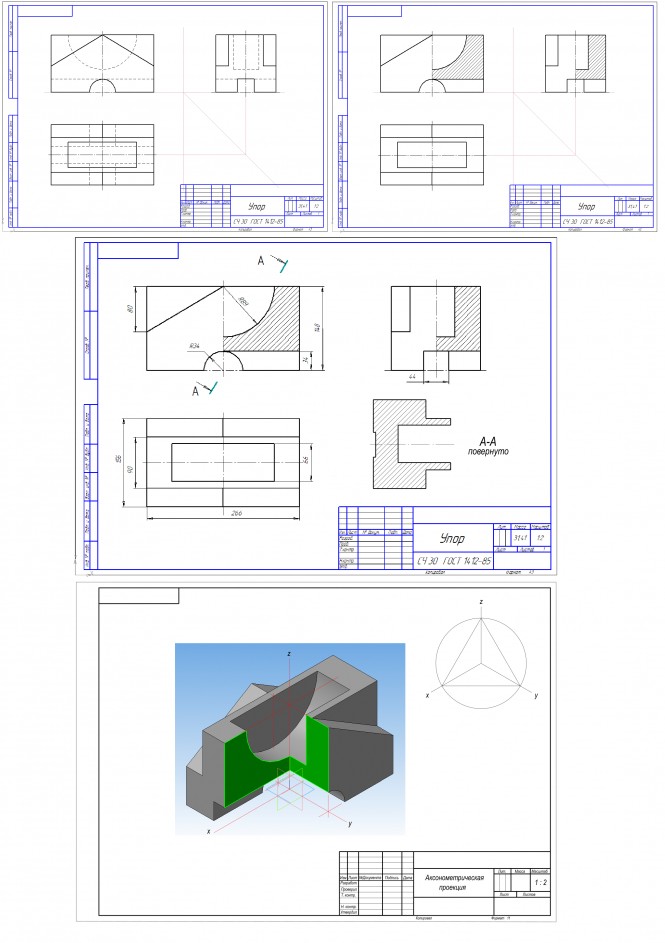
Построить три проекции детали с наклонным сечением; построить прямоугольную диметрию с вырезом части ее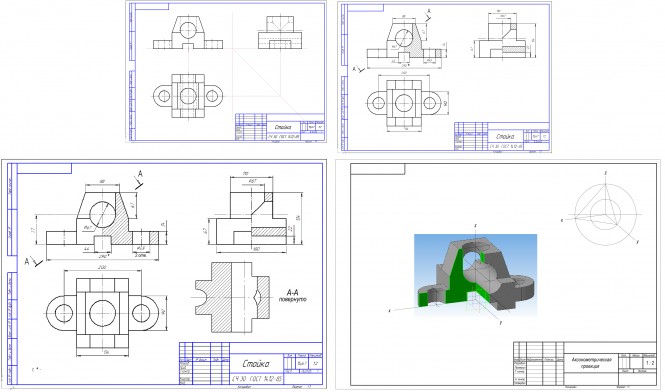 
Построить три проекции детали с наклонным сечением; построить прямоугольную диметрию с вырезом части ее На свободном месте чертежа делаем надпись «1. * - Размеры для справок.» КомментарииПостроить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом
Построить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом 
Построить три проекции детали с сечением; построить прямоугольную изометрию с аксонометрическим вырезом Построить точку A, принадлежащую прямой e и отстоящую от прямой n на 20 мм
Построить точку A, принадлежащую прямой e и отстоящую от прямой n на 20 мм 
Построить точку A, принадлежащую прямой e и отстоящую от прямой n на 20 мм КомментарииПостроить точку N симметричную точке M относительно плоскости ABC
Построить точку N симметричную точке M относительно плоскости ABC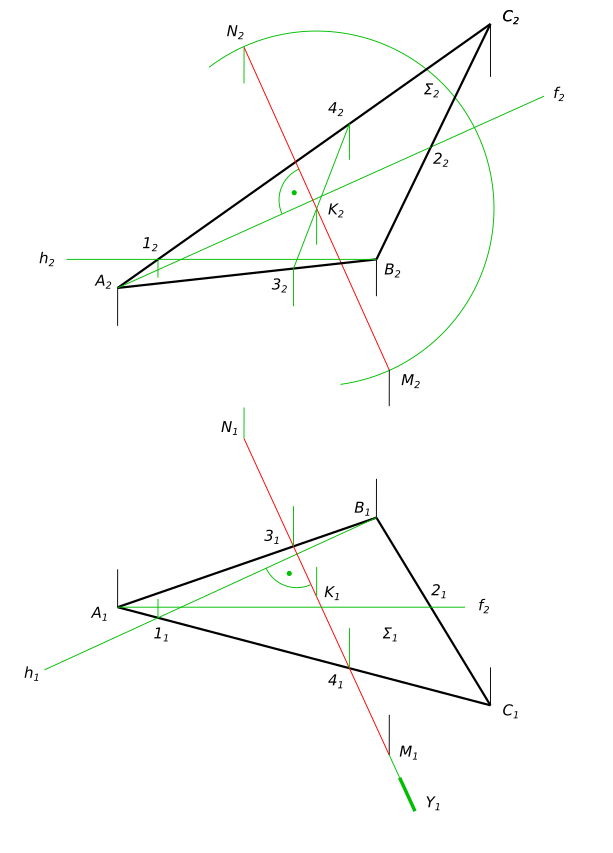 
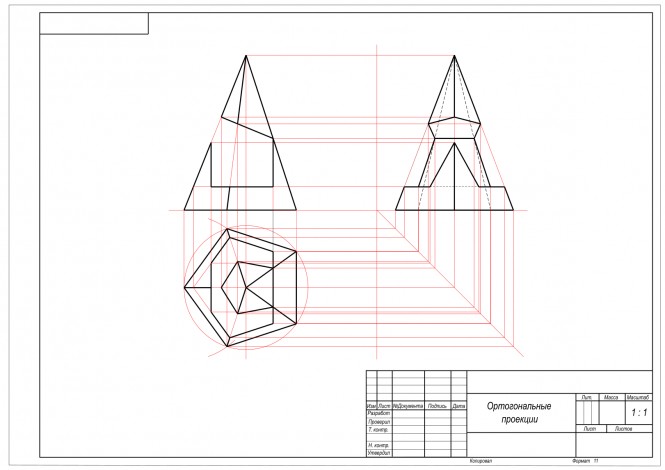
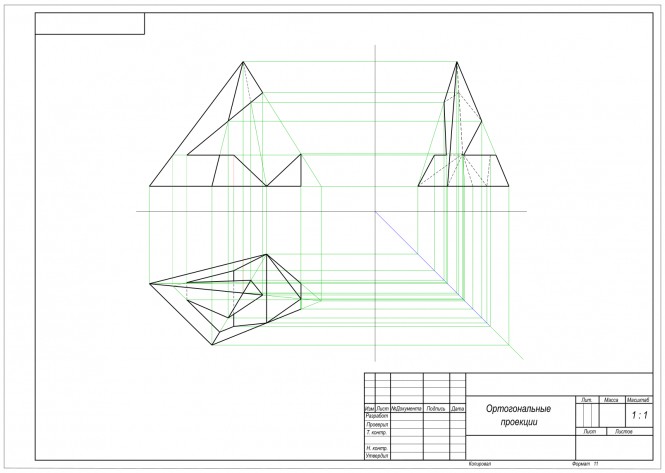
Построить точку N симметричную точке M относительно плоскости ABC КомментарииПостроить три проекции пирамиды с вырезом
Построить три проекции пирамиды с вырезом 
Построить три проекции пирамиды с вырезом Построение правильного пятиугольника с помощью циркуля : https://ingr.fxyz.ru/tasks/2011/ КомментарииМожете объяснить,а то когда я начинаю чертить по размером,у меня ничего не получается.Может окружность как то по другому чертить надо?
Построить горизонтальную проекцию замкнутой ломаной принадлежащей плоскости
Построить горизонтальную проекцию замкнутой ломаной принадлежащей плоскости 
Построить горизонтальную проекцию замкнутой ломаной принадлежащей плоскости КомментарииПровести горизонтально проецирующую плоскость α , перпендикулярную плоскости δ (ABC) и отстающую от точки E(E1, E2) на 20 мм.
Провести горизонтально проецирующую плоскость α , перпендикулярную плоскости δ (ABC) и отстающую от точки E(E1, E2) на 20 мм. Плоскость α задать следами.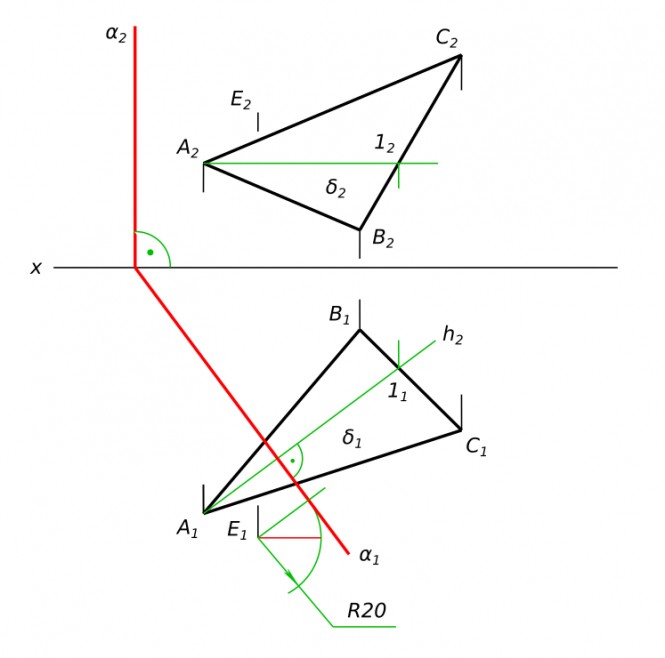 
Провести горизонтально проецирующую плоскость α , перпендикулярную плоскости δ (ABC) и отстающую от точки E(E1, E2) на 20 мм. Плоскость α задать следами. КомментарииЛежат ли точки в одной плоскости.
Лежат ли точки в одной плоскости? 
Лежат ли точки в одной плоскости? Если точки лежат в одной плоскости, то
$ D ⊂ ABC $ тогда
$ BD ∩ AC = 1 → B_{1}D_{1} ∩ A_{1}C_{1} = 1_{1} ^ B_{2}D_{2} ∩ A_{2}C_{2} = 1_{2} $ Но, на фронтльной проекции условие не выполняется. Из чего делаем вывод: точка D не принадлежит плоскости ABC. КомментарииПостроить недостающие проекции плоских фигур
Построить недостающие проекции плоских фигур КомментарииНайти недостающую проекцию точки A, принадлежащей плоскости
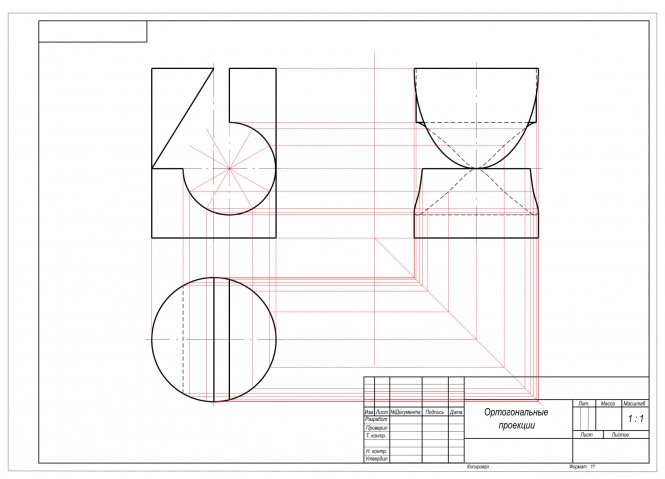
КомментарииПостроить в 3х проекциях геометрическое тело с вырезом
Построить в 3х проекциях геометрическое тело с вырезом 
Построить в 3х проекциях геометрическое тело с вырезом КомментарииПостроить линию пересечения плоскости Σ(h*f) и плоскости Q(a// b). Через т. К провести прямую // обеим плоскостям
Построить линию пересечения плоскости Σ(h*f) и плоскости Q(a// b). Через т. К провести прямую // обеим плоскостям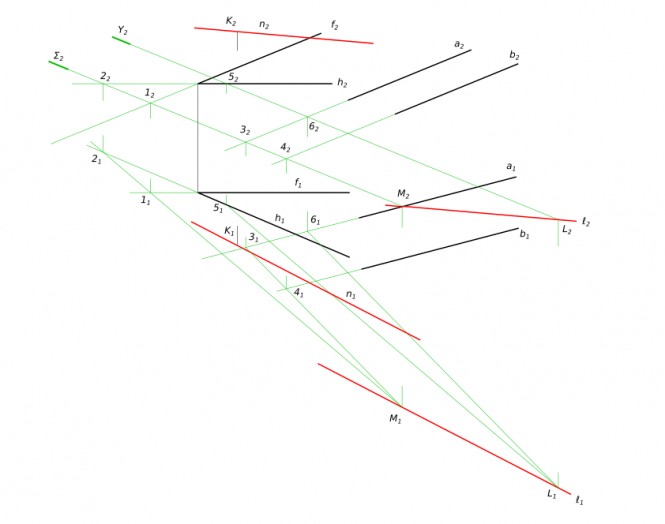 
Построить линию пересечения плоскости Σ(h*f) и плоскости Q(a// b). Через т. К провести прямую // обеим плоскостям КомментарииПостроить эпюр точки b,симметричной точке A(A1, A2) относительно оси y
Построить эпюр точки b,симметричной точке A(A1, A2) относительно оси y 
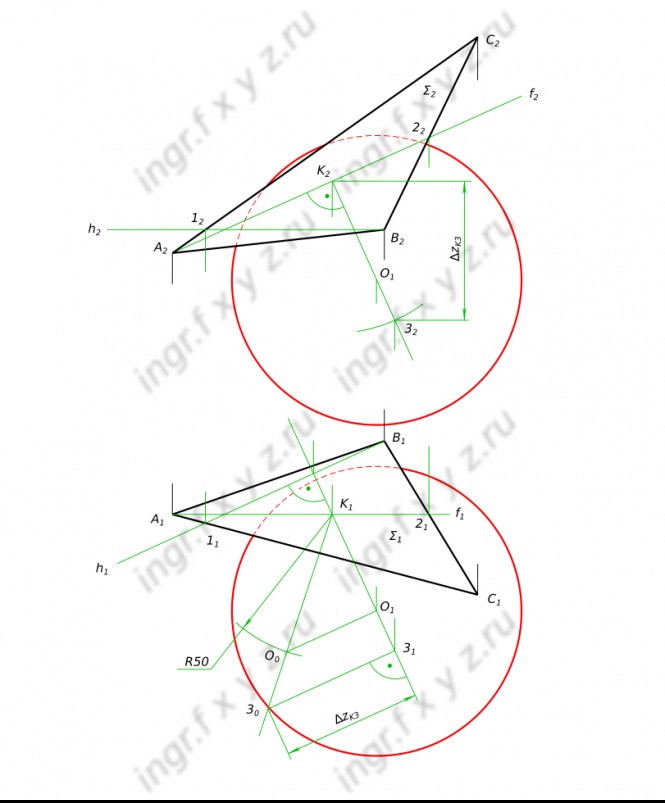
Построить эпюр точки b,симметричной точке A(A1, A2) относительно оси y КомментарииПостроить проекции шара радиусом 50 мм касающегося плоскости треугольника
Построить проекции шара радиусом 50 мм касающегося плоскости треугольника ABC, если дана фронтальная проекция центра шара 
Построить проекции шара радиусом 50 мм касающегося плоскости треугольника КомментарииПостроить равносторонний треугольник ABC с основанием BC равным 100 мм лежащим на прямой MN и вершиной A на прямой EF.
Построить равносторонний треугольник ABC с основанием BC равным 100 мм лежащим на прямой MN и вершиной A на прямой EF параллельной П2 и отстоящей от нее дальше чем прямая MN.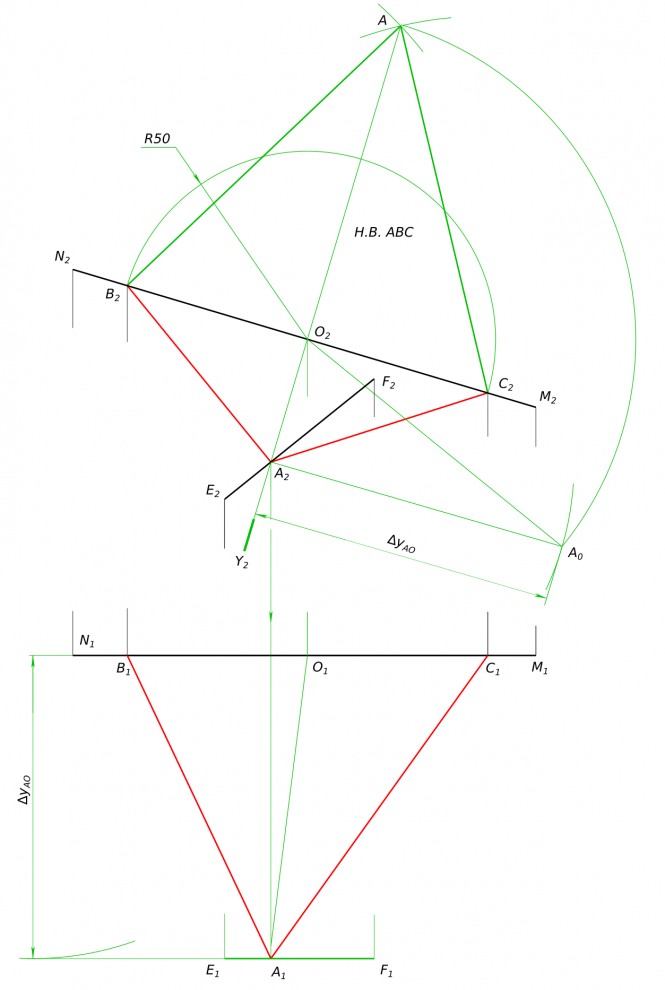 
Построить равносторонний треугольник ABC с основанием BC равным 100 мм лежащим на прямой MN и вершиной A на прямой EF. КомментарииПостроить три проекции пирамиды с вырезом
Построить три проекции пирамиды с вырезом 
Построить три проекции пирамиды с вырезом КомментарииЕсли возникнут вопросы по решенной задаче обращайтесь к https://ngeo.fxyz.ru
Подскажите, а как я могу посмотреть решенную задачу? У меня ничего кроме изображения с суммой не отображается
Попробуйте обновить страницу с открытой задачей. Для этого нажмите кнопку обновления (круг со стрелкой) . Это левее строки браузера. Или нажмите одновременно клавиши Ctrl F5.
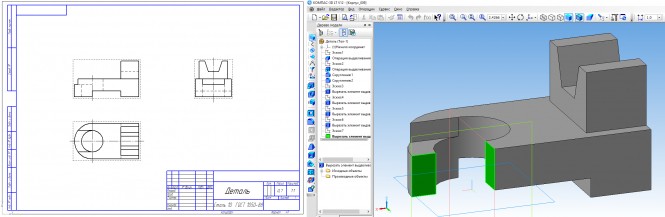
сделать разрез детали
Построить три вида детали и аксонометрию. Выполнить необходимые разрезы. 
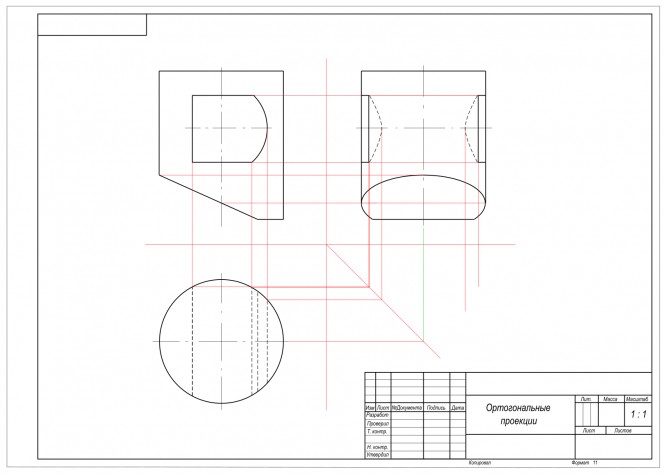
Построить три вида детали и аксонометрию. Выполнить необходимые разрезы. КомментарииПостроить три проекции цилиндра с вырезом
Построить три проекции цилиндра с вырезом 
Построить три проекции цилиндра с вырезом КомментарииМожете пожалуйста пронумеровать точки выреза
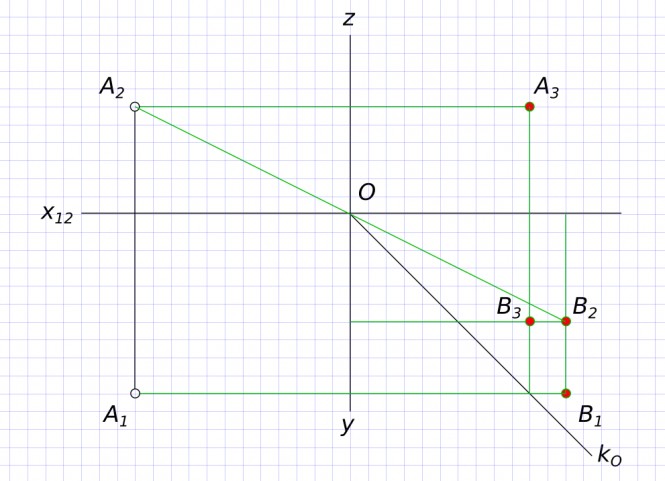
Построить проекции точек A,B,C, принадлежащих отрезкам, если
Построить проекции точек A,B,C, принадлежащих отрезкам, если
$ x_{A} = 50, z_{B} = 20, y_{C} = 25 $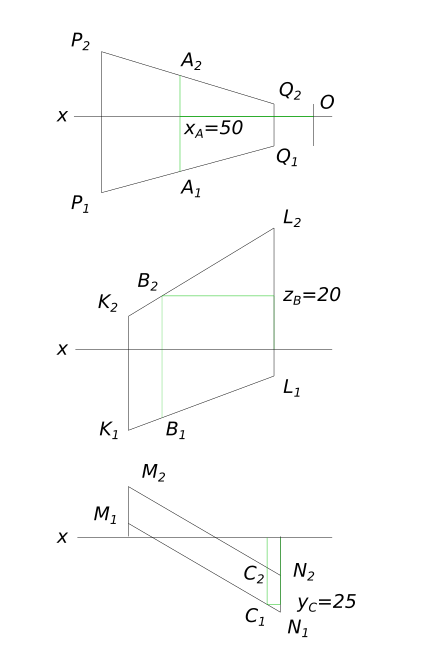 
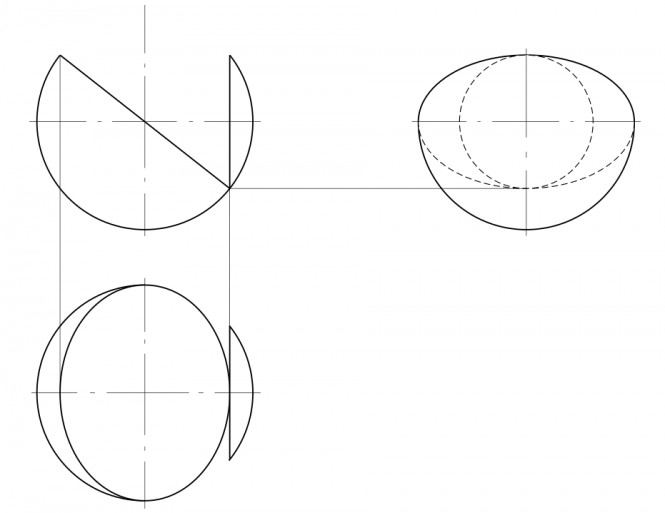
Построить проекции точек A,B,C, принадлежащих отрезкам, если КомментарииПостроить три проекции сферы с вырезом
Построить три проекции сферы с вырезом 
Построить три проекции сферы с вырезом КомментарииПостроить недостающую проекцию точки A, если она удалена от плоскости q(a//b) на расстоянии 20 мм
Построить недостающую проекцию точки A, если она удалена от плоскости q(a//b) на расстоянии 20 мм 
Построить недостающую проекцию точки A, если она удалена от плоскости q(a//b) на расстоянии 20 мм КомментарииЧерез точку A провести прямую l, пересекающую горизонталь
В плоскости сигма (m||n) построить горизонталь, фронталь и линию наибольшего ската. Через точку А провести прямую l, пересекающую горизонталь. Построить точку B над прямой l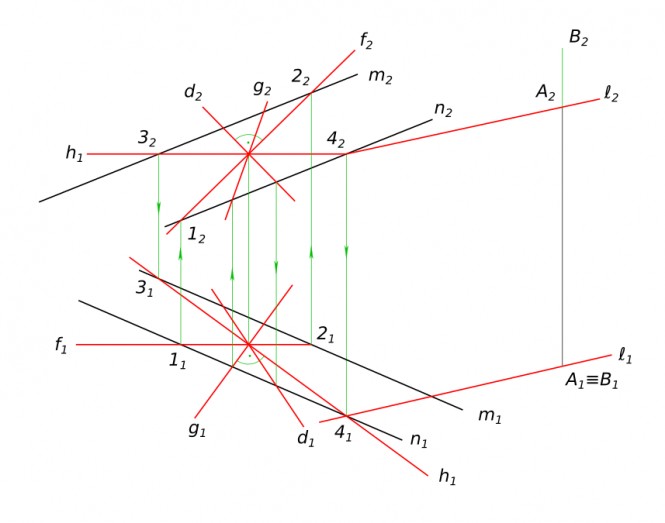 
В плоскости сигма (m||n) построить горизонталь, фронталь и линию наибольшего ската. Через точку А провести прямую l, пересекающую горизонталь. Построить точку B над прямой l КомментарииЧерез точку K провести прямую параллельную обеим плоскостям
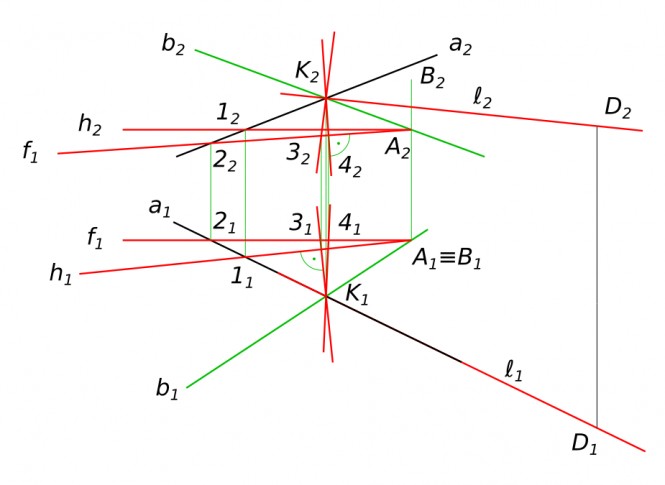
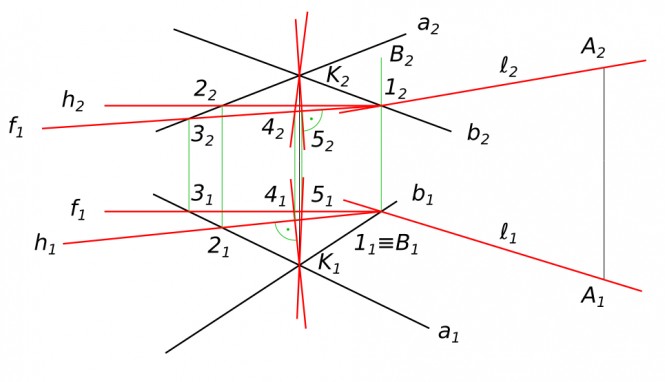
Построить линию пересечения плоскости Σ(a ∩ b) и плоскости Q (Q1). Через точку K провести прямую параллельную обеим плоскостям.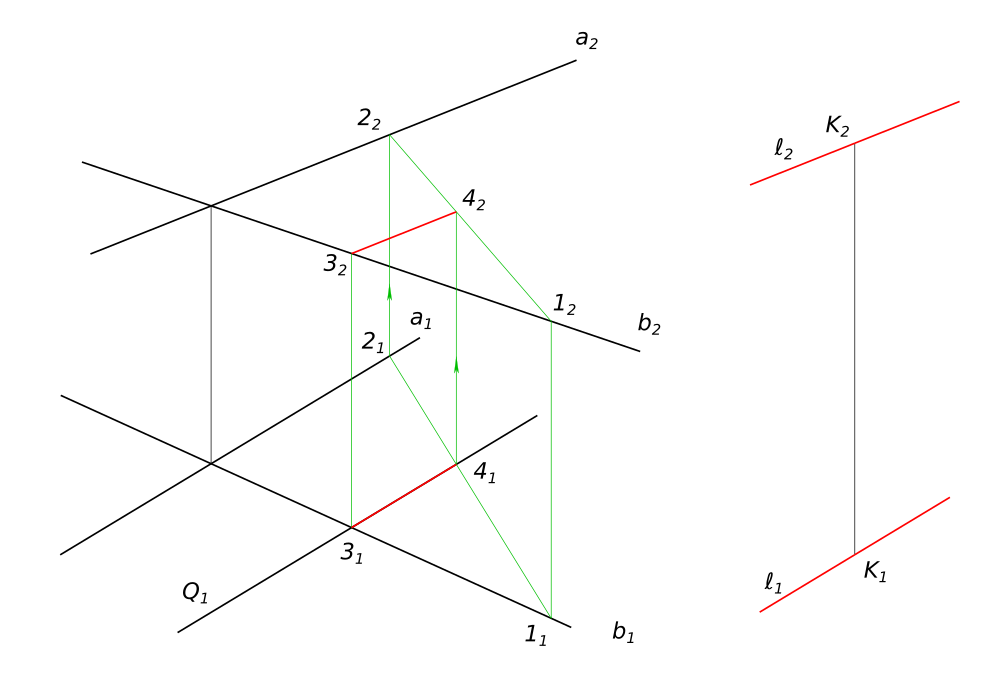 
Через точку K провести прямую параллельную обеим плоскостям Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи, получаем:
$ 1 - 2 ∈ Σ(a ∩ b) $
$ 3 - 4 = Σ ∩ Q$
$ ℓ ‖ 3 - 4 ⇔ ℓ_{1} ‖ 3_{1} - 4_{1}, ℓ_{2} ‖ 3_{2} - 4_{2} $ КомментарииПостроить точку пересечения прямой с плоскостью. Определить видимость.
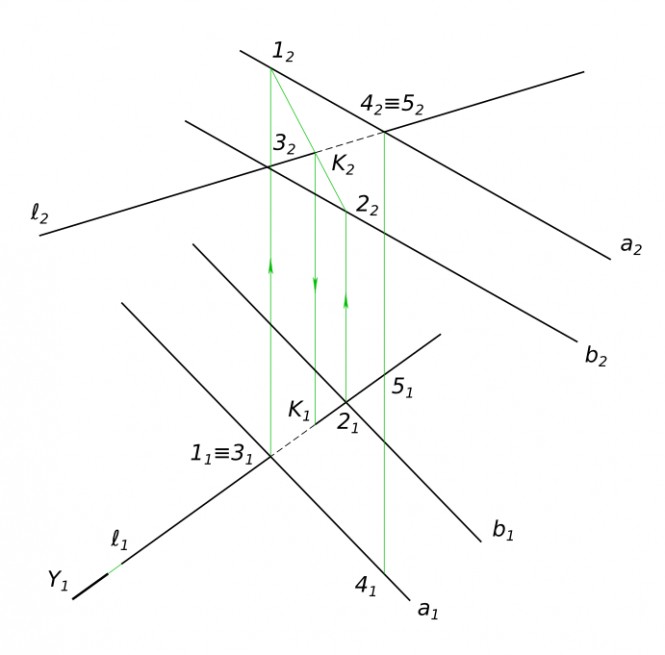
Построить точку пересечения прямой l с плоскостью Σ(a II b) и определить видимость прямой относительно плоскости Σ(a II b). 
Построение точки пересечения прямой с плоскостью Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи, получаем:
$ ℓ ⊂ Y $
$ 1 - 2 = Y ∩ Σ $
$ K = 1 - 2 ∩ ℓ $ Для определения видимости на горизонтальной плоскости проекций выбираем конкурирующие точки
$ 1 ∈ a, 3 ∈ ℓ $
$ 1 над 3 ⇒ прямая ℓ видима до точки встречи K $ Для определения видимости на фронтальной плоскости проекций выбираем конкурирующие точки
$ 4 ∈ a, 5 ∈ ℓ $
$ 4 перед 5 ⇒ прямая ℓ не видима до точки встречи K $ КомментарииПостроить три проекции пирамиды с вырезом
Построить три проекции пирамиды с вырезом 
Построение трех проекций пирамиды с вырезом КомментарииПостроить горизонталь, фронталь и линию наибольшего ската
Построить горизонталь, фронталь и линию наибольшего ската. Через точку D провести прямую, пересекающую прямую a. Построить точку B на плоскостью Σ(A: a). 
Построить горизонталь, фронталь и линию наибольшего ската КомментарииВ плоскости Σ(a*b) построить горизонталь, фронталь и линию наибольшего ската
В плоскости Σ(a∩b) построить горизонталь, фронталь и линию наибольшего ската. Через точку A провести прямую ℓ , пересекающую прямую b. Построить точку B над плоскостью Σ 
В плоскости Σ(a∩b) построить горизонталь, фронталь и линию наибольшего ската Комментарииподскажите, почему получается две линии наибольшего ската и b1 совпадает с 11, если нужно построить точку над плоскостью, а не на ней
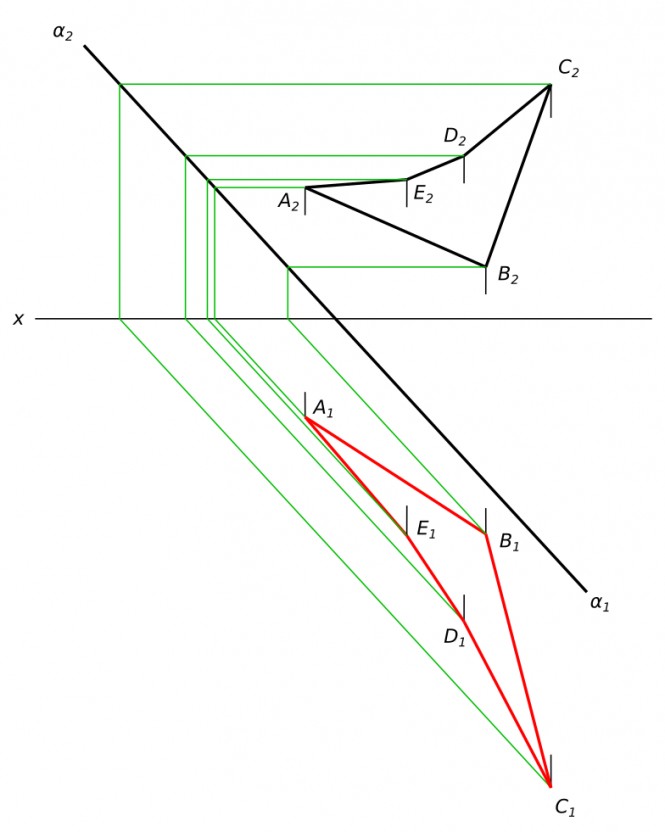
определить длину трубопровода
Данная задача относится к метрическим задачам(https://ngeo.fxyz.ru/метрические_задачи/)
$ L_{ABCDE} = |AB|+|BC|+|CD|+|DE| = A_{1}B_{1}+B_{1}C_{1}+C_{2}D_{2}+D_{1}E_{1} $ КомментарииПостроить три проекции пирамиды с вырезом
Построить три проекции пирамиды с вырезом 
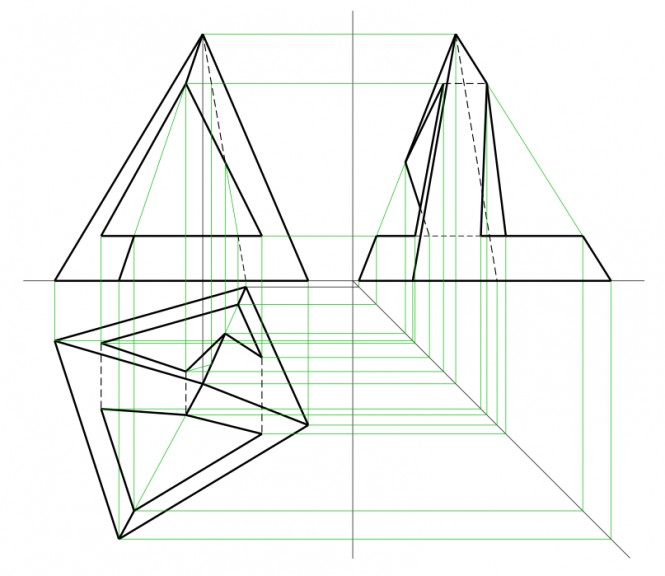
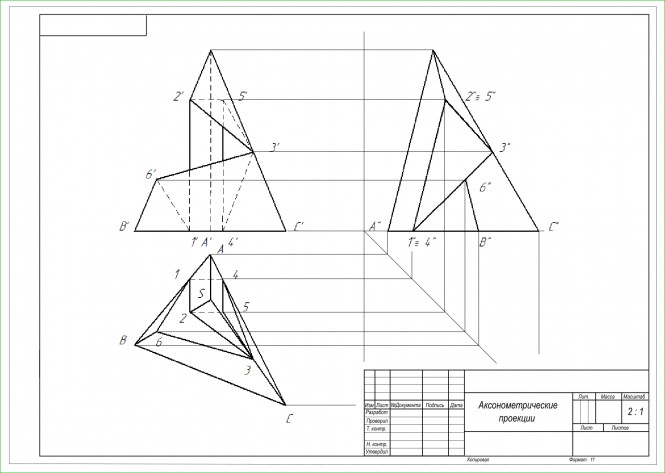
Построить три проекции пирамиды с вырезом Первоначально строим недостающую проекцию пирамиды. Призматический вырез составляют профильно проецирующие плоскости. В пересечении их между собой находятся прямые перпендикулярные профильной плоскости проекций Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи, получаем:
$ 1" ≡ 4" ⇔ 1' - 4' ‖ x, 1 - 4 ‖ x $
$ (1" - 2") ∈ (A"S"B") ⇔ (1' - 2') ∈ (A'S'B'), (1 - 2) ∈ (ASB) $
$ (1" - 2") ‖ A"S" ⇔ (1' - 2') ‖ A'S', (1 - 2) ‖ AS $
$ (4" - 5") ∈ (A"S"C") ⇔ (4' - 5') ∈ (A'S'C'), (4 - 5) ∈ (ASC) $
$ (4" - 5") ‖ A"S" ⇔ (4' - 5') ‖ A'S', (4 - 5) ‖ AS $ Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии