Все решения инженера @NICKПостроить эпюры поперечных сил Q и изгибающих моментов M, действующих в сечениях балки
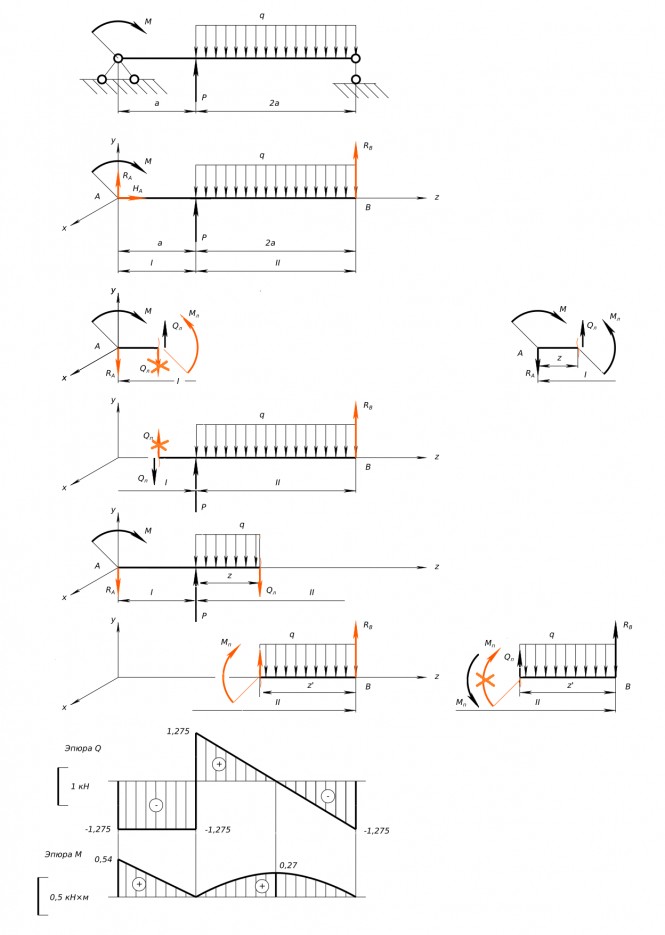
Построение эпюр поперечных сил Q и изгибающих моментов M, действующих в сечениях балки: 
Построение эпюр поперечных сил Q и изгибающих моментов M По предложенному в задании описанию вычерчиваем расчетную схему балки. Чтобы построить эпюры необходимо прежде всего определить реакции опор. Левую опору обозначим A, правую - B. В левой опоре возникают реакции: вертикальная RA и горизонтальная HA. В правой опоре только вертикальная - RB. Для нахождения значений опорных реакций составляем уравнения равновесия. Так как на балку не действуют горизонтальные силы, то HA=0. Момент силы принято считать положительным, если он вращает стержень против часовой стрелки и наоборот - если по часовой стрелке. Сумма моментов относительно опоры A:
$ ΣM_{A}=0=-M+Pa-q2a2a+R_{B}3a $ Учитывая, что M=qa^2, P=2qa получаем
$ R_{B}=\frac{3qa^{2}}{3a}=qa $ Сумма моментов относительно опоры B:
$ ΣM_{B}=0=-M-P2a+q2aa-R_{A}3a= $ Учитывая, что M=qa^2, P=2qa получаем
$ R_{A}=\frac{-3qa^{2}}{3a}=-qa $ RA найдена со знаком минус. Знак минус означает что направление RA противоположно принятому при составлении уравнения равновесия. Исправим это на расчетной схеме. Проверяем правильность определения опорных реакций, спроецировав все силы на вертикальную ось y:
$ ΣF_{y}=0=-R_{A}+P-q2a+R_{B}=-qa+2qa-2qa+qa $ Далее, разбиваем стержень на характерные участки. Границы участков проходят в местах расположения опор, а также точках приложения внешних сил или изменения закона их действия. Нагружение данной балки разбивается на два участка I и II. Поперечная сила, в каком-то сечении балки на каждом участке, равна сумме всех вертикальных сил действующих на балку по одну сторону от рассматриваемого сечения. Общепринято что: если слева от сечения рассматривается поперечная сила направленная вверх, то она положительна и наоборот если вниз; если справа от сечения рассматривается поперечная сила направленная вниз, то она положительна и наоборот если вверх. Возьмем произвольное сечение балки на участке I и найдем для него значение поперечной силы. Если рассматривать силы слева от сечения тогда:
$ Q_{л}=-R_{A}=-qa=3×0,425=-1,275 кН $ Если рассматривать силы справа от сечения тогда:
$ Q_{п}=-R_{B}+q2a-P=-qa-2qa+2qa=-qa=-1,275 кН $ Таким образом, значение поперечной силы не зависит от того с какой стороны от сечения рассматривать действующие силы. Построим эпюру поперечных сил на I участке балки. Так как значение поперечной силы не зависит ни от каких переменных, то ее эпюра будет представлять собой горизонтальную прямую, удаленную от нулевой линии на координату -1,275 кН. Возьмем произвольное сечение балки на участке II и найдем для него значение поперечной силы. Если рассматривать силы слева от сечения тогда:
$ Q_{л}=-R_{A}+P-qz=-qa+2qa-qz=qa-qz=q(a-z) $ Если рассматривать силы справа от сечения тогда:
$ Q_{п}=qz'- R_{B}=qz'-qa=q(z'-a) $ Как видно из уравнений, значение поперечной силы будет зависеть от координат z и z', характеризующих удаление сечения от концов участка. Поэтому, эпюра поперечной силы будет представлять собой наклонную прямую. Для ее построения необходимы две точки. Чтобы их получить рассмотрим сечения на концах участка. Когда сечение на левом конце участка
$ z=0; Q_{л}=q(a-0)=qa=3×0,425=1,275 кН $ Когда сечение на правом конце участка
$ z'=0; Qп=q(0-a)=-qa=-3×0,425=-1,275 кН $ На эпюре строим горизонтальную прямую для участка I и найденные для участка II точки Qл=1,275 кН, Qп=-1,275 кН и соединяем их прямой линией. Таким образом, эпюра поперечных сил по длине балки построена. Далее, действуя подобным образом, для построения эпюры изгибающих моментов M по длине балки. На каждом участке балки проводим произвольное сечение и составляем уравнение равновесия для левой или правой частей балки. Если нижние слои балки растянуты, то найденный момент положительный, если наоборот - отрицательный. Это правило знаков при нахождении изгибающих моментов в сечениях балки. Сечение на участке I. Рассматриваем силовые факторы слева от сечения.
$ M_{л}=M-R_{A}z=qa^{2}-qaz=qa(a-z) $ Где z - расстояние от точки приложения усилия до сечения I.
$ z=0; M_{л}=qa(a-0)=qa^{2}=3×0,425^{2}=0,54 кН×м $
$ z=a; M_{л}=qa(a-a)=0 $ Сечение на участке II. Рассматриваем силовые факторы справа от сечения.
$ M_{п}=R_{B}z'-qz'\frac{z'}{2}=qaz'-q\frac{z'^{2}}{2} $ В составленное уравнение равновесия входит переменная z' в квадрате, поэтому необходимы как минимум три точки для построения кривой.
$ z'=0; M_{п}=qa×0-q\frac{0^{2}}{2}=0 $
$ z'=a; M_{п}=qa^{2}-q\frac{a^{2}}{2}=q\frac{a^{2}}{2}=3\frac{0,425^{2}}{2}=0,27 кН×м $
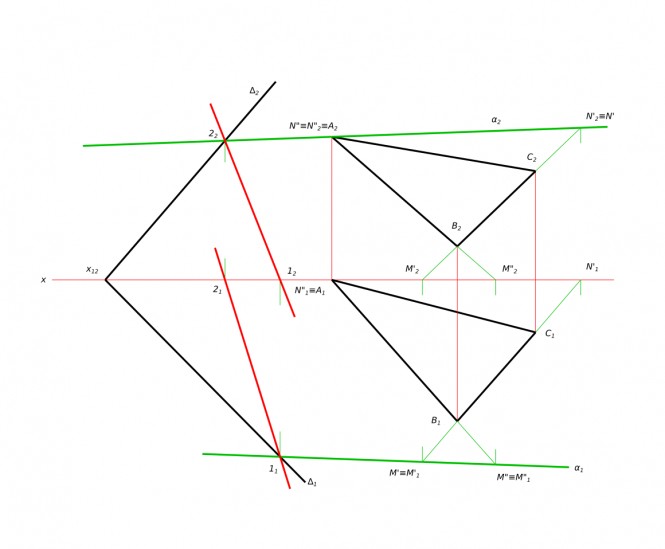
$ z'=2a; M_{п}=2qa^{2}-q\frac{4a^{2}}{2}=2qa^{2}-2qa^{2}=0 $ На эпюре строим точки найденные для участка I точки Mл=qa^2=0,54 кН×м, Mл=0 и наклонную прямую для участка I. И найденные для участка II точки Mп=0, Mп=qa^2/2=0,27 кН×м, Mп=0, соединяем их плавной кривой линией - параболой. Таким образом, эпюра изгибающих моментов по длине балки построена. Построить линию пересечения двух плоскостей
Построить линию пересечения плоскостей 
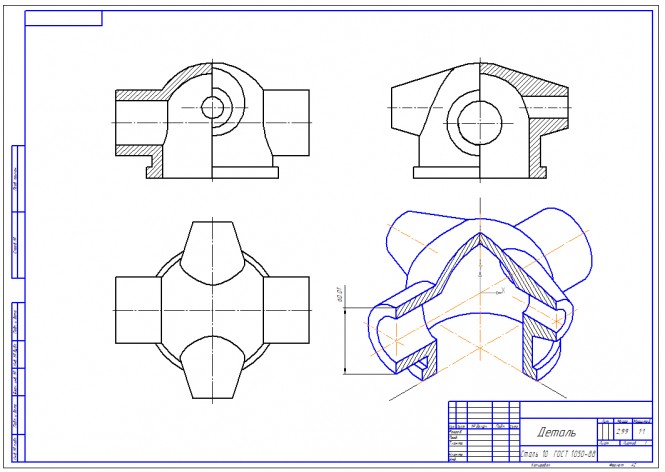
Построить линию пересечения плоскостей КомментарииПостроить третье изображение детали, дать разрезы, а также наглядное изображение детали в аксонометрической проекции.
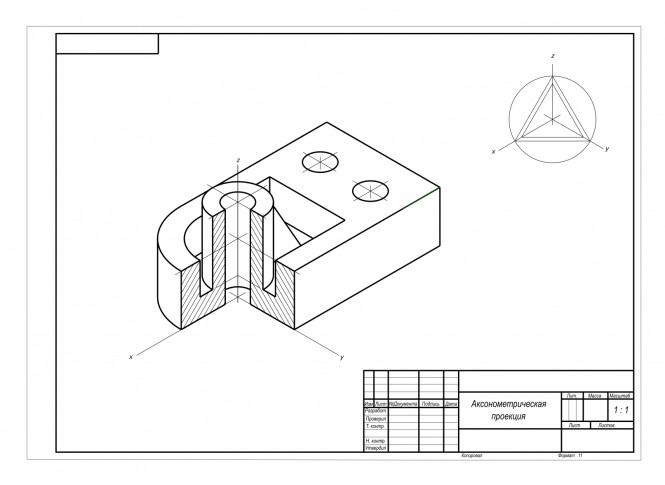
Наглядное изображение детали в аксонометрической проекции 
Наглядное изображение детали в аксонометрической проекции КомментарииПостроить третье изображение детали, дать разрезы, а также наглядное изображение детали в аксонометрической проекции.
Построить третье изображение детали, дать разрезы 
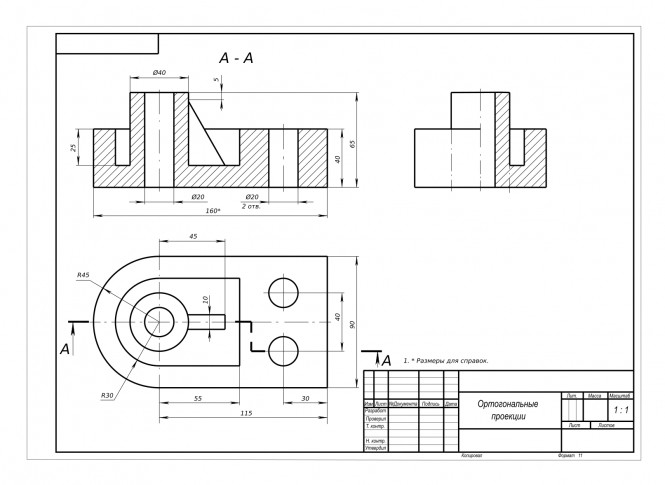
Построить третье изображение детали, дать разрезы КомментарииПостроить проекции и натуральный вид сечения тела плоскостью. Построить развертку усеченной части тела.
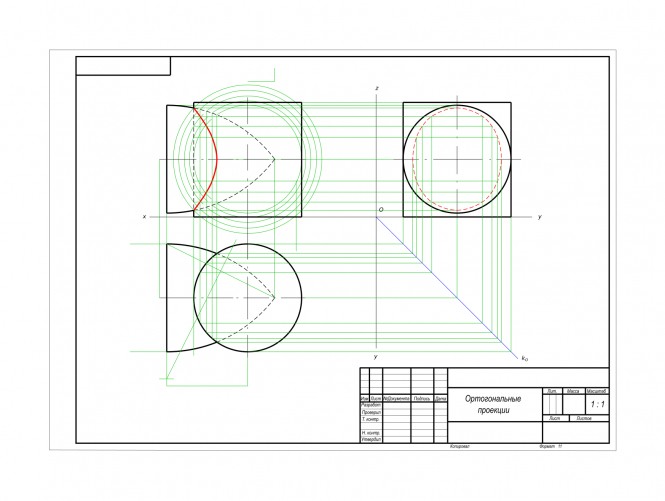
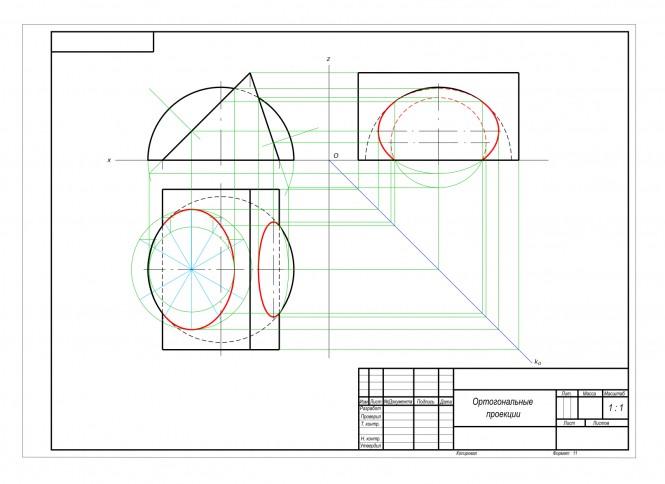
Построить проекции и натуральный вид сечения тела плоскостью. Построить развертку усеченной части тела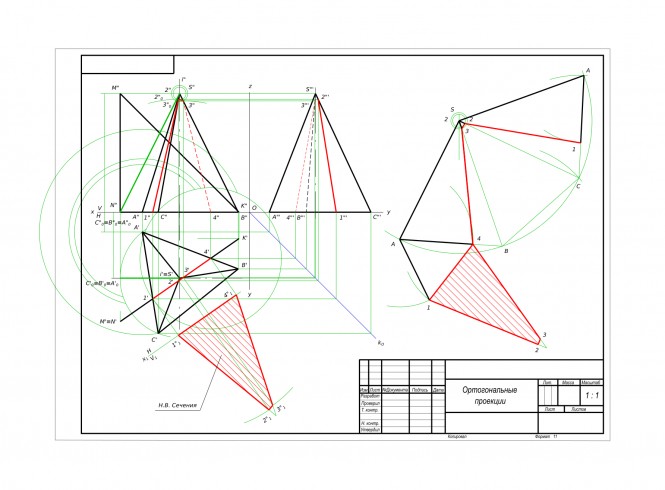 
Построить проекции и натуральный вид сечения тела плоскостью. Построить развертку усеченной части тела КомментарииПостроить проекции линий пересечения двух тел
Построить проекции линий пересечения двух тел 
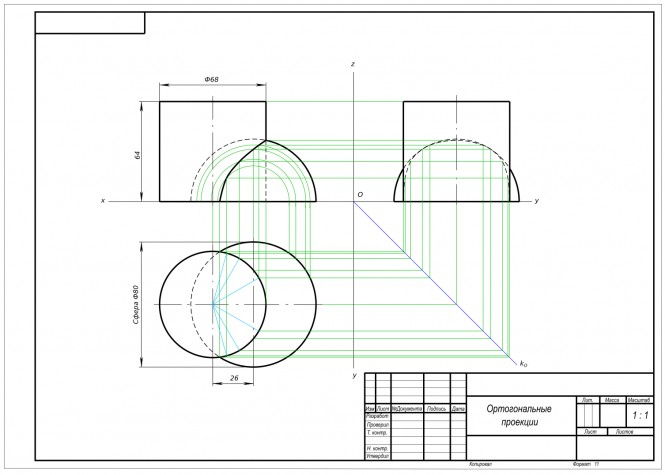
Построить проекции линий пересечения двух тел Проекции линии пересечения находим способом вспомогательных сфер. КомментарииПостроить проекции линий пересечения двух тел.
Построить проекции линий пересечения двух тел 
Построить проекции линий пересечения двух тел КомментарииПостроить проекции точки м, принадлежащей плоскости авс. Фронтальную проекцию точки м2 взять внутри треугольника произвольно.
Построить проекции точки м, принадлежащей плоскости авс. Фронтальную проекцию точки м2 взять внутри треугольника произвольно.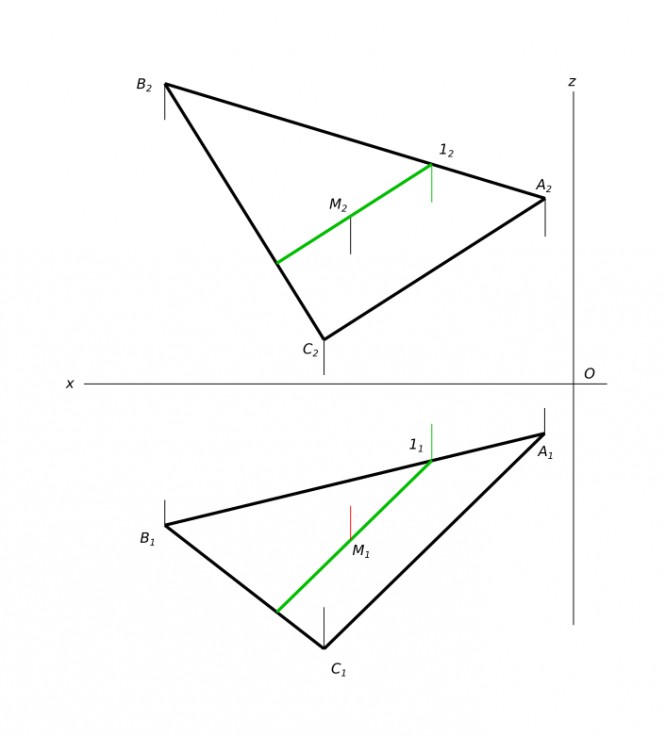 
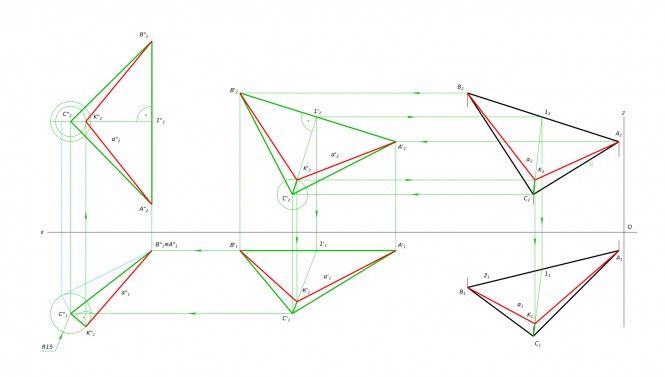
Построить проекции точки м, принадлежащей плоскости авс. Фронтальную проекцию точки м2 взять внутри треугольника произвольно. КомментарииПостроение точки пересечения прямой DF c плоскостью треугольника АВС, Подскажите правильно ли выполнено?
Построение точки пересечения прямой DF c плоскостью треугольника АВС КомментарииКак в КОМПАСе сделать чертеж и наглядное изображение?
Как в КОМПАСе сделать чертеж и наглядное изображение? Чтобы посмотреть решение вызовите контекстное меню кликнув правой кнопкой мыши на пиктограмме картинки и выберите «открыть изображение в новой вкладке». Как в КОМПАСе сделать чертеж и наглядное изображение? Предварительно в программе КОМПАС создается 3D модель и лишь затем в автоматическом режиме чертеж и наглядное изображение, которым требуется доработка в ручном режиме. См. https://ingr.fxyz.ru/tasks/2411/ Комментариипостроение третьего изображения по двум данным и линий перехода
Построение третьего изображения по двум данным и линий перехода 
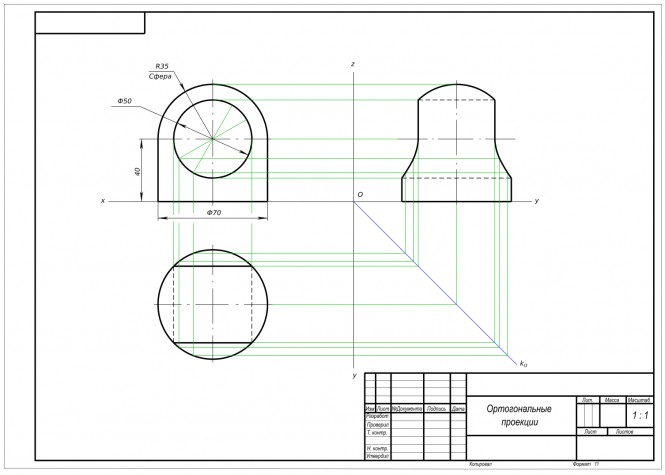
Построение третьего изображения по двум данным и линий перехода Комментарии43. Построить точки пересечения прямой a c полусферой
Построить точки пересечения прямой c полусферой 
Построить точки пересечения прямой c полусферой КомментарииЧерез прямую ав построить плоскость α удаленную от точки с на 15 мм
Через прямую ав построить плоскость α удаленную от точки с на 15 мм 
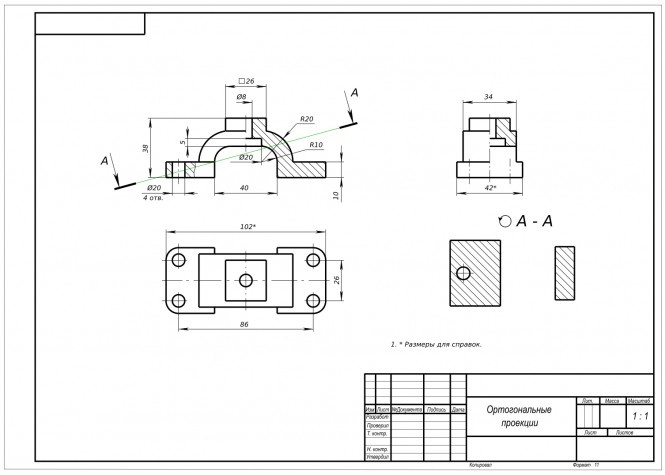
Через прямую ав построить плоскость α удаленную от точки с на 15 мм КомментарииПостроить три проекции детали, выполнить необходимые разрезы, построить наклонное сечение А-А
Построить три проекции детали, выполнить необходимые разрезы, построить наклонное сечение А-А 
Построить три проекции детали, выполнить необходимые разрезы, построить наклонное сечение А-А КомментарииЧерез точку e(60,?,45)провести отрезок |ef|=65 mm фронтальной прямой, пересекающей отрезок mn под прямым углом. m(40,0,10) ;n(1
Через точку e(60,?,45)провести отрезок\ef\=65mm фронтальной прямой, пересекающей отрезок mn под прямым углом. m(40,0,10) ;n(15,35,50).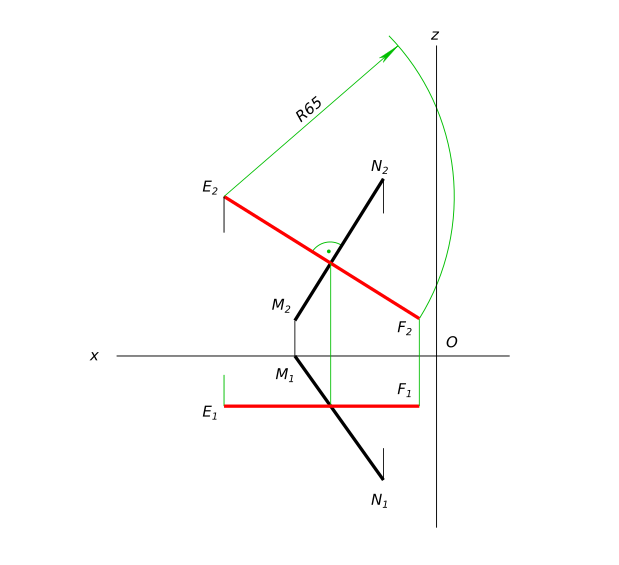 
Через точку e(60,?,45)провести отрезок\ef\=65mm фронтальной прямой, пересекающей отрезок mn под прямым углом. m(40,0,10) ;n(15,35,50). КомментарииПостроить три проекции геометрического тела с вырезом
Построить две проекции линии пересечения поверхностей 
Построить две проекции линии пересечения поверхностей КомментарииПостроить три проекции геометрического тела с вырезом
Построить три проекции геометрического тела с вырезом 
Построить три проекции геометрического тела с вырезом КомментарииПостроить плоскость параллельную заданной двумя пересекающимися прямыми b и d так, чтобы отрезок прямой ℓ, заключенный между пл
Построить плоскость параллельную заданной двумя пересекающимися прямыми b и d так, чтобы отрезок прямой ℓ, заключенный между плоскостями, имел длину 40 мм. 
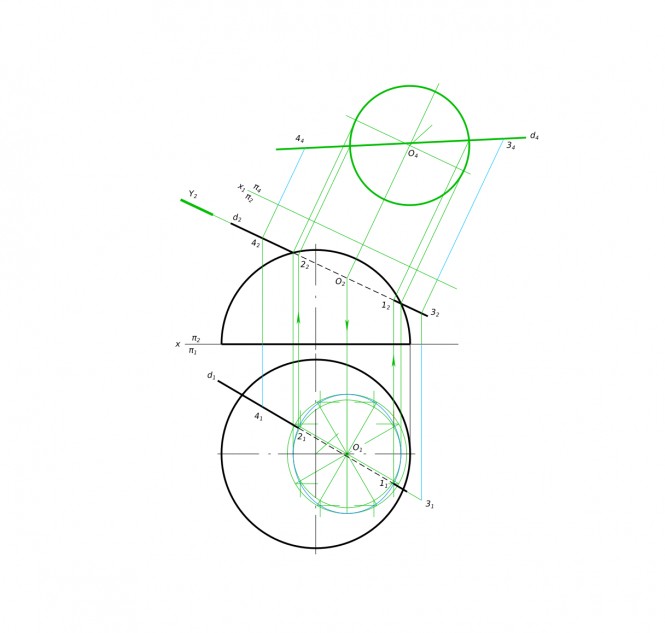
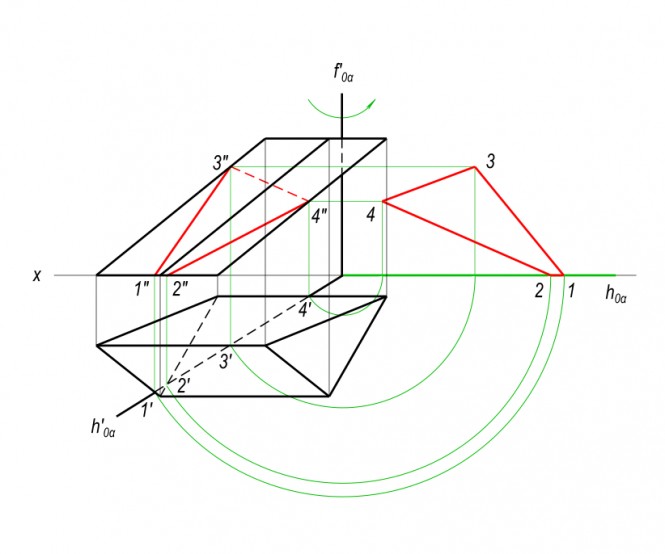
Построить плоскость параллельную заданной двумя пересекающимися прямыми b и d так, чтобы отрезок прямой ℓ, заключенный между плоскостями, имел длину 40 мм. КомментарииПостроить линию пересечения поверхности проецирующей плоскостью. Найти истинную величину сечения
Построить линию пересечения поверхности проецирующей плоскостью. Найти истинную величину сечения 
Построить линию пересечения поверхности проецирующей плоскостью. Найти истинную величину сечения КомментарииПостроить равносторонний треугольник если его основание - отрезок ab //п1, а направление высоты происходит через ось проекции x
Построить равносторонний треугольник если его основание - отрезок ab //п1, а направление высоты происходит через ось проекции x12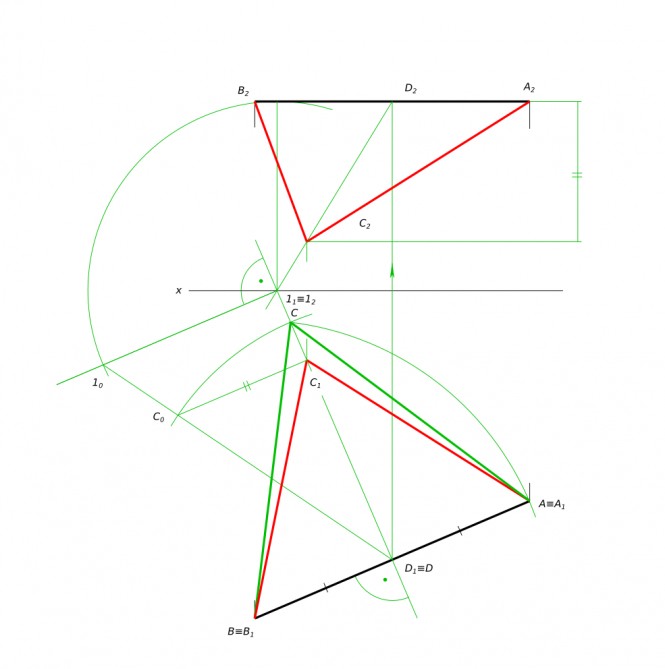 
Построить равносторонний треугольник если его основание - отрезок ab //п1, а направление высоты происходит через ось проекции x12 КомментарииЧерез точку A провести прямую l, пересекающую прямые q и a
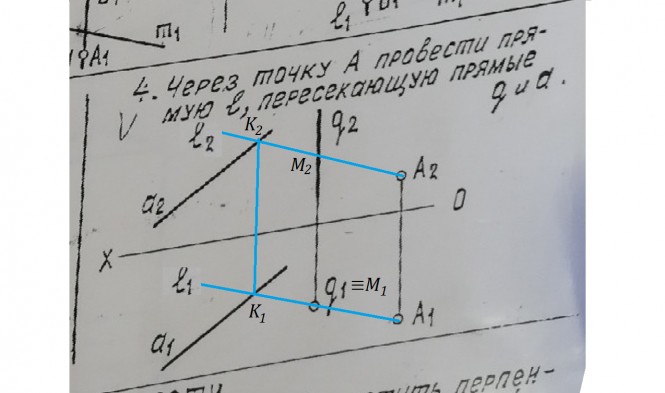
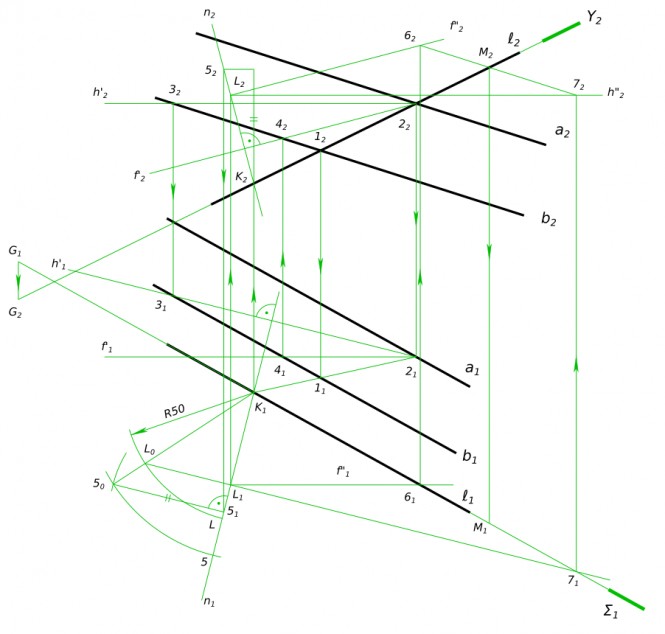
Через точку A провести прямую l, пересекающую прямые q и a
$ ℓ_{1} ≡ q_{1} ∧ ℓ_{1} ≡ A_{1} $
$ ℓ ∩ a = K ⇔ ℓ_{1} ∩ a_{1}=K_{1} ∧ ℓ_{2} ∩ a_{2}=K_{2} $
$ ℓ ∩ q ⇔ ℓ_{1} ∩ q_{1}=M_{1} ∧ ℓ_{2} ∩ q_{2}=M_{2} $ 
Через точку A провести прямую l, пересекающую прямые q и a КомментарииЗадача 3. Достроить вид сверху и построить вид слева с разрезом. Задача 5. Достроить вид сверху и построить вид слева конуса с вырезом.
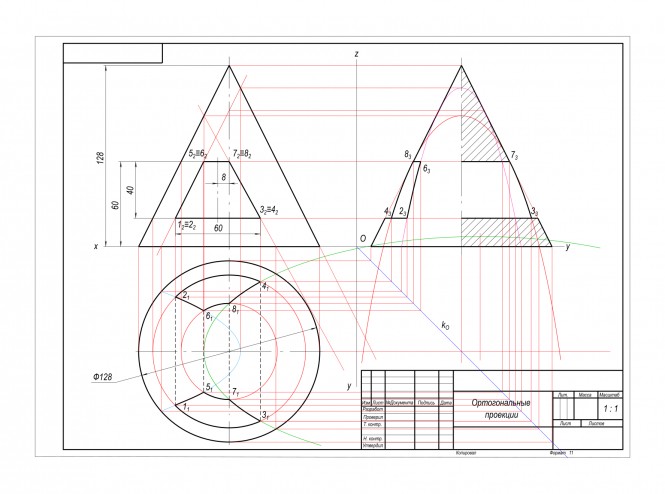
Задача 5. Достроить вид сверху и построить вид слева конуса с вырезом 
Задача 3. Выполнить задания, линии построения сохранить, нанести размеры, масштаб натуральный. Задача 3. Достроить вид сверху и построить вид слева с разрезом. Задача 5. Достроить вид сверху и построить вид слева конуса с вырезом.
Задача 3. Достроить вид сверху и построить вид слева с разрезом пирамиды с вырезом 
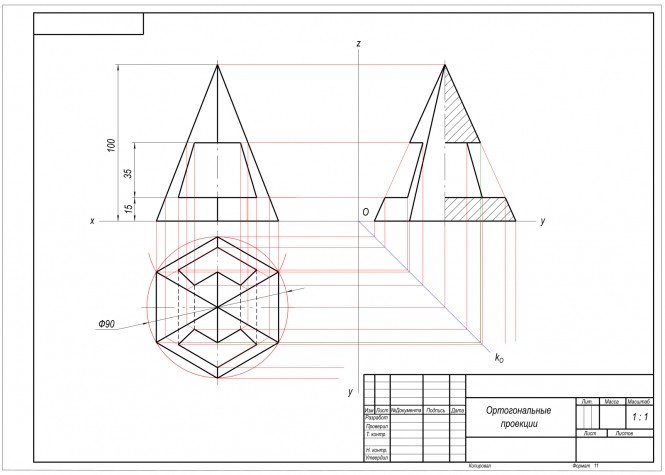
Задача 3. Достроить вид сверху и построить вид слева с разрезом пирамиды с вырезом Построить проекции точки K принадлежащей плоскости α(abc) и равноудаленной от трех плоскостей проекций
Построить проекции точки K принадлежащей плоскости α(abc) и равноудаленной от трех плоскостей проекций 
Построить проекции точки K принадлежащей плоскости α(abc) и равноудаленной от трех плоскостей проекций КомментарииНа плоскости α(авс) построить множество точек, равноудаленных от плоскостей проекций p1 и p2. Координаты точек: а(10,5,25), в(4
На плоскости α(авс) построить множество точек, равноудаленных от плоскостей проекций p1 и p2. Координаты точек: а(10,5,25), в(45,45,10), с(65,30,50).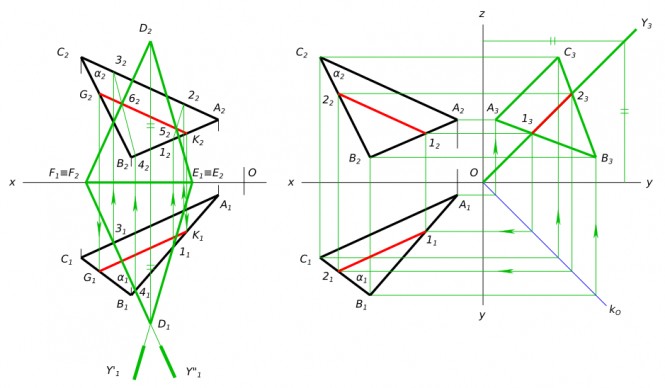 
На плоскости α(авс) построить множество точек, равноудаленных от плоскостей проекций p1 и p2. Координаты точек: а(10,5,25), в(45,45,10), с(65,30,50). КомментарииНайти на прямой ℓ проекции точек, отстоящих от плоскости a//b на расстоянии 50 мм
Найти на прямой ℓ проекции точек, отстоящих от плоскости a//b на расстоянии 50 мм 
Найти на прямой ℓ проекции точек, отстоящих от плоскости a//b на расстоянии 50 мм КомментарииСпроектировать привод цепного конвейера.
Спроектировать привод цепного конвейера 
Спроектировать привод цепного конвейера КомментарииЗаданы координаты точки A. Построить ее аксонометрические и ортогональные проекции а также: - точки B симметричной точке A
Задача 1. Заданы координаты точки A. Построить ее аксонометрические и ортогональные проекции, а также точек: - точки B симметричной точке A относительно горизонтальной плоскости проекций; - точки C, симметричной точке A относительно фронтальной плоскости проекций; - точки D симметричной точке A относительно оси проекций; - точки K симметричной точке A относительно плоскости симметрии. Координаты всех точек указать в таблице на эпюре.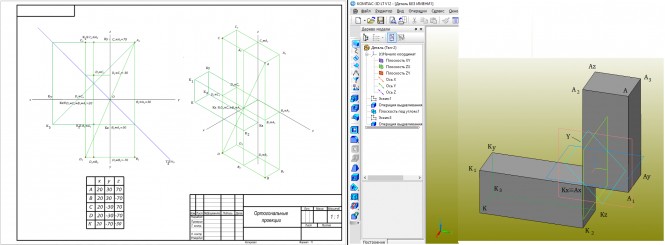 
Задача 1. Заданы координаты точки A. Построить ее аксонометрические и ортогональные проекции, а также точек: - точки B симметричной точке A относительно горизонтальной плоскости проекций; - точки C, симметричной точке A относительно фронтальной плоскости проекций; - точки D симметричной точке A относительно оси проекций; - точки K симметричной точке A относительно плоскости симметрии КомментарииНа прямой, проходящей через точки a и b, построить точку c, удаленную от п1 на 20 мм, точку d, удаленную от п2 на 15 мм, точку
На прямой, проходящей через точки a и b, построить точку c, удаленную от п1 на 20 мм, точку d, удаленную от п2 на 15 мм, точку m ∈ п1, точку n ∈ п2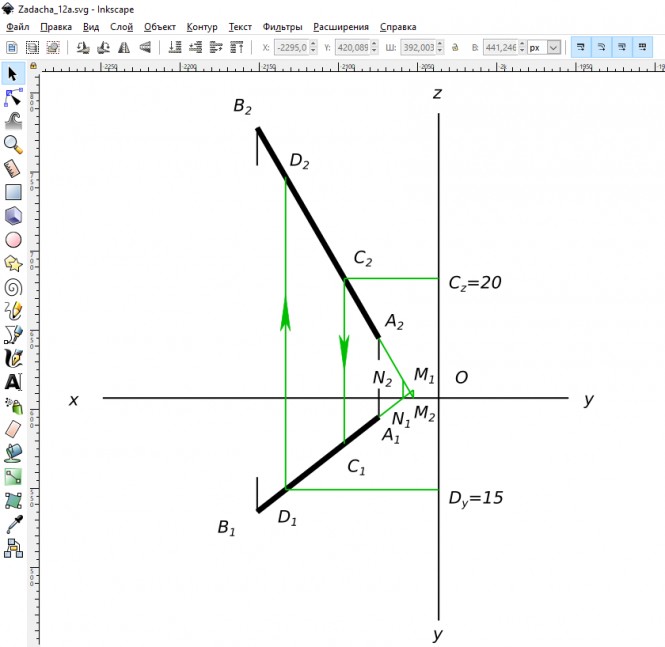 
На прямой, проходящей через точки a и b, построить точку c, удаленную от п1 на 20 мм, точку d, удаленную от п2 на 15 мм, точку m ∈ п1, точку n ∈ п2 КомментарииЧерез точку a провести отрезок фронтали длиной 40 мм, восходящий влево под углом 60° к плоскости П1. а (10; 15; 10)
Через точку a провести отрезок фронтали длиной 40 мм, восходящий влево под углом 60° к плоскости П1: а (10; 15; 10); 2) a (20; –15; –40)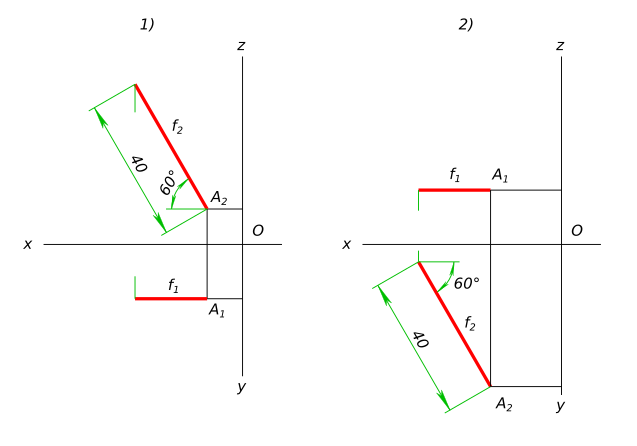 
Через точку a провести отрезок фронтали длиной 40 мм, восходящий влево под углом 60° к плоскости П1: а (10; 15; 10); 2) a (20; –15; –40) Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии