Все решения инженера @NICKРасчет подшипников качения на заданный ресурс
2. Радиальные реакции опор от действия муфты. Радиальная жесткость муфты МУВП
$ C_{p} = 610 T_{H}^{0,333} = 610 × 51,4^{0,333} = 2267,74 Н/мм $ Радиальная сила Fк на валу от упругой муфты
$ F_{к} = C_{p} ∆ = 2267,74 × 0,3 = 680,32 Н $ Реакции от силы Fк Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{к}(ℓ +ℓ_{2}) — R_{2к}ℓ = 0; $
$ R_{2к}= \frac{F_{к}(ℓ +ℓ_{2})}{ℓ}=\frac{680,32(192+80)}{192} = 963,79 Н; $
$ ΣM_{2}=0; F_{к}ℓ_{2} — R_{1к}ℓ = 0; $
$ R_{1к}= \frac{F_{к}ℓ_{2}}{ℓ}= \frac{680,32×80}{192} = 283,47 Н; $ Проверка:
$ — F_{к} +R_{2к}-R_{1к}= — 680,32 + 963,79 — 283,47 = 0; $ Реакции найдены правильно. 3. Реакции опор для расчета подшипников:
$ F_{r1max} = R_{1} + R_{1к} = 1042,38 + 283,47 = 1325,85 Н; $
$ F_{r2max} = R_{2} + R_{2к} = 1042,38 + 963,79 = 2006,17 Н; $ Внешняя осевая сила действующая на вал,
$ F_{Amax} = F_{a} = 0 Н $ 4. Для типового режима нагружения III коэффициент эквивалентности
$ K_{E} = 0,56 $ Вычисляем эквивалентные нагрузки:
$ F_{r1} = K_{E}F_{r1max} = 0,56 ∙ 1325,85 = 742 Н; $
$ F_{r2} = K_{E}F_{r2max} = 0,56 ∙ 2006,17 = 1123 Н; $
$ F_{A} = K_{E}F_{Amax} = 0,56 × 0 = 0 Н. $ 5. Предварительно назначаем шариковые радиальные подшипники серии диаметров 2: 207. Схема установки подшипников - враспор. 6. Для принятых подшипников из табл. 24.10 [1] находим: Cr = 25500 Н; C0r = 13700 Н; d=35 мм; D=72 мм; Dω=11,112 мм; α = 0°. 7. При установке вала на двух радиальных шариковых подшипниках осевая сила Fa, нагружающая подшипник, равна внешней осевой силе, действующей на вал. Fa = FA Для радиальных шарикоподшипников из условия равновесия вала следует: Fa1 = 0; Fa2 = FA = 0. Дальнейший расчет производим для более нагруженного подшипника опоры 2. 8. Отношение Dωcosα/Dpω = 11,112∙1/53,5 = 0,2077, где Dpω =0,5(D+d)=0,5(72+35)=53,5 мм. В соответствии с табл. 7.3 имеем f0=13,7 Коэффициент осевого нагружения (см. табл. 7.2) e=0,28(f0Fa/C0r)0,23=0,28(13,7×0/13700)0,23=0 9. Отношение Fa/(VFr)=0/(1×1123)=0, что больше e=0 (V=1 при вращении внутреннего кольца). Окончательно принимаем (см. табл. 7.2): X=0,56; Y=0,44/e 10. Принимаем Kб =1,4 [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o). Эквивалентная динамическая радиальная нагрузка
$ P_{r} = (VXF_{r} + YF_{a})K_{б}K_{т}= $
$ = (1 × 0,56 × 1123 + Y × 0) × 1,4 × 1 = 880 Н $ 11. Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
$ L10ah = a_{1}a_{23}(\frac{C_{r}}{P_{r}})k(\frac{10^{6}}{60n}) = $
$ = 1 × 0,7 × (\frac{25500}{880} )^{3}×(\frac{10^{6}}{60×1445}) = 196450 ч. $ 6. Так как расчетный ресурс больше требуемого: L10ah > L'10ah (196450 > 33533,28), то предварительно назначенный подшипник 207 пригоден. При требуемом ресурсе 90%. Расчет подшипников качения на заданный ресурс
Расчет подшипников качения на заданный ресурс. Входной вал. 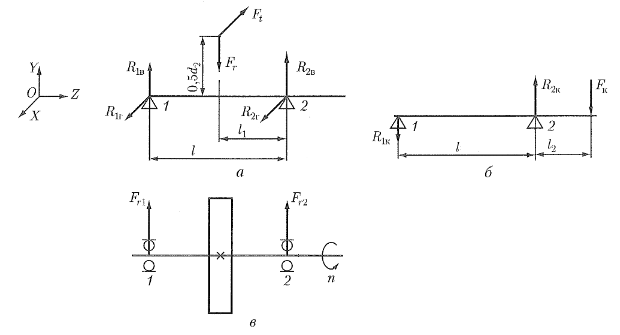
Расчет подшипников качения на заданный ресурс Линейные размеры: ℓ=192 мм; ℓ1=96 мм; ℓ2=80 мм; d1=52,5 мм. 1. Радиальные реакции опор от сил в зацеплении: в плоскости YOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{r}(ℓ-ℓ_{1}) + \frac{F_{a}d_{1}}{2} – R_{2в}ℓ=0; $
$ R_{2в}=\frac{F_{r}(ℓ-ℓ_{1})+\frac{F_{a}d_{1}}{2}}{ℓ}= $
$ = \frac{713,1(192-96)+0}{192}=356,55 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2}=0; R_{1в}ℓ + \frac{F_{a}d_{1}}{2} – F_{r}ℓ_{1}=0; $
$ R_{1в}=\frac{F_{r}ℓ_{1}- \frac{F_{a}d_{1}}{2}}{ℓ}= $
$ = \frac{713,1×96-0}{192}=356,55 Н; $ Проверка: Сумма проекций всех сил на ось Y равны нулю
$ ΣY=R_{1в} – F_{r} + R_{2в}=356,55 – 713,1 + 356,55 = 0; $ Значит реакции найдены правильно. в плоскости XOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; R_{2г}ℓ — F_{t}(ℓ-ℓ_{1})=0; $
$ R_{2г} = \frac{F_{t}(ℓ-ℓ_{1})}{ℓ}= \frac{1959(192-96)}{192}=979,5 Н; $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2}=0; - R_{1г}ℓ + F_{t}ℓ_{1} = 0; $
$ R_{1г} = \frac{F_{t}ℓ_{1}}{ℓ} =\frac{1959×96}{192} = 979,5 Н; $ Проверка: Сумма проекций всех сил на ось X равны нулю
$ ΣX= R_{1г} – F_{t} +R_{2г} = 979,5 -1959 +979,5 = 0; $ Реакции найдены правильно. Суммарные реакции опор:
$ R_{1} = (R_{1г}^{2}+ R_{1в}^{2})^{0,5} = $
$ (979,5^{2} + 356,55^{2})^{0,5} = 1042,38 Н; $
$ R_{2} = (R_{2г}^{2}+ R_{2в}^{2})^{0,5} = $
$ (979,5^{2} + 356,55^{2})^{0,5} = 1042,38 Н; $ КомментарииКонструирование зубчатых колес
Спроектировать привод цепного конвейера Конструирование зубчатых колес Первая ступень По результатам разработки эскизного проекта были вычерчены контуры зубчатых колес и червяков. Следующим шагом является конструктивная обработка их формы. [1, стр. 62] Шестерня Форма зубчатого колеса может быть плоской (рис. а, б) или с выступающей ступицей (рис. в). Значительно реже (в одноступенчатых редукторах) колеса делают со ступицей, выступающей в обе стороны.[1, стр. 62] 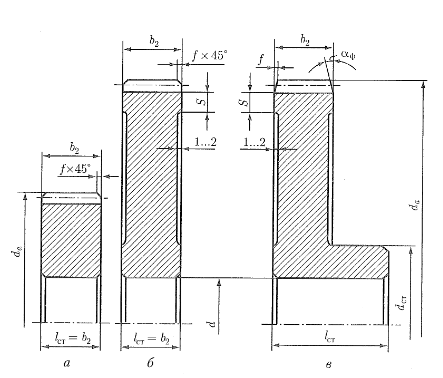
Конструирование зубчатых колес На рисунке показаны простейшие формы колес, изготовляемых в единичном и мелкосерийном производстве. Чтобы уменьшить объем точной обработки резанием, на дисках колес выполняют выточки (рис., б, в). При диаметре da < 80 мм эти выточки, как правило, не делают (рис. 13, а). [1, стр. 62] Так как da1 < 80 , то выточки не производим
$ d_{a_{1}} = 60,59 мм $ Длину ℓст посадочного отверстия колеса желательно принимать равной или больше b2 зубчатого венца (ℓст>b2). Принятую длину ступицы согласуют с расчетной (см. расчет соединения шлицевого, с натягом или шпоночного, выбранного для передачи вращающего момента с колеса на вал) и с диаметром посадочного отверстия d [1, стр. 63]: ℓст = (0,8...1,5)d, обычно ℓст = (1,0...1,2)d. Так как зубчатое колесо выполнено совместно с валом, то рассчитывать ступицу нет необходимости. На торцах зубчатого венца (зубьях и углах обода) выполняют фаски f = (0,5...0,6)m, которые округляют до стандартного значения (см. ниже). [1, стр. 63] На прямозубых зубчатых колесах при твердости рабочих поверхностей менее 350 HB - под углом αф = 45o (рис. 13, а, б), а при более высокой твердости αф = 15...20o(рис. 13, в). [1, стр. 63] Фаска венца
$ f = 0,5m = 0,5 × 1,75 = 0,88 мм $ округленная до стандартного значения
$ f = 1 мм $ Зубчатое колесо Так как 272,5 = da2 > 80 , то выточки выполним на торце колеса глубиной 2 мм. Длина ступицы колеса
$ ℓ_{ст} = 1,2d = 1,2 × 54 = 64,8 мм $ Ширину S торцов зубчатого венца принимают [1, стр. 63]:
$ S = 2,2m + 0,05b2 = 2,2 × 1,75 + 0,05 × 50 = 6,4 мм $ где m - модуль зацепления, мм. Фаска венца
$ f = 0,5m = 0,5 × 1,75 = 0,88 мм $ Конструирование зубчатых колес Вторая ступень По результатам разработки эскизного проекта были вычерчены контуры зубчатых колес и червяков. Следующим шагом является конструктивная обработка их формы. [1, стр. 62] Шестерня
$ d_{a_{1}} = 113,34 мм $ Так как da1 > 80 , то выточки выполним на торце колеса глубиной 2 мм. Длину ℓст посадочного отверстия колеса желательно принимать равной или больше b2 зубчатого венца (ℓст>b2). Принятую длину ступицы согласуют с расчетной (см. расчет соединения шлицевого, с натягом или шпоночного, выбранного для передачи вращающего момента с колеса на вал) и с диаметром посадочного отверстия d [1, стр. 63]: ℓст = (0,8...1,5)d, обычно ℓст = (1,0...1,2)d Принимаем
$ ℓ_{ст} = 1,2 × 45 = 54 мм $ Ширину S торцов зубчатого венца принимают [1, стр. 63]:
$ S = 2,2m + 0,05b2 = 2,2 × 2,0 + 0,05 × 50 = 6 мм $ Фаска венца
$ f = 0,5m = 0,5 × 2,75 = 1,38 мм $ округленная до стандартного значения
$ f = 1,6 мм $ Зубчатое колесо
$ d_{a_{2}} = 322,66 мм $ Принимаем
$ ℓ_{ст} = 1,2d = 1,2 × 72,5 = 87 мм $ При ℓст>b2 выступающую часть ступицы располагают по направлению действия осевой силы Fa в зацеплении. [1, стр. 63] Диаметр dст назначают в зависимости от материала ступицы: для стали dст = (1,5...1,55)d; чугуна dст = (1,55...1,6)d; легких сплавов dст = (1,6...1,7)d: меньшие значения для шлицевого колеса с валом, большие - для шпоночного и соединения с натягом. [1, стр. 63]
$ d_{ст} = 1,55d = 1,55 × 72,5 = 112,375 мм $ Назначаем
$ ℓ_{ст} = 45 мм; d_{ст} = 112 мм $
$ S = 2,2m + 0,05b2 = 2,2 × 2,0 + 0,05 × 32 = 6 мм $ Фаска венца
$ f = 0,5m = 0,5 × 2,75 = 1,38 мм; f = 1,6 мм $ Ширину S торцов зубчатого венца принимают [1, стр. 63]: Округлим полученные значения до целых Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил. КомментарииНачертить три вида детали
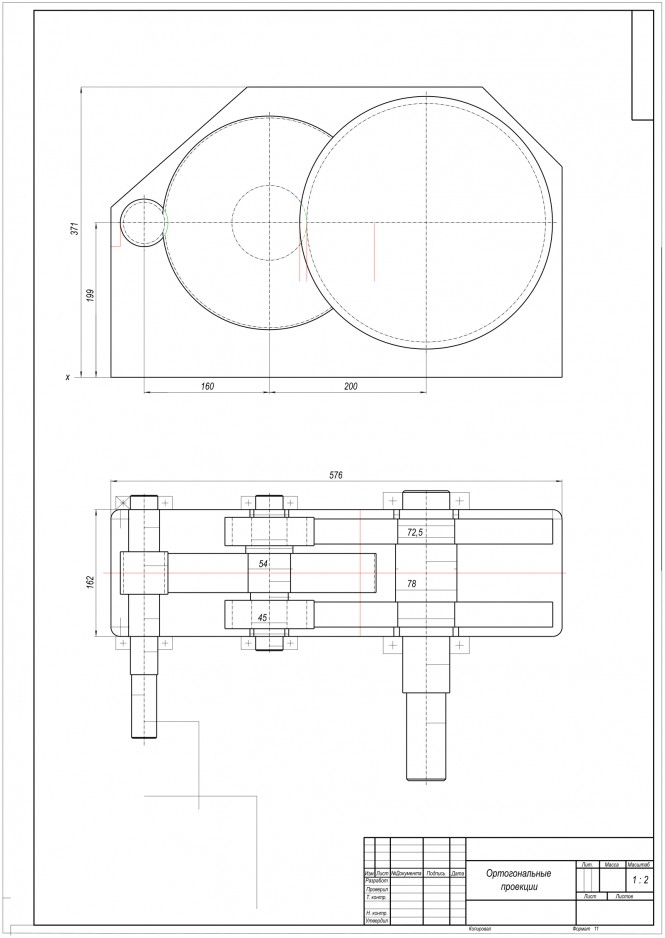
Начертить три вида детали. Главный вид взять по стрелке А. выполнить необходимые разрезы. Проставить размеры. 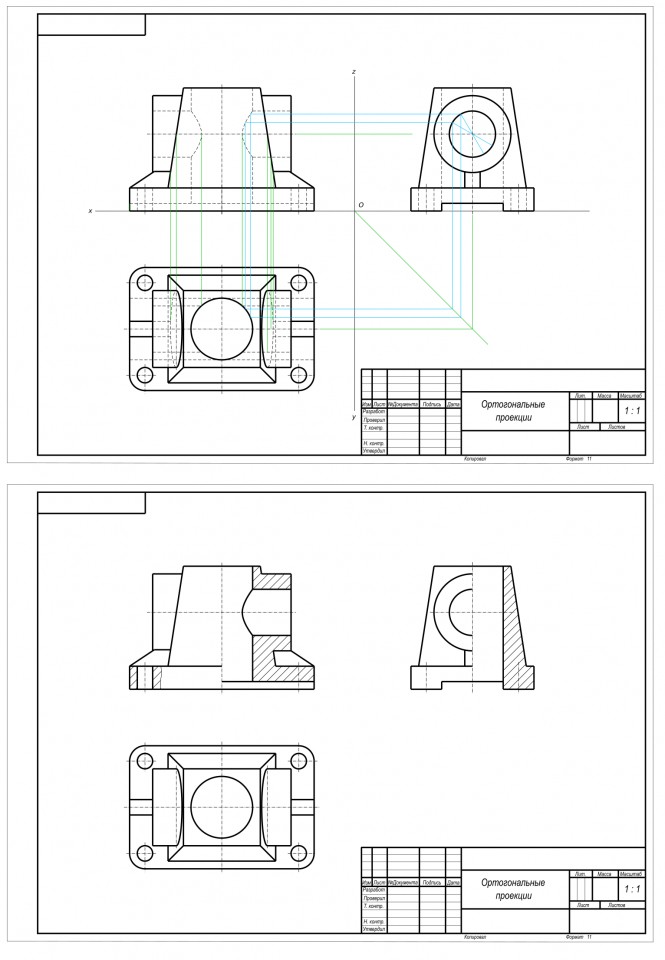
Начертить три вида детали. Главный вид взять по стрелке А. выполнить необходимые разрезы. Проставить размеры. КомментарииПостроить горизонтальную и профильную проекции призмы с вырезом
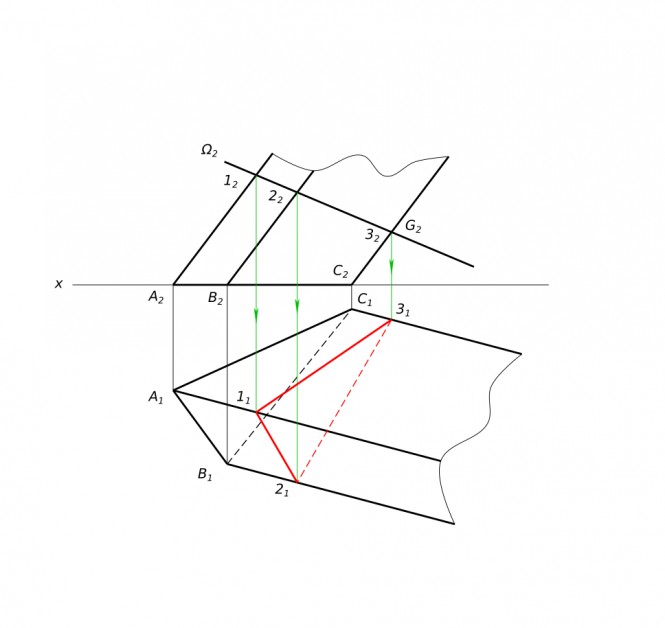
Построить горизонтальную и профильную проекции призмы с вырезом КомментарииПостроить линию пересечения поверхности наклонной призмы плоскостью Ω(Ω2)
Построить линию пересечения поверхности наклонной призмы плоскостью Ω(Ω2) КомментарииНайти центр описанной окружности О в плоскости ABC
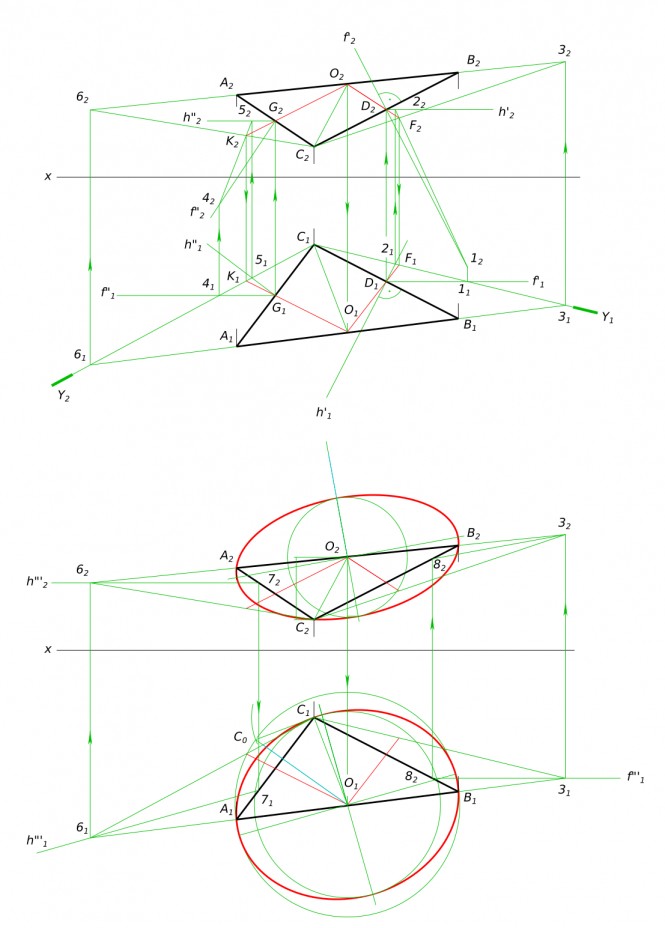
Найти центр описанной окружности О в плоскости ABC КомментарииОпустить перпендикулярно из точки А на прямую I
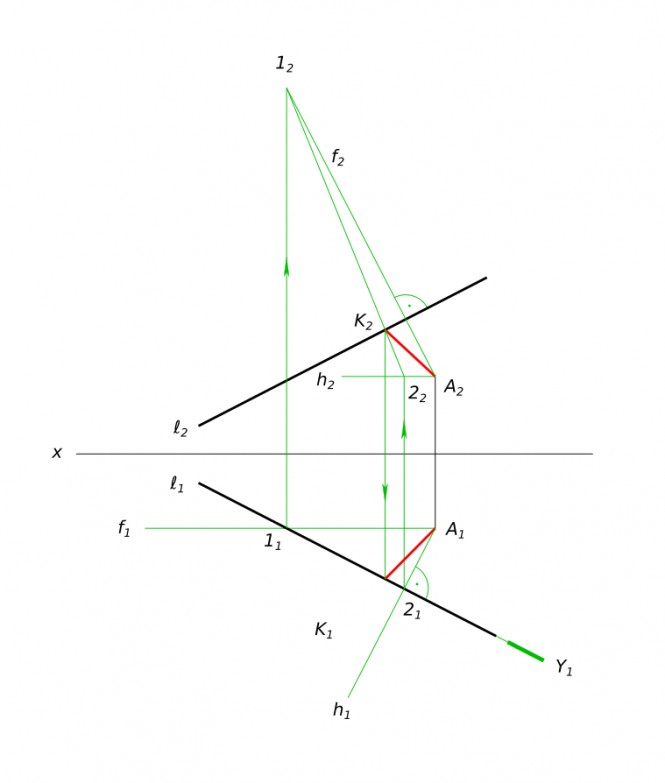
Опустить перпендикулярно из точки А на прямую I КомментарииПостроить проекции прямой I параллельной плоскости BCD
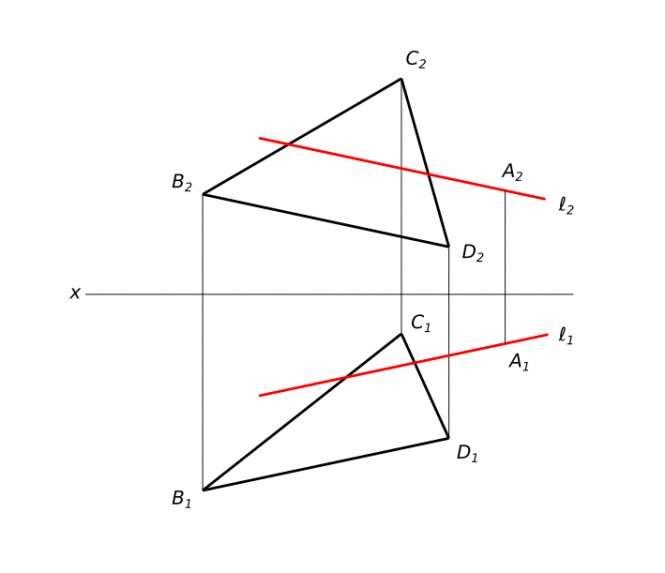
Построить проекции прямой I ∈ A, параллельной плоскости Σ(∆BCD)Построить проекции прямой I параллельной плоскости BCD КомментарииПровести перпендикуляр к прямой m из ее точки А до пересечения его с прямой I
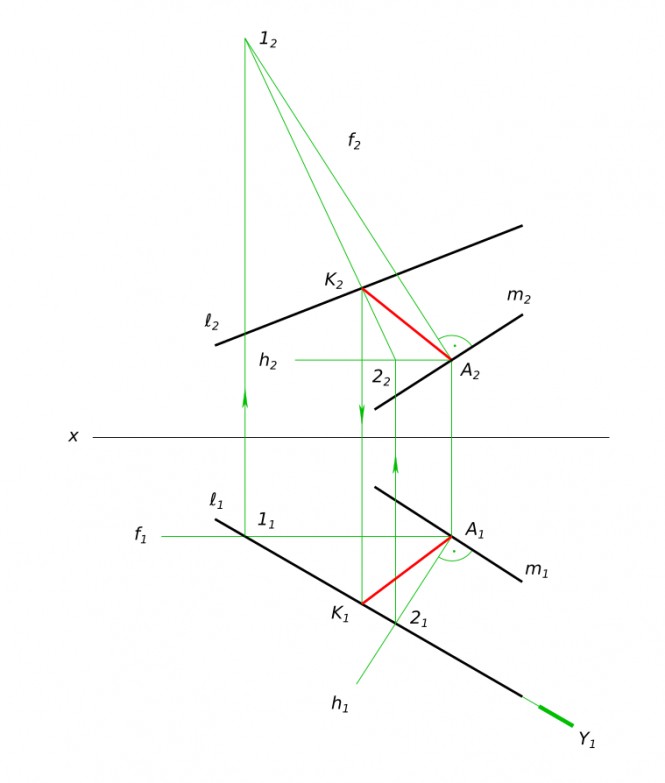
Провести перпендикуляр прямой m из ее точки А до пересечения его с прямой I КомментарииКомпоновочная схема редуктора
Спроектировать привод цепного конвейера Компоновочная схема редуктора После определения диаметров ступеней валов, расстояний между деталями передачи, после выбора типа подшипников и схемы их установки приступаем к вычерчиванию редуктора Компоновочную схему выполняем в масштабе 1:1 на миллиметровой бумаге. Для получения представления о конструкции, размерах деталей передач и их относительном расположении достаточно двух проекций. Для вычерчивания эскизной компоновки предварительно принимаем: длину ступицы цилиндрического колеса
$ ℓ_{ст} ≥ b_{2}; $ длину посадочного конца вала
$ ℓ_{МБ} = ℓ_{МТ} = 1,5d; $ длину промежуточного участка тихоходного вала
$ ℓ_{КТ} = 1,2d_{П}; $ длину промежуточного участка быстроходного вала
$ ℓ_{КБ} = 1,4d_{П}. $ Окончательные размеры ℓ_{ст} выявляем после расчета шпоночного (шлицевого) соединения или после подбора посадок с натягом. Окончательные размеры ℓ_{КБ} и ℓ_{КТ} определяем при конструировании крышек подшипников, после выбоа типа уплотнения и при конструировании корпусной детали. Окончательные размеры ℓ_{МБ} и ℓ_{МТ} получаем после выбора муфты, размеров звездочки, расчета шпоночного (шлицевого) соединения. Цилиндрические редукторы обычно конструируют с раземом корпуса по осям валов. Для этого последние располагают в одной плоскости. Такое исполнение наиболее удобно для сборки редуктора. Каждый из валов редуктора с опорами и со всеми расположенными на нем деталями можно собрать независимо от других валов и затем поставить в корпус. При необходимости осмотра и ремонта любой комплект вала может быть изъят из корпуса. Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил КомментарииИз заданного центра S спроектировать треугольник ABC на горизонтальную плоскость проекций
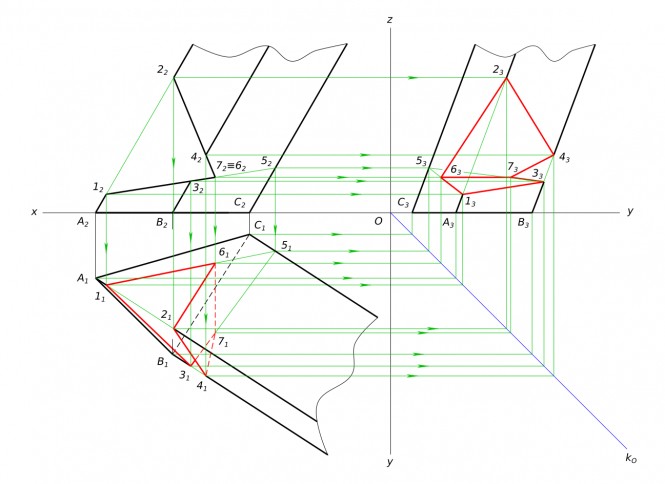
Из заданного центра S спроектировать треугольник ABC на горизонтальную плоскость проекций П1. Известны центральные проекции A1 и B1 вершин A и B треугольника и точка K пересечения прямой линии стороны AC этого треугольника с плоскостью проекций П1. 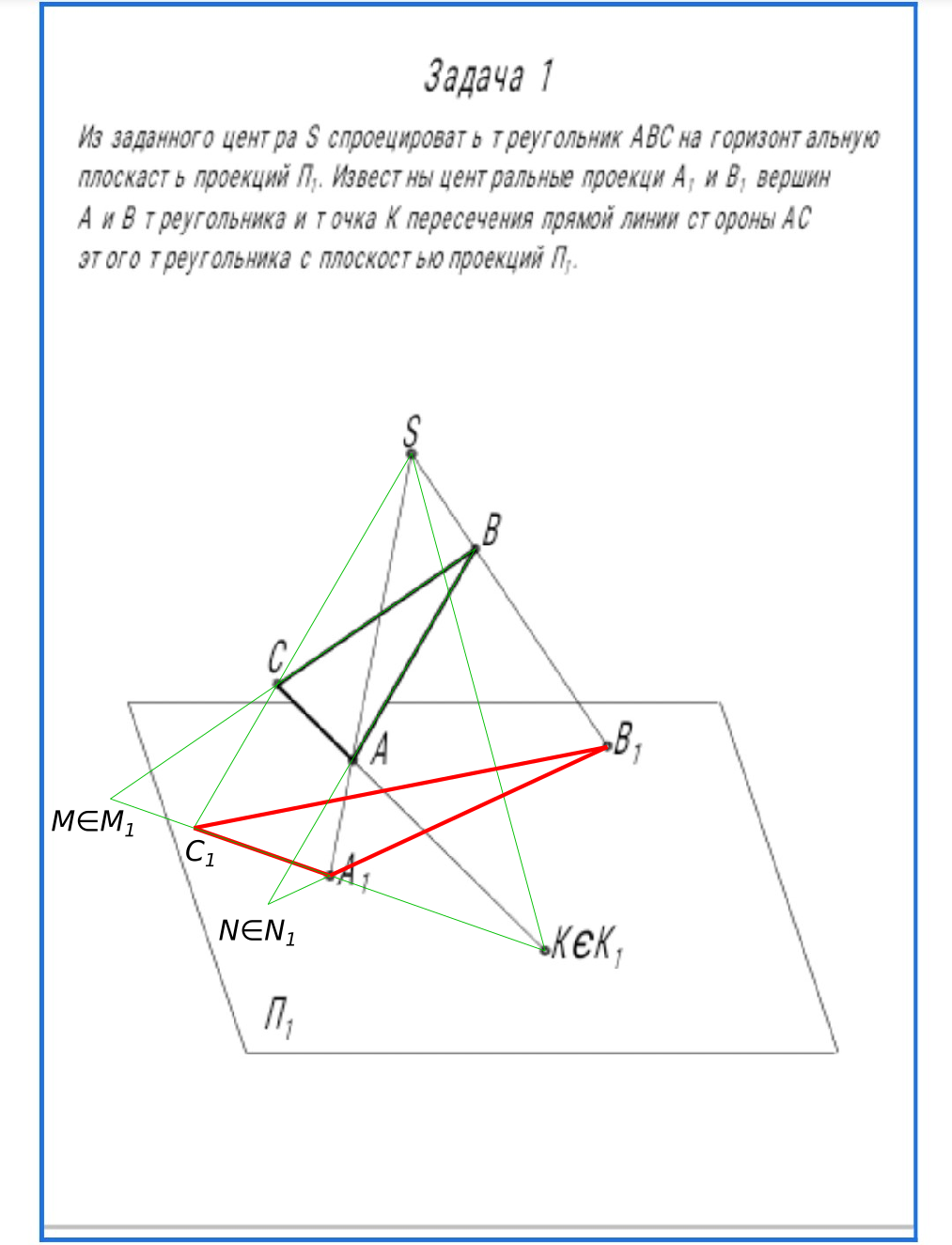
Из заданного центра S спроектировать треугольник ABC на горизонтальную плоскость проекций КомментарииВыбор типа подшипника
Выбор типа подшипника в соответствии с установившейся практикой проектироания и эксплуатации машин осуществляют по следующим рекомендациям. Для опор валов цилиндрических прямозубых и косозубых колес редукторов и коробок передач применяют чаще всего шариковые радиальные подшипники. 
Выбор типа подшипника Первоначально назначают подшипники серии диаметров 2. Если при последующем расчете грузоподъемность подшипника окажется недостаточной, то принимают подшипники серии диаметров 3. При чрезмерно больших размерах шариковых подшипников в качестве опор валов цилиндрических колес применяют подшипники конические роликовые. Предварительно назначаем шариковые радиальные подшипники легкой серии №207, №207 и №212. Обычно используют подшипники класса точности 0 (нормальный). Подшипники более высокой точности применяют для опор валов, требующих повышенной точности вращения или работающих при особо высоких чаcтотах вращения. [1, стр. 47] Устанавливаем подшипники по схеме 2а 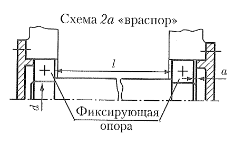
Выбор типа подшипника В большинстве случаев валы должны быть зафиксированы в опорах от осевых и рад перемещений. В следствии увеличения длины вала от температурных изменений осевые за зо ры в подшипниках схемы 2а, также уменьшаются. Чтобы не происходило защемление вала в опорах, предусматривают при сборке осевой за а. Принимаем
$ a = 0,5 мм $ КомментарииРасстояния между деталями передачи
Чтобы поверхности вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляют зазор "а" (мм) [1, стр.48]: 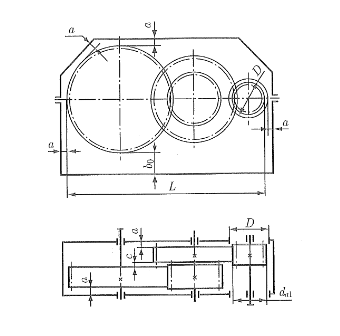
Расстояния между деталями передачи Расстояние
$ a = (L+3)^{1/3} = $
$ = (\frac{322,66}{2}+200+160+\frac{60,59}{2}+3)^{\frac{1}{3}} = 8,22 мм $ где L=551,63 - расстояние между внешними поверхностями деталей передач, мм. Принимаем
$ a = 12 мм $ Расстояние b0 между дном корпуса и поверхностью колес или червяка для всех типов редукторов и коробок передач принимают [1, стр. 48]:
$ b_{0} ≥ 3a $ Расстояние c между торцовыми поверхностями колес двухступенчатого редуктора, выполненного по развернутой схеме, принимают
$ c = (0,3...0,5)a = 0,5a = 0,5 × 12 = 6 мм $ Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил. КомментарииПодбор шпоночных соединений
Подбор шпоночных соединений Подбор шпонки для соединения зубчатого колеса и промежуточного вала При установке колес на валах необходимо обеспечить надежное базирование колеса по валу, передачу вращающего момента от колеса к валу или от вала к колесу. [1, стр. 81] Для передачи вращающего момента чаще всего применяют призматические и сегментные шпонки. 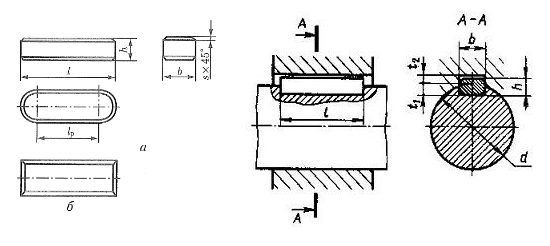
Подбор шпоночных соединений Призматические шпонки имеют прямоугольное сечение; концы скругленные (рис. а) или плоские (рис. б). Стандарт предусматривает для каждого диаметра вала определенные размеры поперечного сечения шпонки. Поэтому при проектных расчетах размеры b и h берут из табл. 9 [1, табл. 24.29] и определяют расчетную длину lр шпонки. Длину l = lр + b шпонки со скругленными или l = lр с плоскими торцами выбираем из стандартного ряда (табл. 9). Длину ступицы назначают на 8...10 мм больше длины шпонки. Назначаем в качестве соединения призматическую шпонку со скругленными концами. Длину l (мм) призматической шпонки выбирают из ряда: 10, 12, 14, 16, 18, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200, 250, 280. При диаметре вала 54 мм и длине ступицы 64,8 мм выбираем шпонку со следующими параметрами: b = 18 мм; h = 11 мм; s = 0.6 мм; t1 = 7 мм; t2 = 4.4 мм. Длину шпонки назначим примерно на 8...10 мм меньше длины ступицы, согласно стандартному ряду длин для шпонок: l = 50 - 200 мм. l = 56 мм При передаче момента шпоночным соединением посадки можно принимать по следующим рекомендациям (посадки с большим натягом - для колес реверсивных передач) [1, стр. 77]: Назначаем посадку шпоночного соединения H7/r6. Посадки шпонок регламентированы ГОСТ 23360-78 для призматических шпонок. Рекомендуют принимать поле допуска для ширины шпоночного паза вала для призматической шпонки P9, а ширины шпоночного паза отверстия P9. Подбор шпонки для соединения зубчатого колеса и выходного вала Назначаем в качестве соединения призматическую шпонку со скругленными концами. При диаметре вала 72.5 мм и длине ступицы 65 выбираем шпонку со следующими параметрами: b = 22 мм; h = 14 мм; s = 0.8 мм; t1 = 9 мм; t2 = 5.4 мм. Длину шпонки назначим примерно на 8...10 мм меньше длины ступицы, согласно стандартному ряду длин для шпонок: l = 56 - 220 мм. l = 56 мм. При передаче момента шпоночным соединением посадки можно принимать по следующим рекомендациям (посадки с большим натягом - для колес реверсивных передач) [1, стр. 77]: Назначаем посадку шпоночного соединения H7/r6. Посадки шпонок регламентированы ГОСТ 23360-78 для призматических шпонок. Рекомендуют принимать поле допуска для ширины шпоночного паза вала для призматической шпонки P9, а ширины шпоночного паза отверстия P9. Подбор шпонок входного и выходного хвостовиков Входной вал. При диаметре хвостовика 32 мм и длине хвостовика 80 мм выбираем шпонку со следующими параметрами: b = 10 мм; h = 8 мм; s = 0,4 мм; t1 = 5 мм; t2 = 3,3 мм; l = 22 - 110 мм. Длину шпонки назначим примерно на 8...10 мм меньше длины хвостовика, согласно стандартному ряду длин для шпонок: l = 70 мм. Выходной вал. При диаметре хвостовика 50 мм и длине хвостовика 110 мм выбираем шпонку со следующими параметрами: b = 18 мм; h = 11 мм; s = 0,4 мм; t1 = 7 мм; t2 = 4,4 мм; l = 50 - 200 мм. Длину шпонки назначим примерно на 8...10 мм меньше длины хвостовика, согласно стандартному ряду длин для шпонок: l = 100 мм. Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил. КомментарииПредварительный расчет валов
Предварительный расчет валов выполняем по вращающему моменту После определения меж осевых расстояний и размеров колес приступаем к разработке конструкции редуктора или коробки передач. На первом этапе конструирования осуществляем разработку компоновочной схемы. При этом определяем расположение деталей передачи, расстояния между ними, ориентировочные диаметры валов ступеней, выбираем типы подшипников и схемы их установки. 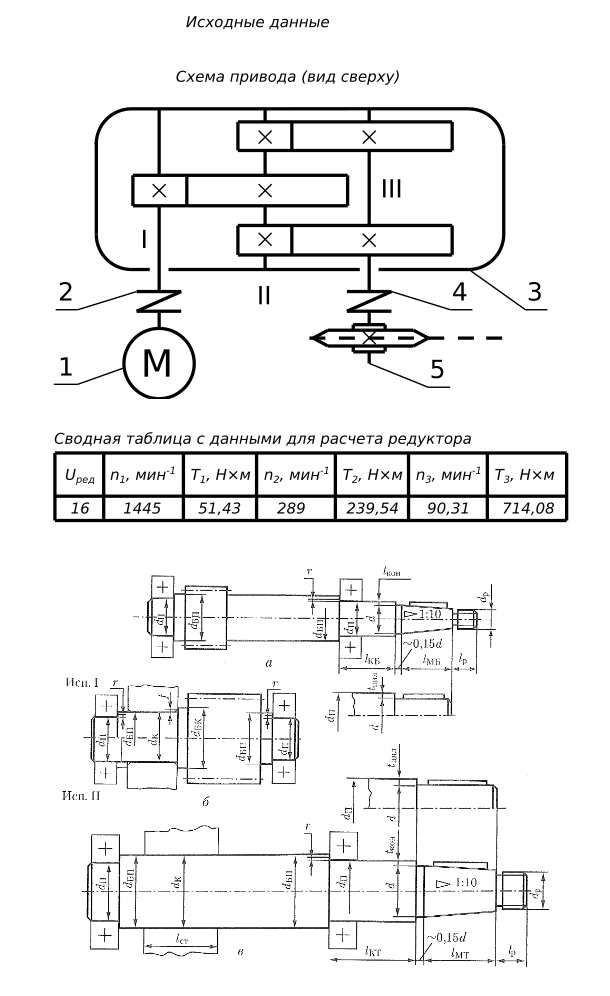
Предварительный расчет валов Эскизное проектирование После определения меж осевых расстояний, размеров колес приступаем к разработке конструкции редуктора. Первым этапом конструирования является разработка эскизного проекта. При эскизном проектировании определяют положение деталей передач, расстояния между ними, ориентировочные диаметры ступенчатых валов, выбирают типы подшипников и схемы их установки. [1, стр. 42] для быстроходного (входного) вала
$ d ≥ (7...8)(T_{Б})^{\frac{1}{3}} = (7...8)(51,43)^{\frac{1}{3}} = 29,75 мм $ для промежуточного
$ d_{к} ≥ (6...7)(T_{ПР})^{\frac{1}{3}} = (6...7)(239,54)^{\frac{1}{3}} = 45 мм $ для тихоходного (выходного)
$ d ≥ (6...7)(T_{Т})^{\frac{1}{3}} = (6...7)(714,08)^{\frac{1}{3}} = 50 мм $ Принимаем диаметры и длины концов согласно таблице 24.28 [1]
$ d_{вх}=32 мм; $
$ d_{вых}=50 мм $ Диаметры под подшипники:
$ d_{П_{вх}} = d_{П_{вх}}+2×t_{цил} = 28 + 2×3,5 = 35 мм; $
$ d_{П_{пр}} = d_{к}-3r = 45 - 3×3 = 36 мм; $
$ d_{П_{вых}} = d_{П_{вых}}+2×t_{цил} = 50 + 2×4 = 58 мм $ Высоту tцил(tкон) заплечника, координату r фаски подшипника и размер f (мм) фаски колеса принимают в зависимости от диаметра d [1, стр. 42]. Принимаем посадочные места под подшипники согласно ГОСТ 8338-75 на подшипники шариковые радиальные однорядные (табл. 24.10 [1]):
$ d_{П_{вх}} = 35 мм; $
$ d_{П_{пр}} = 35 мм; $
$ d_{П_{вых}} = 60 мм $ Диаметры без контактных поверхностей
$ d_{БП вх} = d_{П}+3r= 35 + 3×1,5 = 39,5 мм; $
$ d_{БП пр} = 35 + 3×2,5 = 42,5 мм; $
$ d_{БП вых} = 60 + 3×3,5 = 70,5 мм $ Принимаем диаметр выходного (тихоходного) вала для установки зубчатого колеса:
$ d_{К вых} = 72,5 мм $ Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Проверка зубьев колес по контактным напряжениям Расчетное значение контактного напряжения [1, стр. 23]
$ σ_{H} =\frac{Z_{σ}}{a_{W}}(\frac{K_{H}T_{1}(u_{ф}±1)^{3}}{(b_{1}u_{ф})})^{\frac{1}{2}}≤[σ]_{H}=482,8 МПа $ где Zσ = 9600 для прямозубых и Zσ = 8400 для косозубых передач, МПа^{1/2}
$ σ_{H} = \frac{8400}{200}(\frac{1,3218×239,54(3,1956+1)^{3}}{(2×32×3,1956)})^{\frac{1}{2}}=449,1 МПа $ Если расчетное напряжение σH меньше допустимого [σ]H в пределах 15-20% или σH больше [σ]H в пределах 5%, то ранее принятые параметры передачи принимают за окончательные. В противном случае необходим пересчет. [1, стр. 23] σH (больше) меньше [σ]H на 6,51%. Ранее принятые параметры передачи принимаем за окончательные. Силы в зацеплении 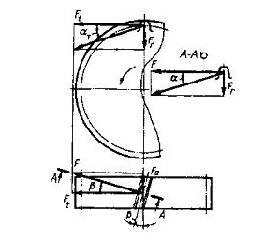
Расчет зубчатых колес Окружная
$ F_{t} = \frac{2×10^{3}×T_{1}}{d_{1}} = \frac{2×10^{3}×239,54}{95,34} = 5025 Н $ радиальная (для стандартного угла α=20o tgα=0,364)
$ F_{r} = \frac{F_{t}tgα}{cosβ} = \frac{5025 × 0,364}{0,965} = 1895 Н $ осевая
$ F_{a} = F_{t}tgβ = 5025 × 0,2717 = 1365 Н $ Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Диаметры колес 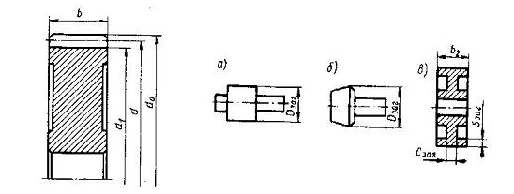
Расчет зубчатых колес Делительные диаметры d [1, стр. 22]: шестерни
$ d_{1} = \frac{z_{1}m}{cosβ} = \frac{46×2}{0,965} = 95,34 мм $ колеса внешнего зацепления
$ d_{2} = 2a_{W} - d_{1}=2×200-95,34=304,66 мм $ Диаметры da и df окружностей вершин и впадин зубьев колес внешнего зацепления [1, стр. 22]:
$ d_{a_{1}} = d_{1} + 2(1 + x_{1} - y)m; $
$ d_{f_{1}} = d_{1} - 2(1,25 - x_{1})m; $
$ d_{a_{2}} = d_{2} + 2(1 + x_{2} - y)m; $
$ d_{f_{2}} = d_{2} - 2(1,25 - x_{2})m $ где x1 и x2 - коэффициенты смещения у шестерни и колеса; коэффициент воспринимаемого смещения
$ y = \frac{-(a_{W} - a)}{m} $ делительное меж осевое расстояние:
$ a = 0,5m(z_{2} ± z_{1}) = 0,5 × 2 × (147+46) = 193 мм $
$ y = \frac{-(200 - 193)}{2} = -3,5 $
$ d_{a_{1}} = 95,34 + 2 × [1-(-3,5)] × 2 = 113,34 мм $
$ d_{f_{1}} = 95,34 - 2 × 1,25 × 2 = 90,34 мм $
$ d_{a_{2}} = 304,66 + 2 × [1-(-3,5)] × 2 = 322,66 мм $
$ d_{f_{2}} = 304,66 - 2 × 1,25 × 2 = 299,66 мм $ Размеры заготовок Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры Dзаг, Cзаг, Sзаг заготовок колес не превышали предельно допустимых значений Dпр, Sпр (табл. 1 [1, табл. 2.1, стр. 11]) [1, стр. 22]: Dзаг ≤ Dпр; Cзаг ≤ Cпр; Sзаг ≤ Sпр. Значения Dзаг, Cзаг, Sзаг (мм) вычисляются по формулам:
$ D_{заг} = d_{a} + 6 мм $ для колеса с выточками
$ C_{заг} = 0,5b_{2} и S_{заг} = 8m $ для колеса без выточек
$ S_{заг} = b_{2} + 4 мм $
$ D_{заг_{1}} = 113,34 + 6 мм = 119,34 мм $
$ D_{заг_{2}} = 322,66 + 6 мм = 328,66 мм $
$ S_{заг_{2}} = 32 + 4 мм = 36 мм $ КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Вычисленное значение меж осевого расстояния округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra 40 [1, табл. 24.1]. При крупносерийном производстве редукторов aw округляют до ближайшего стандартного значения: 50; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400 мм. [1, стр. 20] Принимаем
$ a_{W} = 200 мм $ Предварительные основные размеры колеса: Делительный диаметр
$ d_{2} = \frac{2a_{W}u}{u ± 1}=\frac{2×200×3,2}{3,2 + 1}=304,76 мм $ Ширина
$ b_{2} = ψ_{ba} × a_{W}= 0,31 × 200 = 62 мм $ Принимаем выбранное из стандартного ряда Ra 40 значение ширины:
$ b_{2} = 32+32 мм $ Модуль передачи Максимально допустимый модуль mmax, мм, определяют из условия неподрезания зубьев у основания [1, стр. 20]
$ m_{max} ≈ \frac{2a_{W}}{17(u ± 1)}=\frac{2 ×200}{17(3,2 + 1)} = 5,60 мм $ Минимальное значение модуля mmin, мм, определяют из условия прочности [1, стр. 20]:
$ m_{min}=\frac{K_{m}K_{F}T_{1}(u±1)}{a_{W}b_{2}[σ]_{F}} $ где Km = 3,4 × 103 для прямозубых и Km = 2,8 × 103 для косозубых передач; вместо [σ]F подставляют меньшее из значений [σ]F2 и [σ]F1. Табл. 8 [1, табл. 2.9, стр. 20] Коэффициент нагрузки при расчете по напряжениям изгиба
$ K_{F} = K_{F_{ν}}K_{F_{β}}K_{F_{α}} $ Коэффициент KFν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления шестерни и колеса. Значения KFν принимают по табл. 8 [1, табл. 2.9, стр. 20] в зависимости от степени точности по нормам плавности, окружной скорости и твердости рабочих поверхностей. Для степени точности 9, максимальной окружной 1,02 м/с, твердости HB≤350 принимаем
$ K_{F_{ν}}=1,11 $ KFβ - коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца, оценивают по формуле
$ K_{F_{β}}=0,18+0,82K^{0}_{H_{β}} $ KFα - коэффициент, учитывающий влияние погрешности изготовления шестерни и колеса на распределение нагрузки между зубьями, определяют так же как при расчетах на контактную прочность:
$ K_{F_{α}} = K^{0}_{F_{α}} $ В связи с менее благоприятным влиянием приработки на изгибную прочность, чем на контактную, и более тяжелыми последствиями из-за неточности при определении напряжений изгиба приработку зубьев при вычислении коэффициентов KFβ и KFα не учитывают. [1, стр. 21]
$ K_{F} = K_{F_{ν}} = 1,11 $
$ m_{min} =\frac{2,8 × 10^{3}×1,11×239,54(3,2+1)}{200×62×181,06}= 1,39 мм $ Из полученного диапазона (mmin=1,48...mmax=5,60) модулей принимают меньшее значение m, согласуя его со стандартным (ряд 1 следует предпочитать ряду 2) [1, стр. 21]: Ряд 1, мм ..... 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0; 8,0; 10,0 Ряд 2, мм ..... 1,12; 1,37; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7,0; 9,0 Принимаем из стандартного ряда модуль
$ m = 2 мм $ Значения модулей m < 1 при твердости ≤ 350 HB и m Минимальный угол наклона зубьев косозубых колес [1, стр. 21]
$ β_{min} = arcsin(\frac{4m}{b_{2}})=arcsin(\frac{4×2}{32})=14,48° $ Суммарное число зубьев
$ z_{s} = \frac{2a_{W}cosβ_{min}}{m} = \frac{2×200×0,9682}{2} = 193,65 $ Полученное значение zs округляют в меньшую сторону до целого числа
$ z_{s} = 193 $ Определяют действительное значение угла β наклона зуба:
$ β = arccos[\frac{z_{s}m}{2a_{W}}]=arccos[\frac{193 × 2}{2×200}] = 15,20° $ Справочно: для косозубых колес β = 8...20°, для шевронных - β = 25...40°. Число зуьев шестерни и колеса Число зубьев шестерни [1, стр. 21]
$ z_{1} = \frac{z_{s}}{(u ± 1)} ≥ z_{1_{min}} $
$ z_{1} = \frac{193}{(3,2 + 1)} = 45,95 $ Значение z1 округляют в ближайшую сторону до целого числа. [1, стр. 21]
$ z_{1} = 46 $ Число зубьев колеса внешнего зацепления:
$ z_{2} = z_{s} - z_{1} = 193 - 46 = 147 $ Фактические значения передаточных чисел не должны отличаться от номинальных более чем на: 3% - для одноступенчатых, 4% - для двухступенчатых и 5% - для многоступенчатых редукторов. [1, стр. 22] Отклонение от номинального передаточного числа
$ Δ = \frac{(u - u_{ф})}{u} = \frac{3,2-3,1957}{3,2}= 0,13 % $ КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Коэффициент YA учитывает влияние двустороннего приложения нагрузки (реверса). При одностороннем приложении нагрузки YA = 1. При реверсивном нагружении и одинаковых нагрузке и числе циклов нагружения в прямом и обратном направлении (например, зубья сателлита в планетарной передаче): Y_{A} = 0,65 для нормализованных и улучшенных сталей; Y_{A} = 0,75 для закаленных и цементованных; Y_{A} = 0,9 для азотированных Так как в проектируемой передаче (не)планируется реверсивный ход, то с учетом ТО принимаем: для шестерни (улучшение и закалка ТВЧ)
$ Y_{A_{1}} = 0,75 $ для колеса (улучшение)
$ Y_{A_{2}} = 0,65 $ Для шестерни:
$ [σ]_{F_{1}} = \frac{[σ]_{F_{lim_{1}}}Y_{N_{ш}}Y_{R}Y_{A_{1}}}{S_{F_{1}}} = \frac{600×1×1,1×0,75}{1,7}=291,18 МПа $ Для колеса:
$ [σ]_{F_{2}} = \frac{[σ]_{F_{lim_{2}}}Y_{N_{кол}}Y_{R}Y_{A_{2}}}{S_{F_{2}}} = \frac{431×1×1,1×0,65}{1,7}=181,06 МПа $ Проектный расчет Меж осевое расстояние Предварительное значение меж осевого расстояния a'w мм:
$ a'_{W}=K(u±1)(\frac{T_{1}}{u})^{\frac{1}{3}} $ где знак "+" (в скобках) относят к внешнему зацеплению, знак "-" - к внутреннему; T1 - вращающий момент на шестерне (наибольший из длительно действующих), Н×м; u - передаточное число. Коэффициент K в зависимости от поверхностной твердости H1 и H2 зубьев шестерни и колеса соответственно имеет следующие значения [1, стр. 17]: Поверхностная твердость и шестерни до 480 HB и колеса до 262 HB, поэтому принимаем коэффициент
$ K = 8 $ передаточное число
$ U = 3,2 $
$ a'_{W} = 8(3,2±1)(\frac{239,54}{3,2})^{\frac{1}{3}}=141,6 мм $ Окружную скорость ν, м/с, вычисляют по формуле:
$ ν=\frac{2πa'_{W}n_{1}}{(6×10^{4}(u±1))}=\frac{2π×141,6×291}{(6×10^{4}(3,2±1))}=1,02 м/с $ Степень точности зубчатой передачи назначают по табл. 4 [1, табл. 2.5, стр. 17]: При окружной скорости 1,02 м/с (что меньше 6 м/с) выбираем степень точности 9. Уточняем предварительно найденное значение меж осевого расстояния:
$ a_{W}=K_{a}(u±1)(\frac{K_{H}T_{1}}{ψ_{ba}u[σ]^{2}_{H}})^{\frac{1}{3}} $ где Ka = 450 - для прямозубых колес; Ka = 410 - для косозубых и шевронных, МПа; [σ]H - в МПа. ψba - коэффициент ширины принимают из ряда стандартных чисел: 0,1; 0,15; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63 в зависимости от положения колес относительно опор: при симметричном расположении 0,315-0,5; при несимметричном 0,25-0,4; при консольном расположении одного или обоих колес 0,25-0,4; Для шевронных передач ψba = 0,4 - 0,63; для коробок передач ψba = 0,1 - 0,2; для передач внутреннего зацепления ψba = 0,2 (u+1)/(u-1). Меньшие значения ψba - для передач с твердостью зубьев H ≥ 45HRC. Принимаем
$ ψ_{ba} = 0,31 $ Коэффициент нагрузки в расчетах на контактную прочность
$ K_{H} = K_{H_{ν}}K_{H_{β}}K_{H_{α}} $ Коэффициент KHν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса. Значения KHν принимают по табл. 5 в зависимости от степени точности передачи по нормам плавности, окружной скорости и твердости рабочих поверхностей. Табл. 5 [1, табл. 2.6, стр. 18] Примечание. В числителе приведены значения для прямозубых, в знаменателе - для косозубых зубчатых колёс. Для степени точности 9, максимальной окружной скорости 1.02 м/с, твердости HB≤350 принимаем
$ K_{H_{ν}} = 1,06 $ Коэффициент KHβ учитывает неравномерность распределения нагрузки по длине контактных линий, обусловливаемую погрешностями изготовления (погрешностями направления зуба) и упругими деформациями валов, подшипников. Зубья зубчатых колес могут прирабатываться: в результате повышенного местного изнашивания распределение нагрузки становится более равномерным. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы K0Hβ и после приработки KHβ. Значение коэффициента K0Hβ принимают по таблице 6 в зависимости от коэффициента ψbd = b2/d1, схемы передачи и твердости зубьев. Так как ширина колеса и диаметр шестерни еще не определены, значение коэффициента ψbd вычисляют ориентировочно:
$ ψ_{bd} = 0,5ψ_{ba} (u ± 1) = 0,5 × 0,31 × (3,2 + 1) = 0,651 $ Коэффициент KHβ определяют по формуле:
$ K_{H_{β}} = 1 + (K^{0}_{H_{β}} - 1)K_{H_{w}} $ где KHw - коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7). Коэффициент KHα определяют по формуле:
$ K_{H_{α}} = 1 + (K^{0}_{H_{α}} - 1)K_{H_{w}} $ где KHw - коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7). Начальное значение коэффициента K0Hα распределения нагрузки между зубьями в связи с погрешностями изготовления (погрешностями шага зацепления и направления зуба) определяют в зависимости от степени точности (nст = 5, 6, 7, 8, 9) по нормам плавности: для прямозубых передач K^{0}_{H_{α}} = 1 + 0,06(n_{ст} - 5), при условии 1 ≤ K^{0}_{H_{α}} ≤ 1,25; K^{0}_{H_{α}} = 1 + A(n_{ст} - 5), при условии 1 ≤ K^{0}_{H_{α}} ≤ 1,6, для косозубых передач где A = 0,15 - для зубчатых колес с твердостью H1 и H2 > 350 HB и A = 0,25 при H1 и H2 ≤ 350 HB или H1 > 350 HB и H2 ≤ 350 HB
$ K^{0}_{H_{α}} = 1 + 0,06(9 - 5) = 1,24 $ Принимаем коэффициент KHw по табл. 7 равным (ближайшее значение твердости по таблице 250 HB или 23 HRC к твердости колеса 262 HB) 0,28
$ K_{H_{α}} = 1 + (1,24 - 1)0,28 = 1,0672 $ Принимаем коэффициент K0Hβ по табл. 6 (схема 3) равным 1,02
$ K_{H_{β}} = 1 + (1,02 - 1) 0,28 = 1,0052 $
$ K_{H} = K_{H_{ν}}K_{H_{β}}K_{H_{α}}= 1,06 × 1,0052 × 1,0672 = 1,32 $ Уточнённое значение меж осевого расстояния:
$ a_{W} =450(3,2±1)(\frac{1,32×239,54}{0,31×3,2×(482,82)^{2}})1/3= 209,84 мм $ КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Коэффициент ZV учитывающий влияние окружной скорости V, принимаем как для шестерни так и для колеса и удовлетворяющий в большинстве случаев
$ Z_{V}=1,05 $ Для шестерни:
$ [σ]_{H_{1}} = \frac{[σ]_{H_{lim}}Z_{N_{ш}}Z_{R}Z_{V}}{S_{H}}=\frac{1016×1×0,9×1,05}{1,2}=800,1 МПа $ Для колеса:
$ [σ]_{H_{2}} = \frac{[σ]_{H_{lim}}Z_{N_{кол}}Z_{R}Z_{V}}{S_{H}}=\frac{562×1×0,9×1,05}{1,1}=482,8 МПа $ Допускаемое напряжение [σ]H для цилиндрических и конических передач с прямыми зубьями равно меньшему из допускаемых напряжений шестерни [σ]H1 и колеса [σ]H2
$ [σ]_{H} = 482,8 МПа $ Определение напряжений изгиба Допускаемые напряжения изгиба зубьев шестерни [σ]F1 и колеса [σ]F2 определяют по общей зависимости (но с подстановкой соответсвующих параметров для шестерни и колеса), учитывая влияние на сопротивление усталости при изгибе долговечности (ресурса), шероховатости поверхности выкружки (переходной поверхности между смежными зубьями) и реверса (двустороннего приложения) нагрузки: Предел прочности [σ]Flim при отнулевом цикле напряжений вычисляют по эмпирическим формулам. 1. табл. 2.3
$ [σ]_{F} =\frac{[σ]_{F_{lim}}Y_{N}Y_{R}Y_{A}}{S_{F}} $ Принимаем для выбранной марки стали и ТО (Сталь 40Х, улучшение и закалка ТВЧ) шестерни
$ [σ]_{F_{lim 1}} = 600 МПа $ Для колеса (Сталь 40Х, улучшение)
$ [σ]_{F_{lim 2}} = 1,75 HB_{ср} = 1,75 × 246 = 431 МПа $ Минимальное значение коэффициента запаса прочности: для цементованных и нитроцементованных зубчатых колес - SF = 1,55; для остальных - SF = 1,7. Принимаем для шестерни (улучшение и закалка ТВЧ)
$ S_{F_{1} = 1,7 $ Для колеса (улучшение)
$ S_{F_{2}} = 1,7 $ Коэффициент долговечности YN учитывает влияние ресурса:
$ Y_{N} = (\frac{N_{F_{lim}}}{N_{k}})^{(\frac{1}{q})}, при условии 1≤Y_{N}≤Y_{N_{max}} $ Для закаленных и поверхностно упрочненных зубьев
$ Y_{N_{max}} = 2,5 и q = 9 $ Число циклов, соответствующее перегибу кривой усталости
$ N_{F_{lim}} = 4 × 10^{6} $ Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем
$ Y_{N_{max 1}} = 2,5 и q_{1} = 9 $ Для выбранной ТО колеса (улучшение) принимаем
$ Y_{N_{max 2}} = 2,5 и q_{2} = 9 $ Назначенный ресурс Nk вычисляют так же, как и при расчетах по контактным напряжениям. В соотеветствии с кривой усталости напряжения σF не могут иметь значений меньших σFlim. Поэтому при Nk > NFlim принимают Nk = NFlim. Для длительно работающих быстроходных передач Nk ≥ NFlim и, следовательно YN = 1, что и учитывает первый знак неравенства в (2). Второй знак неравенства ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба. Для шестерни:
$ N_{k_{ш}} = 60nn_{з}L_{h} = 60 × 291 × 1 × 19510 = 338308116 $ Т.к. Nk ш > NFG, то принимаем Nk ш = NFG = 4000000.
$ Y_{N_{ш}} = 1 $ Для колеса:
$ N_{k_{кол}} = 60 × 91 × 1 × 19510 = 105721286 $ Т.к. Nk кол > NFG, то принимаем Nk кол = NFG = 4000000
$ Y_{N_{кол}} = 1 $ Коэффициент YR, учитывающий влияние шероховатости переходной поверхности между зубьями, принимают: YR = 1 при шлифовании и зубофрезеровании с параметром шероховатости RZ ≤ 40 мкм; YR = 1,05...1,2 при полировании (большие значения при улучшении и после закалки ТВЧ). Принимаем
$ Y_{R} = 1,1 $ Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Проверка зубьев колес по контактным напряжениям Расчетное значение контактного напряжения [1, стр. 23]
$ σ_{H} =\frac{Z_{σ}}{a_{W}}(\frac{K_{H}T_{1}(u_{ф}±1)^{3}}{b_{1}u_{ф}})^{\frac{1}{2}}≤[σ]_{H}=482,8 МПа $ где Zσ = 9600 для прямозубых и Zσ = 8400 для косозубых передач, МПа^{1/2}
$ σ_{H} = \frac{9600}{160}(\frac{1,2342×51,43(5+1)^{3}}{50×5})^{\frac{1}{2}}=451,35 МПа $ Если расчетное напряжение σH меньше допустимого [σ]H в пределах 15-20% или σH больше [σ]H в пределах 5%, то ранее принятые параметры передачи принимают за окончательные. В противном случае необходим пересчет. [1, стр. 23] σH (больше) меньше [σ]H на 6,51%. Ранее принятые параметры передачи принимаем за окончательные. Силы в зацеплении 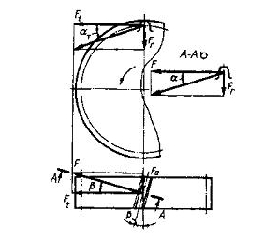
Расчет зубчатых колес Окружная
$ F_{t} = \frac{2×10^{3}×T_{1}}{d_{1}} = \frac{2×10^{3}×51,43}{52,5} = 2076 Н $ радиальная (для стандартного угла α=20o tgα=0,364)
$ F_{r} = \frac{F_{t}tgα}{cosβ} = \frac{2076 × 0,364}{1} = 756 Н $ осевая
$ F_{a} = F_{t}tgβ = 2075,81 × 0 = 0 Н $ Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Диаметры колес 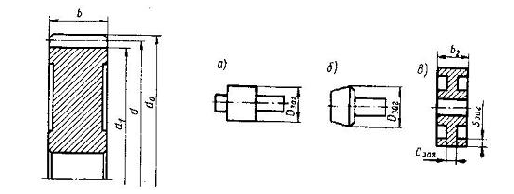
Расчет зубчатых колес Делительные диаметры d [1, стр. 22]: шестерни
$ d_{1} = \frac{z_{1}m}{cosβ} = \frac{30×1,75}{1} = 52,5 мм $ колеса внешнего зацепления
$ d_{2} = 2a_{W} - d_{1}=2×160-52,5=267,54 мм $ Диаметры da и df окружностей вершин и впадин зубьев колес внешнего зацепления [1, стр. 22]:
$ d_{a_{1}} = d_{1} + 2(1 + x_{1} - y)m; $
$ d_{f_{1}} = d_{1} - 2(1,25 - x_{1})m; $
$ d_{a_{2}} = d_{2} + 2(1 + x_{2} - y)m; $
$ d_{f_{2}} = d_{2} - 2(1,25 - x_{2})m; $ где x1 и x2 - коэффициенты смещения у шестерни и колеса; коэффициент воспринимаемого смещения
$ y = \frac{-(a_{W} - a)}{m}; $ делительное меж осевое расстояние:
$ a = 0,5m(z_{2} ± z_{1}) = 0.5 × 1.75 × (152+30) = 159,25 мм $
$ y = \frac{-(160 - 159,25)}{1,75} = -1,31 $
$ d_{a_{1}} = 52,5 + 2 × [1-(-1,31)] × 1,75 = 60,59 мм $
$ d_{f_{1}} = 52,5 - 2 × 1,25 × 1.75 = 48,13 мм $
$ d_{a_{2}} = 267,54 + 2 × [1-(-1,31)] × 1,75 = 271,58 мм $
$ d_{f_{2}} = 267,54 - 2 × 1,25 × 1.75 = 263,17 мм $ Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры Dзаг, Cзаг, Sзаг заготовок колес не превышали предельно допустимых значений Dпр, Sпр (табл. 1 [1, табл. 2.1, стр. 11]) [1, стр. 22]: Dзаг ≤ Dпр; Cзаг ≤ Cпр; Sзаг ≤ Sпр. Значения Dзаг, Cзаг, Sзаг (мм) вычисляются по формулам: для цилиндрической шестерни (рис. 3, а)
$ D_{заг} = d_{a} + 6 мм; $ для колеса с выточками (рис. 3, в)
$ C_{заг} = 0,5b_{2} и S_{заг} = 8m; $ для колеса без выточек (рис. 2)
$ S_{заг} = b_{2} + 4 мм $
$ D_{заг_{1}} = 60,59 + 6 мм = 66,66 мм; $
$ D_{заг_{2}} = 271,58 + 6 мм = 277,58 мм; $
$ S_{заг_{2}} = 50 + 4 мм = 54 мм $ КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Вычисленное значение межосевого расстояния округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra 40 [1, табл. 24.1]. При крупносерийном производстве редукторов aw округляют до ближайшего стандартного значения: 50; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400 мм. [1, стр. 20] Принимаем
$ a_{W} = 160 мм $ Предварительные основные размеры колеса: Делительный диаметр
$ d_{2} = 2a_{W}u/(u ± 1)=2×160×5/(5 + 1)=266,67 мм $ Ширина
$ b_{2} = ψ_{ba} × a_{W}= 0,31 × 160 = 49,6 мм $ Принимаем выбранное из стандартного ряда Ra 40 значение ширины:
$ b_{2} = 50 мм $ Модуль передачи Максимально допустимый модуль mmax, мм, определяют из условия неподрезания зубьев у основания [1, стр. 20]
$ m_{max} = \frac{2a_{W}}{17(u ± 1)}=\frac{2 ×160}{17(5 + 1)} = 3,14 мм $ Минимальное значение модуля mmin, мм, определяют из условия прочности [1, стр. 20]:
$ m_{min}=\frac{K_{m}K_{F}T_{1}(u±1)}{a_{W}b_{2}[σ]_{F}} $ где Km = 3,4 × 10^{3} для прямозубых и Km = 2,8 × 10^{3} для косозубых передач; вместо [σ]F подставляют меньшее из значений [σ]F2 и [σ]F1. Табл. 8 [1, табл. 2.9, стр. 20] Коэффициент нагрузки при расчете по напряжениям изгиба
$ K_{F} = K_{F_{ν}}K_{F_{β}}K_{F_{α}} $ Коэффициент KFν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления шестерни и колеса. Значения KFν принимают по табл. 8 [1, табл. 2.9, стр. 20] в зависимости от степени точности по нормам плавности, окружной скорости и твердости рабочих поверхностей. Для степени точности 9, максимальной окружной 2,68 м/с, твердости HB≤350 принимаем
$ K_{F_{ν}}=1,12 $ KFβ - коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца, оценивают по формуле
$ K_{F_{β}}=0,18+0,82K^{0}_{H_{β}} $ KFα - коэффициент, учитывающий влияние погрешности изготовления шестерни и колеса на распределение нагрузки между зубьями, определяют так же как при расчетах на контактную прочность:
$ K_{F_{α}} = K^{0}_{F_{α}} $ В связи с менее благоприятным влиянием приработки на изгибную прочность, чем на контактную, и более тяжелыми последствиями из-за неточности при определении напряжений изгиба приработку зубьев при вычислении коэффициентов KFβ и KFα не учитывают. [1, стр. 21]
$ K_{F} = K_{F_{ν}} = 1,12} $
$ m_{min} =\frac{3,4 × 10^{3}×1,12×51,43(5+1)}{160×50×181,27}= 0,83 мм $ Из полученного диапазона (mmin=0,83...mmax=3,14) модулей принимают меньшее значение m, согласуя его со стандартным (ряд 1 следует предпочитать ряду 2) [1, стр. 21]: Ряд 1, мм ..... 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0; 8,0; 10,0 Ряд 2, мм ..... 1,12; 1,37; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7,0; 9,0 Принимаем из стандартного ряда
$ m = 1,75 мм $ Значения модулей m < 1 при твердости ≤ 350 HB и m Минимальный угол наклона зубьев прямозубых колес [1, стр. 21]
$ β_{min} = 0° $ Суммарное число зубьев
$ z_{s} = \frac{2a_{W}cosβ_{min}}{m} = \frac{2×160×1}{1,75} = 181,03 $ Полученное значение zs округляют в меньшую сторону до целого числа и определяют действительное значение угла β наклона зуба:
$ z_{s} = 182 $ Число зубьев шестерни и колеса Число зубьев шестерни [1, стр. 21]
$ z_{1} = \frac{z_{s}}{(u ± 1)} ≥ z_{1_{min}} $
$ z_{1} = \frac{182}{(5 + 1)} = 30,33 $ Значение z1 округляют в ближайшую сторону до целого числа. [1, стр. 21]
$ z_{1} = 30 $ Число зубьев колеса внешнего зацепления:
$ z_{2} = z_{s} - z_{1} = 182 - 30 = 152 $ Фактические значения передаточных чисел не должны отличаться от номинальных более чем на: 3% - для одноступенчатых, 4% - для двухступенчатых и 5% - для многоступенчатых редукторов. [1, стр. 22] Отклонение от номинального передаточного числа
$ Δ = \frac{(u - u_{ф})}{u} = \frac{(5-5,07)}{5}= 1,4 % $ КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Коэффициент YA учитывает влияние двустороннего приложения нагрузки (реверса). При одностороннем приложении нагрузки YA = 1. При реверсивном нагружении и одинаковых нагрузке и числе циклов нагружения в прямом и обратном направлении (например, зубья сателлита в планетарной передаче): Y_{A} = 0,65 для нормализованных и улучшенных сталей; Y_{A} = 0,75 для закаленных и цементированных; Y_{A} = 0,9 для азотированных Так как в проектируемой передаче (не)планируется реверсивный ход, то с учетом ТО принимаем: для шестерни (улучшение и закалка ТВЧ)
$ Y_{A_{1}} = 0,75 $ для колеса (улучшение)
$ Y_{A_{2}} = 0,65 $ Для шестерни:
$ [σ]_{F_{1}} = \frac{[σ]_{F_{lim_{1}}}Y_{N_{ш}}Y_{R}Y_{A_{1}}}{S_{F_{1}}} = \frac{600×1×1,1×0,75}{1,7}=291,18 МПа $ Для колеса:
$ [σ]_{F_{2}} = \frac{[σ]_{F_{lim_{2}}}Y_{N_{кол}}Y_{R}Y_{A_{2}}}{S_{F_{2}}} = \frac{431×1×1,1×0,65}{1,7}=181,27 МПа $ Проектный расчет Межосевое расстояние Предварительное значение межосевого расcтояния a'W мм:
$ a'_{W}=K(u±1)(\frac{T_{1}}{u})^{\frac{1}{3}} $ где знак "+" (в скобках) относят к внешнему зацеплению, знак "-" - к внутреннему; T1 - вращающий момент на шестерне (наибольший из длительно действующих), Н×м; u - передаточное число. Коэффициент K в зависимости от поверхностной твердости H1 и H2 зубьев шестерни и колеса соответственно имеет следующие значения [1, стр. 17]: Поверхностная твердость и шестерни до 480 HB и колеса до 262 HB, поэтому принимаем коэффициент
$ K = 8 $
$ U = 5 $
$ a'_{W} = 8(5+1)(\frac{51,43}{5})^{\frac{1}{3}}= 104,39 мм $ Окружную скорость ν, м/с, вычисляют по формуле:
$ ν=\frac{2πa'_{w}n_{1}}{6×10^{4}(u±1)}=\frac{2π×104,39×1445}{6×10^{4}(5±1)}=2,63 м/с $ Степень точности зубчатой передачи назначают по табл. [1, табл. 2.5]: При окружной скорости 2,63 м/с (что меньше 6 м/с) выбираем степень точности 8 - передачи пониженной точности. Уточняем предварительно найденное значение межосевого расстояния:
$ a_{W}=K_{a}(u±1)(\frac{K_{H}T_{1}}{ψ_{ba}u[σ]^{2}_{H}})^{1/3} $ где Ka = 450 - для прямозубых колес; Ka = 410 - для косозубых и шевронных, МПа; [σ]H - в МПа. ψba - коэффициент ширины принимают из ряда стандартных чисел: 0,1; 0,15; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63 в зависимости от положения колес относительно опор: при симметричном расположении 0,315-0,5; при несимметричном 0,25-0,4; при консольном расположении одного или обоих колес 0,25-0,4; Для шевронных передач ψba = 0,4 - 0,63; для коробок передач ψba = 0,1 - 0,2; для передач внутреннего зацепления ψba = 0,2 (u+1)/(u-1). Меньшие значения ψba - для передач с твердостью зубьев H ≥ 45HRC. Принимаем
$ ψ_{ba} = 0,31 $ Коэффициент нагрузки в расчетах на контактную прочность
$ K_{H} = K_{H_{ν}}K_{H_{β}}K_{H_{α}} $ Коэффициент KHν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса. Значения KHν принимают в зависимости от степени точности передачи по нормам плавности, окружной скорости и твердости рабочих поверхностей. Табл. [1, табл. 2.6] Примечание. В числителе приведены значения для прямозубых, в знаменателе - для косозубых зубчатых колёс. Для степени точности 8, максимальной окружной скорости 2,63 м/с, твердости HB≤350 принимаем
$ K_{H_{ν}} = 1,15 $ Коэффициент KHβ учитывает неравномерность распределения нагрузки по длине контактных линий, обусловливаемую погрешностями изготовления (погрешностями направления зуба) и упругими деформациями валов, подшипников. Зубья зубчатых колес могут прирабатываться: в результате повышенного местного изнашивания распределение нагрузки становится более равномерным. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы K0Hβ и после приработки KHβ. Значение коэффициента K0Hβ принимают по таблице 6 в зависимости от коэффициента ψbd = b2/d1, схемы передачи и твердости зубьев. Так как ширина колеса и диаметр шестерни еще не определены, значение коэффициента ψbd вычисляют ориентировочно:
$ ψ_{bd} = 0,5ψ_{ba} (u ± 1) = 0,5 × 0,31 × (5 + 1) = 0,93 $ Коэффициент KHβ определяют по формуле:
$ K_{H_{β}} = 1 + (K^{0}_{H_{β}} - 1)K_{H_{W}} $ где KHw - коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7). Коэффициент KHα определяют по формуле:
$ K_{H_{α}} = 1 + (K^{0}_{H_{α}} - 1)K_{H_{W}} $ где KHw - коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7). Начальное значение коэффициента K0Hα распределения нагрузки между зубьямив связи с погрешностями изготовления (погрешностями шага зацепления и направления зуба) определяют в зависимости от степени точности (nст = 5, 6, 7, 8, 9) по нормам плавности: для прямозубых передач K^{0}_{H_{α}} = 1 + 0,06(n_{ст} - 5), при условии 1 ≤ K^{0}_{H_{α}} ≤ 1,25; K^{0}_{H_{α}} = 1 + A(n_{ст} - 5), при условии 1 ≤ K^{0}_{H_{α}} ≤ 1,6, для косозубых передач где A = 0,15 - для зубчатых колес с твердостью H1 и H2 > 350 HB и A = 0,25 при H1 и H2 ≤ 350 HB или H1 > 350 HB и H2 ≤ 350 HB
$ K^{0}_{H_{α}} = 1 + 0,06(9 - 5) = 1,24 $ Принимаем коэффициент KHw по табл. 7 равным (ближайшее значение твердости по таблице 250 HB или 23 HRC к твердости колеса 262 HB) 0,28
$ K_{H_{α}} = 1 + (1,24 - 1)0,28 = 1,0672 $ Принимаем коэффициент K0Hβ по табл. 6 (схема 3) равным 1,02
$ K_{H_{β}} = 1 + (1,02 - 1) 0,28 = 1,0056 $
$ K_{H} = 1,12 × 1,0056 × 1,0672 = 1,2020 $ Уточнённое значение меж осевого расстояния:
$ a_{W} =450(5±1)(\frac{1,2020×51,43}{0,31×5×(482,82)^{2}})^{\frac{1}{3}}= $
$ = 151,21 мм $ КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Коэффициент ZV учитывающий влияние окружной скорости V, принимаем как для шестерни так и для колеса и удовлетворяющий в большинстве случаев
$ Z_{V}=1,05 $ Для шестерни:
$ [σ]_{H_{1}} = \frac{[σ]_{H_{lim}}Z_{N_{ш}}Z_{R}Z_{V}}{S_{H}}=\frac{1016×1×0,9×1,05}{1,2}=800,1 МПа $ Для колеса:
$ [σ]_{H_{2}} = \frac{[σ]_{H_{lim}}Z_{N_{кол}}Z_{R}Z_{V}}{S_{H}}=\frac{562×1×0,9×1,05}{1,1}=482,8 МПа $ Допускаемое напряжение [σ]H для цилиндрических и конических передач с прямыми зубьями равно меньшему из допускаемых напряжений шестерни [σ]H1 и колеса [σ]H2
$ [σ]_{H} = 482,8 МПа $ Определение напряжений изгиба Допускаемые напряжения изгиба зубьев шестерни [σ]F1 и колеса [σ]F2 определяют по общей зависимости (но с подстановкой соответствующих параметров для шестерни и колеса), учитывая влияние на сопротивление усталости при изгибе долговечности (ресурса), шероховатости поверхности выкружки (переходной поверхности между смежными зубьями) и реверса (двустороннего приложения) нагрузки: Предел прочности [σ]Flim при отнулевом цикле напряжений вычисляют по эмпирическим формулам. 1. табл. 2.3
$ [σ]_{F} =\frac{[σ]_{F_{lim}}Y_{N}Y_{R}Y_{A}}{S_{F}} $ Принимаем для выбранной марки стали и ТО (Сталь 40Х, улучшение и закалка ТВЧ) шестерни
$ [σ]_{F_{lim 1}} = 600 МПа $ Для колеса (Сталь 40Х, улучшение)
$ [σ]_{F_{lim 2}} = 1,75 HB_{ср} = 1,75 × 246 = 431 МПа $ Минимальное значение коэффициента запаса прочности: для цементированных и нитроцементированных зубчатых колес - SF = 1,55; для остальных - SF = 1,7. Принимаем для шестерни (улучшение и закалка ТВЧ)
$ S_{F_{1} = 1,7 $ Для колеса (улучшение)
$ S_{F_{2}} = 1,7 $ Коэффициент долговечности YN учитывает влияние ресурса:
$ Y_{N} = (\frac{N_{F_{lim}}}{N_{k}})^{(\frac{1}{q})}, при условии 1≤Y_{N}≤Y_{N_{max}} $ Для закаленных и поверхностно упрочненных зубьев
$ Y_{N_{max}} = 2,5 и q = 9 $ Число циклов, соответствующее перегибу кривой усталости
$ N_{F_{lim}} = 4 × 10^{6} $ Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем
$ Y_{N_{max 1}} = 2,5 и q_{1} = 9 $ Для выбранной ТО колеса (улучшение) принимаем
$ Y_{N_{max 2}} = 2,5 и q_{2} = 9 $ Назначенный ресурс Nk вычисляют так же, как и при расчетах по контактным напряжениям. В соотеветствии с кривой усталости напряжения σF не могут иметь значений меньших σFlim. Поэтому при Nk > NFlim принимают Nk = NFlim. Для длительно работающих быстроходных передач Nk ≥ NFlim и, следовательно YN = 1, что и учитывает первый знак неравенства в (2). Второй знак неравенства ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба. Для шестерни:
$ N_{k}=60nn_{з}L_{h}=60×1445×1×33533,28=2907335376 $
$ Y_{N_{ш}} = 1 $ Т.к. Nk ш > NFG, то принимаем
$ N_{k ш} = N_{FG} = 4000000 $ Для колеса:
$ N_{k кол} = 60 × 291 × 1 × 33533.28 = 585489672 $
$ Y_{N кол} = 1 $ Т.к. Nk кол > NFG, то принимаем
$ N_{k кол} = N_{FG} = 4000000 $ Коэффициент YR, учитывающий влияние шероховатости переходной поверхности между зубьями, принимают: YR = 1 при шлифовании и зубофрезеровании с параметром шероховатости RZ ≤ 40 мкм; YR = 1,05...1,2 при полировании (большие значения при улучшении и после закалки ТВЧ). Принимаем
$ Y_{R} = 1,1 $ КомментарииРасчет зубчатых колес цилиндрической передачи первой ступени
Спроектировать привод цепного конвейера. Расчет зубчатых колес редуктора двухступенчатого цилиндрического с разветвленной выходной ступенью 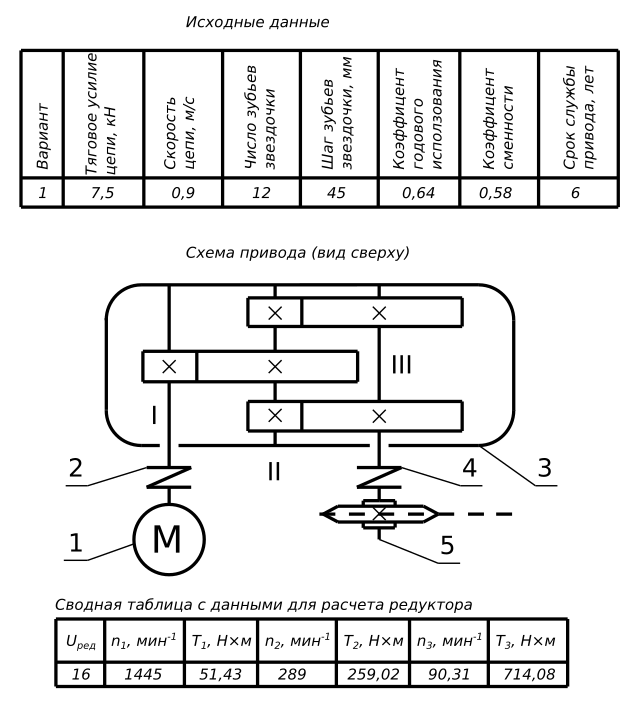
Расчет зубчатых колес В зависимости от вида изделия, условий его эксплуатации и требований к габаритным размерам выбирают необходимую твердость колес и материалы для их изготовления. Для силовых передач чаще всего применяют стали. Передачи со стальными зубчатыми колесами имеют минимальную массу и габариты, тем меньше, чем выше твердость рабочих поверхностей зубьев, которая в свою очередь зависит от марки стали и варианта термической обработки. 1. табл. 2.1 Цилиндрическая передача первой ступени. Шестерня. Материал - Сталь 40Х. Назначаем термическую обработку - улучшение и закалка ТВЧ. Предельные размеры заготовки: Dпр = 125 мм, Sпр = 80 мм. Твердость зубьев: в сердцевине до 302 HB, на поверхности до 50 HRCэ. Предельное напряжение
$ σ_{T} = 750 МПа $ Колесо. Материал - Сталь 40Х. Назначаем термическую обработку - улучшение. Предельные размеры заготовки: Dпр = 200 мм, Sпр = 125 мм. Твердость зубьев: в сердцевине до 262 HB, на поверхности до 262 HB. Предельное напряжение
$ σ_{T} = 640 МПа $ Определяем допускаемые контактные напряжения
$ [σ]_{H} = \frac{[σ]_{H_{lim}}Z_{N}Z_{R}Z_{V}}{S_{H}} $ Предел контактной выносливости [σ]Hlim вычисляют по эмпирическим формулам в зависимости от материала и способа термической обработки зубчатого колеса и средней твердости (HBср или HRCэ ср) на поверхности зубьев (табл. 2.2). Для выбранной марки стали и ТО шестерни:
$ [σ]_{H_{lim_{1}}}=17×HRC_{э ср} + 200 = 17 × 48 + 200 = 1016 МПа $ Для выбранной марки стали и ТО колеса:
$ [σ]_{H_{lim_{2}}} = 2 × HB_{ср} + 70 = 2 × 246 + 70 = 562 МПа $ Минимальные значения коэффициента запаса прочности для зубчатых колес с однородной структурой материала (улучшенных, объемно закаленных) SH = 1,1; для зубчатых колес с поверхностным упрочнением SH = 1,2. Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем
$ S_{H_{1}} = 1,2 $ Для выбранной ТО колеса (улучшение) принимаем
$ S_{H_{2}} = 1,1 $ Коэффициент долговечности ZN учитывает влияние ресурса
$ Z_{N}=(\frac{N_{HG}}{N_{k}})^{\frac{1}{6}} при условии 1 ≤ Z_{N} ≤р Z_{N_{max}} $ Число NHG циклов, соответсвующее перелому кривой усталости, определяют по средней твердости поверхностей зубьев [1, стр. 13]:
$ N_{HG}=30HB^{2,4}_{ср} ≤ 12×10^{7} $ Твердость в единицах HRC переводят в единицы HB: Переведенная средняя твердость поверхности зубьев для выбранного материала шестерни равна 451 HB. Для шестерни
$ N_{HG_{1}} = 30×451^{2,4} = 70405590 $ Для колеса
$ N_{HG_{2}} = 30×246^{2,4} = 16464600 $ Ресурс Nk передачи в числах циклов перемены напряжений при частоте вращения n, мин-1, и времени работы Lh, час:
$ N_{k} = 60nn_{з}L_{h} $ где nз - число вхождений в зацепление зуба рассчитываемого колеса за один его оборот (численно равно числу колес, находящихся в зацеплении с рассчитываемым). Число зацеплений nз и для колеса и для шестерни в данном случае
$ n_{з} = 1 $ В общем случае суммарное время Lh (в ч) работы передачи вычисляют по формуле:
$ L_{h} = L365K_{год}24K_{сут}=6×365×0,64×24×0,58 = 19510 ч $ Где L - число лет работы; Kгод - коэффициент годового использования передачи; Kсут - коэффициент суточного использования передачи. Для шестерни:
$ N_{k_{ш}} = 60 × 1445 × 1 × 19510 = 1691517000 $ Т.к. Nk ш > NHG, то принимаем
$ N{k_{ш}} = N_{HG} = 70405590 $
$ Z_{N_{ш}} = 1 $ Для колеса:
$ N_{k_{кол}} = 60 × 291 × 1 × 19510 = 340644600 $ Т.к. Nk кол > NHG, то принимаем
$ N_{k_{кол}} = N_{HG} = 16464600 $
$ Z_{N_{к}} = 1 $ Коэффициент ZR, учитывающий влияние шероховатости сопряженных поверхностей зубьев, для шестерни и колеса принимаем
$ Z_{R}= 0,9 $ КомментарииКинематический расчет привода
Кинематический расчет привода цепного конвейера 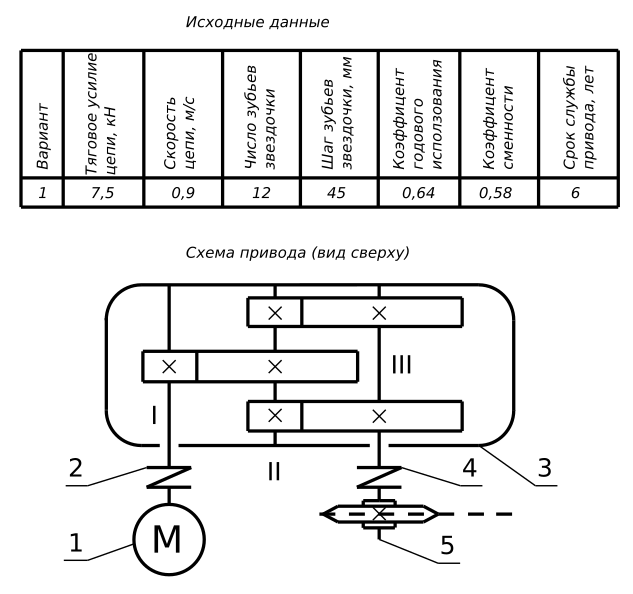
Кинематический расчет привода Скорость цепи
$ υ_{ц} = \frac{ω_{зв}d}{2} $ Угловая скорость вращения ведомого вала редуктора
$ ω_{зв} = \frac{2υ_{ц}}{d} = \frac{2×0,9×1000}{174} = 10,35 с^{-1} $ В то же время
$ ω_{зв} = \frac{2πn_{зв}}{60} = \frac{πn_{зв}}{30} $ Частота вращения выходного (ведомого) вала редуктора
$ n_{зв} = \frac{30ω_{зв}}{π} = \frac{30×10,35}{π} = 98,84 мин^{-1} $ Передаточное число редуктора
$ u_{р} = \frac{n_{1}}{n_{зв}} = \frac{1455}{98,84} = 14,72 $ Назначаем по ГОСТ 21426-75 ближайшую величину. 1. таблица 1.4
$ u_{р} = 16 $ Тогда
$ n_{зв} = \frac{n_{1}}{u_{р}} = \frac{1455}{16} = 90,94 мин^{-1} $ Полученное расчетом общее передаточное число распределяют между отдельными ступенями редуктора. 1. таблица 1.4 Передаточное число тихоходной ступени
$ U_{Т} = 0,88\sqrt{Uред} = 0,88\sqrt{16}= 3,2 $ Передаточное число быстроходной ступени
$ U_{Б} = \frac{U_{ред}}{U_{Т}} = \frac{16}{3,2} = 5 $ Частота вращения вала выходного (ведомого):
$ n_{3} = n_{зв} = n_{в} = 90,94 мин^{-1} $ Частота вращения вала промежуточного:
$ n_{2} = n_{3}U_{Т} = 90,94×3,2 = 291 мин^{-1} $ Частота вращения вала входного (ведущего):
$ n_{1} = n_{2}U_{Б} = 291×5 = 1455 мин^{-1} $ Угловые скорости валов:
$ ω_{i} = \frac{πn_{i}}{30} $ Входного (ведущего):
$ ω_{1} = \frac{πn_{1}}{30} = \frac{π1455}{30} = 152,37 с^{-1} $ Промежуточного:
$ ω_{2} = \frac{πn_{2}}{30} = \frac{π291}{30} = 30,47 с^{-1} $ Выходного (ведомого):
$ ω_{3} = \frac{πn_{3}}{30} = \frac{π90,94}{30} = 9,52 с^{-1} $ Крутящие моменты на валах редуктора: На выходном (ведомом)
$ T_{3}=\frac{10^{3}P_{3}}{ω_{3}}=\frac{10^{3}×7,5}{9,52}=787,82 Н×м; $ На промежуточном
$ T_{2}=\frac{T_{3}}{(U_{Т}η_{з.п}η^{2}_{п.к})}=\frac{787,82}{(3,2×0,97×0,992)}=259,02 Н×м; $ На входном (ведущем)
$ T_{1}=\frac{T_{2}}{(U_{Б}η_{з.п}η^{2}_{п.к})}=\frac{259}{(5×0,97×0,992)}=54,49 Н×м $ Полученные значения сводим в таблицу 
Кинематический расчет привода Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил. КомментарииРасчет требуемой мощности электродвигателя
Расчет требуемой мощности и выбор электродвигателя Для выбора электродвигателя определяем требуемую от него мощность и частоту вращения 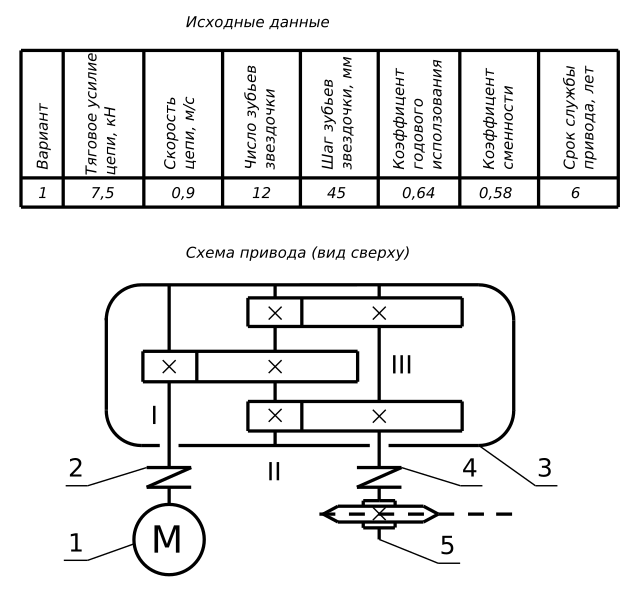
Расчет требуемой мощности электродвигателя Диаметр делительной окружности звездочки
$ d = \frac{t}{sin(\frac{π}{z})} = \frac{45}{sin(\frac{π}{12})} = 174 мм $ Шаг цепи звездочки
$ t = 45 мм $ Находим мощность (кВт) привода (мощность на выходе)
$ P_{в} = \frac{Fυ}{10^{3}} = \frac{7500 × 0,9}{1000} = 6,75 кВт $ Тогда требуемая мощность электродвигателя
$ P_{э.тр} = \frac{P_{в}}{η_{общ}} = \frac{6,75}{0,90} = 7,52 кВт $ Величину ηобщ определяют в зависимости от КПД (η) звеньев кинематической цепи привода от вала электродвигателя до приводного вала машины
$ η_{общ} = η_{м}×η^{i}_{з.п}×η^{k}_{п.к} = 0,98×0,97^{2}×0,99^{3} = 0,90 $ КПД муфты быстроходного вала. 1. таблица 1.1
$ η_{м} = 0,98 $ КПД одной зубчатой пары (закрытой). 1. таблица 1.1
$ η_{з.п} = 0,97 $ КПД одной пары подшипников качения. 1. таблица 1.1
$ η_{п.к} = 0,99 $ Для двухступенчатого редуктора:
$ i=2 $
$ k=3 $ Для двухступенчатого редуктора: С учетом возможности для двухступенчатого редуктора (u=12,5÷31,5), выбираю электродвигатель типа 4AM132S4Y3, имеющий мощность P1=7,5 кВт при частоте вращения n1=1455 мин-1. 1. таблица 24.9 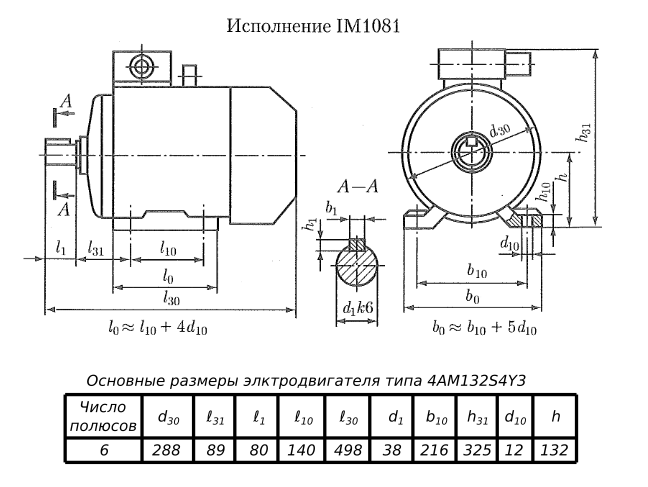
Расчет требуемой мощности электродвигателя Список используемой литературы: 1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов., 2008. - 492 с., ил. КомментарииРасчет зубчатых колес цилиндрической передачи второй ступени
Спроектировать привод цепного конвейера. Расчет зубчатых колес редуктора двухступенчатого цилиндрического с разветвленной выходной ступенью 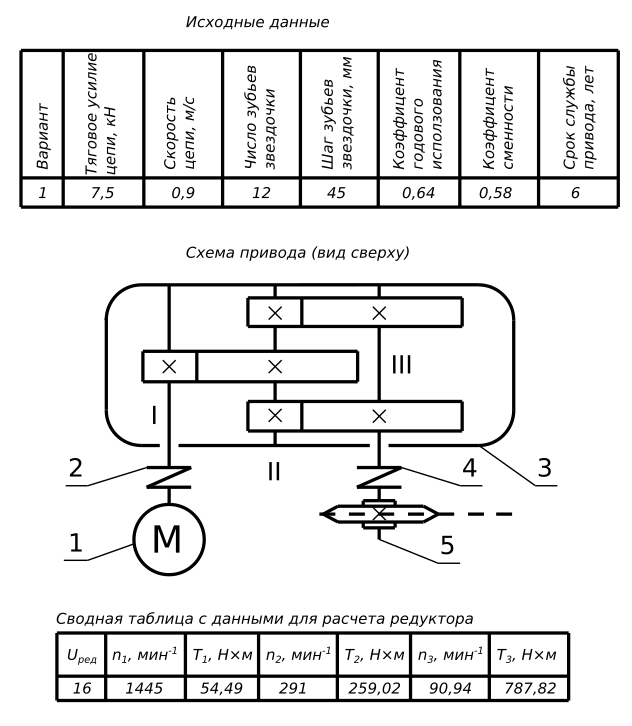
Расчет зубчатых колес В зависимости от вида изделия, условий его эксплуатации и требований к габаритным размерам выбирают необходимую твердость колес и материалы для их изготовления. Для силовых передач чаще всего применяют стали. Передачи со стальными зубчатыми колесами имеют минимальную массу и габариты, тем меньше, чем выше твердость рабочих поверхностей зубьев, которая в свою очередь зависит от марки стали и варианта термической обработки. 1. табл. 2.1 Цилиндрическая передача второй ступени Шестерня. Материал - Сталь 40Х. Назначаем термическую обработку - улучшение и закалка ТВЧ. Предельные размеры заготовки: Dпр = 125 мм, Sпр = 80 мм. Твердость зубьев: в сердцевине до 302 HB, на поверхности до 50 HRCэ. Предельное напряжение
$ σ_{T} = 750 МПа $ Колесо. Материал - Сталь 40Х. Назначаем термическую обработку - улучшение. Предельные размеры заготовки: Dпр = 200 мм, Sпр = 125 мм. Твердость зубьев: в сердцевине до 262 HB, на поверхности до 262 HB. Предельное напряжение
$ σ_{T} = 640 МПа $ Определяем допускаемые контактные напряжения
$ [σ]_{H} = \frac{[σ]_{H_{lim}}Z_{N}Z_{R}Z_{V}}{S_{H}} $ Предел контактной выносливости [σ]Hlim вычисляют по эмпирическим фомулам в зависимости от материала и способа термической обработки зубчатого колеса и средней твердости (HBср или HRCэ ср) на поверхности зубьев (табл. 2.2). Для выбранной марки стали и ТО шестерни:
$ [σ]_{H_{lim_{1}}}=17×HRC_{э ср} + 200 = 17 × 48 + 200 = 1016 МПа $ Для выбранной марки стали и ТО колеса:
$ [σ]_{H_{lim_{2}}} = 2 × HB_{ср} + 70 = 2 × 246 + 70 = 562 МПа $ Минимальные значения коэффициента запаса прочности для зубчатых колес с однородной структурой материала (улучшенных, объемно закаленных) SH = 1,1; для зубчатых колес с поверхностным упрочнением SH = 1,2. Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем
$ S_{H_{1}} = 1,2 $ Для выбранной ТО колеса (улучшение) принимаем
$ S_{H_{2}} = 1,1 $ Коэффициент долговечности ZN учитывает влияние ресурса
$ Z_{N}=(\frac{N_{HG}}{N_{k}})^{\frac{1}{6}} при условии 1 ≤ Z_{N} ≤р Z_{N_{max}} $ Число NHG циклов, соответсвующее перелому кривой усталости, определяют по средней твердости поверхностей зубьев [1, стр. 13]:
$ N_{HG}=30HB^{2,4}_{ср} ≤ 12×10^{7} $ Твердость в единицах HRC переводят в единицы HB: Переведенная средняя твердость поверхности зубьев для выбранного материала шестерни равна 451 HB. Для шестерни
$ N_{HG_{1}} = 30×451^{2,4} = 70405590 $ Для колеса
$ N_{HG_{2}} = 30×246^{2,4} = 16464600 $ Ресурс Nk передачи в числах циклов перемены напряжений при частоте вращения n, мин-1, и времени работы Lh, час:
$ N_{k} = 60nn_{з}L_{h} $ где nз - число вхождений в зацепление зуба рассчитываемого колеса за один его оборот (численно равно числу колес, находящихся в зацеплении с рассчитываемым). Число зацеплений nз и для колеса и для шестерни в данном случае
$ n_{з} = 1 $ В общем случае суммарное время Lh (в ч) работы передачи вычисляют по формуле:
$ L_{h} = L365K_{год}24K_{сут}=6×365×0,64×24×0,58 = 19510 ч $ Где L - число лет работы; Kгод - коэффициент годового использования передачи; Kсут - коэффициент суточного использования передачи. Для шестерни:
$ N_{k_{ш}} = 60 × 291 × 1 × 19510 = 1691540582 $ Т.к. Nk ш > NHG, то принимаем
$ N_{k_{ш}} = N_{HG} = 70405590 $
$ Z_{N_{ш}} = 1 $ Для колеса:
$ N_{k_{кол}} = 60 × 91 × 1 × 19510 = 105721286 $ Т.к. Nk кол > NHG, то принимаем
$ N_{k_{кол}} = N_{HG} = 16464600 $
$ Z_{N_{к}} = 1 $ Коэффициент ZR, учитывающий влияние шероховатости сопряженных поверхностей зубьев, для шестерни и колеса принимаем
$ Z_{R}= 0,9 $ Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |


Комментарии