Все решения инженера @NICKпостроить проекции и натуральный вид сечения тела плоскостью построить развертку усеченной части тела
Построить проекции и натуральный вид сечения тела плоскостью построить развертку усеченной части тела 
Построить проекции и натуральный вид сечения тела плоскостью построить развертку усеченной части тела Построить проекции и натуральный вид сечения поверхности пирамиды плоскостью
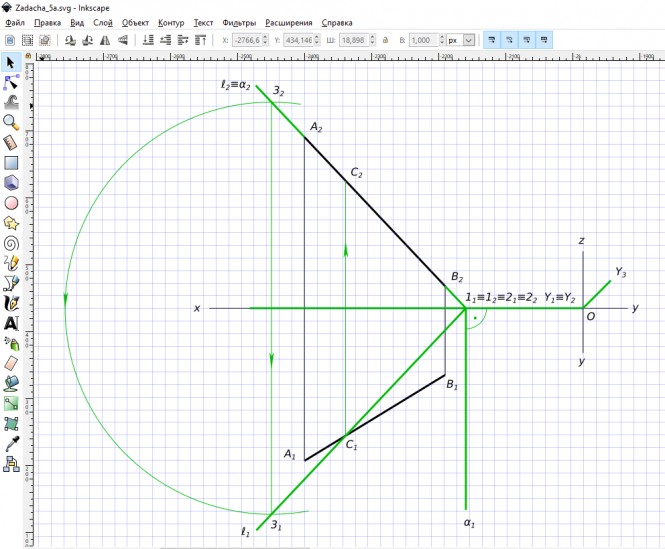
1. Построить проекции и натуральный вид сечения поверхности пирамиды плоскостью. 2. Определить натуральную величину расстояния от (.)«S» до прямой «m». 3. Определить натуральную величину угла между ребром пирамиды и основанием. КомментарииНа прямой l найти точку равноудаленную от точек A и B
На прямой l найти точку равноудаленную от точек A и B 
На прямой l найти точку равноудаленную от точек A и B КомментарииПостроить проекции ромба. если ac || π2 – диагональ ромба abcd, вершина b принадлежит π1, вершина d равноудалена ...
Построить проекции ромба, если ac || π2 – диагональ ромба abcd, вершина b принадлежит π1, вершина d равноудалена от плоскостей проекций π1 и π2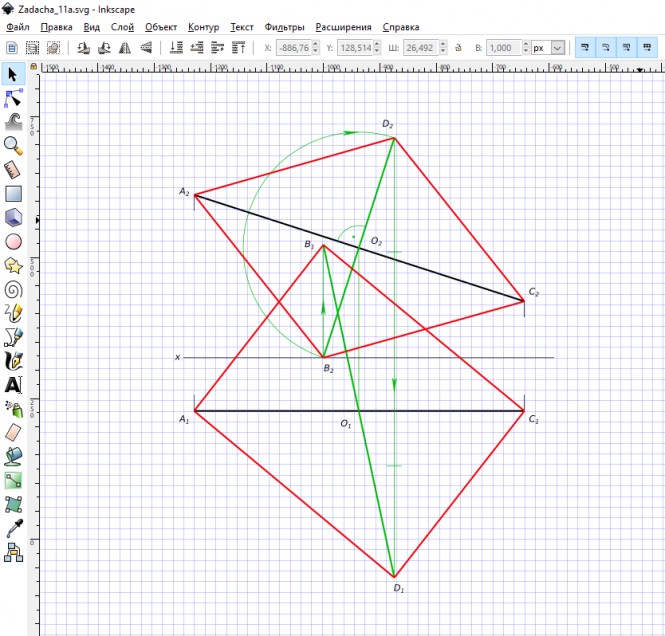 
Построить проекции ромба, если ac || π2 – диагональ ромба abcd, вершина b принадлежит π1, вершина d равноудалена от плоскостей проекций π1 и π2 КомментарииПостроить равнобедренный треугольник
Построить равнобедренный треугольник ABC с основанием BC на прямой MN. Для треугольника должно выполняться условие AC = 1,25h (h – высота треугольника). 
Построить равнобедренный треугольник Построить проекции равностороннего треугольника ABC со стороной BC на прямой mn: A(65,75,80) M(10,25,0) N(160,25,50)
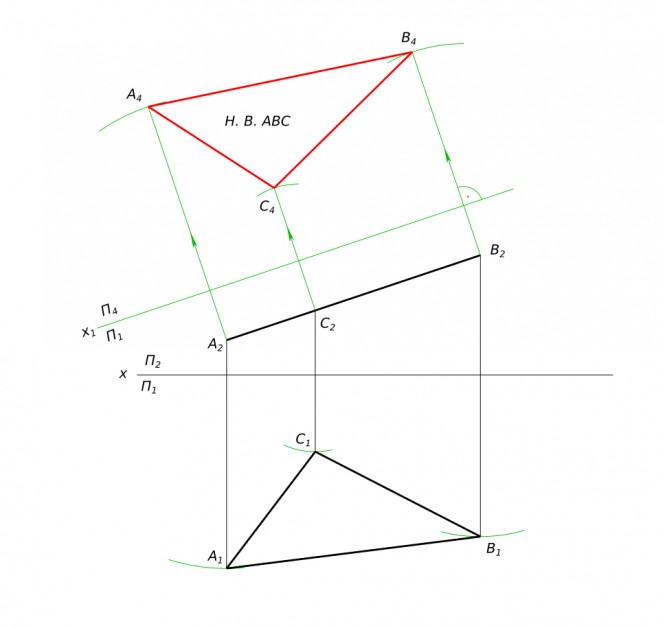
Построить проекции равностороннего треугольника ABC со стороной BC на прямой mn: A(65,75,80) M(10,25,0) N(160,25,50). Построить истинный вид треугольника.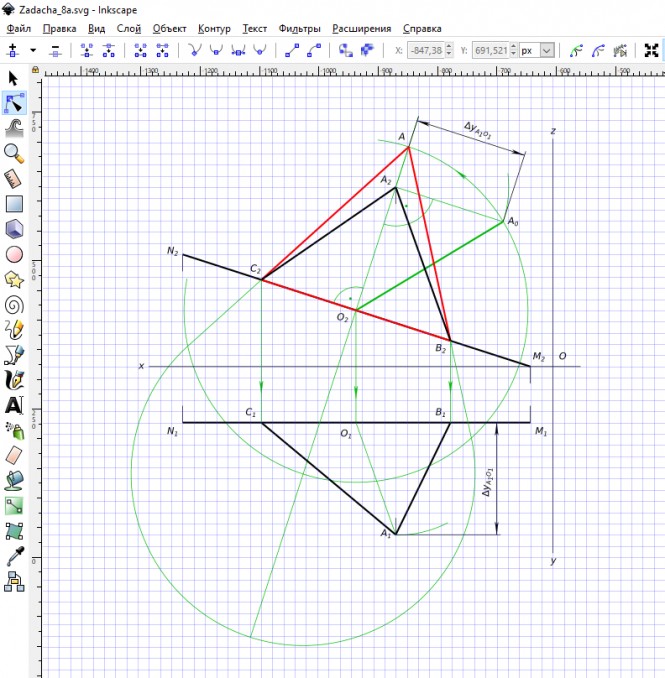 
Построить проекции равностороннего треугольника ABC со стороной BC на прямой mn: A(65,75,80) M(10,25,0) N(160,25,50) КомментарииОпределить расстояние от точки A до прямой BC. Задачу решить методом вращения вокруг проецирующей прямой.
Определить расстояние от точки A до прямой BC. Задачу решить методом вращения вокруг проецирующей прямой.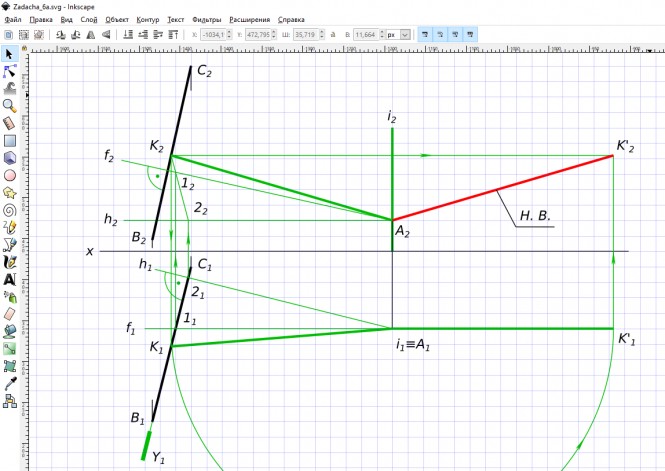 
Определить расстояние от точки A до прямой BC. Задачу решить методом вращения вокруг проецирующей прямой. КомментарииНайти точку на прямой, равноудаленную от плоскостей проекций П1 и П2
Найти точку на прямой, равноудаленную от плоскостей проекций П1 и П2 
Найти точку на прямой, равноудаленную от плоскостей проекций П1 и П2 КомментарииОпределить натуральную величину двугранного угла при ребре AC
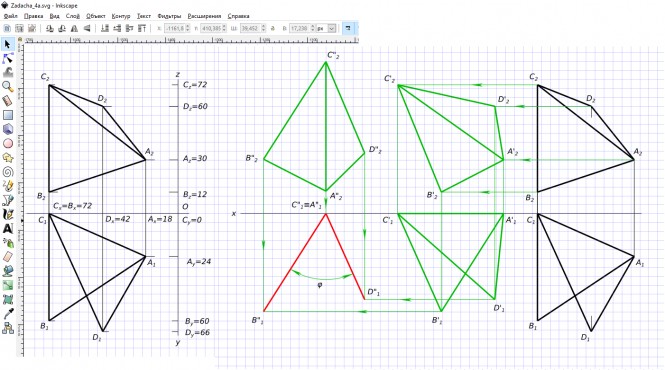
Построить две проекции треугольников ABC и ACD по заданным координатам и определить натуральную величину двугранного угла при ребре AC. A(х18, у24,z30), B(x72, y60, z12), C(z72, y0, z72), D (x42, y66, z60). 
Определить натуральную величину двугранного угла при ребре AC Комментариипроверка почты
Через точку A провести горизонталь и фронталь пересекающие профильную прямую
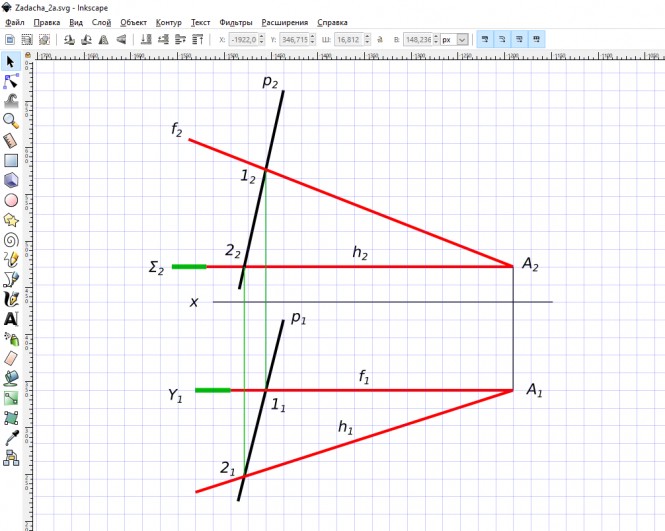
Через точку A провести горизонталь и фронталь пересекающие профильную прямую 
Через точку A провести горизонталь и фронталь пересекающие профильную прямую КомментарииЧерез точку A провести горизонталь и фронталь пересекающие прямую p
Через точку A провести горизонталь и фронталь пересекающие прямую p 
Через точку A провести горизонталь и фронталь пересекающие прямую p КомментарииПо заданным координатам построить фронтальную и горизонтальную проекции треугольника ABC. В плоскости треугольника провести ...
По заданным координатам (табл. 1) построить фронтальную и горизонтальную проекции треугольника ABC. В плоскости треугольника провести произвольные горизонталь и фронталь. Определение прямых и проведение прямых частного положения смотрим в курсе NGEO (три точки в меню). таблица 1
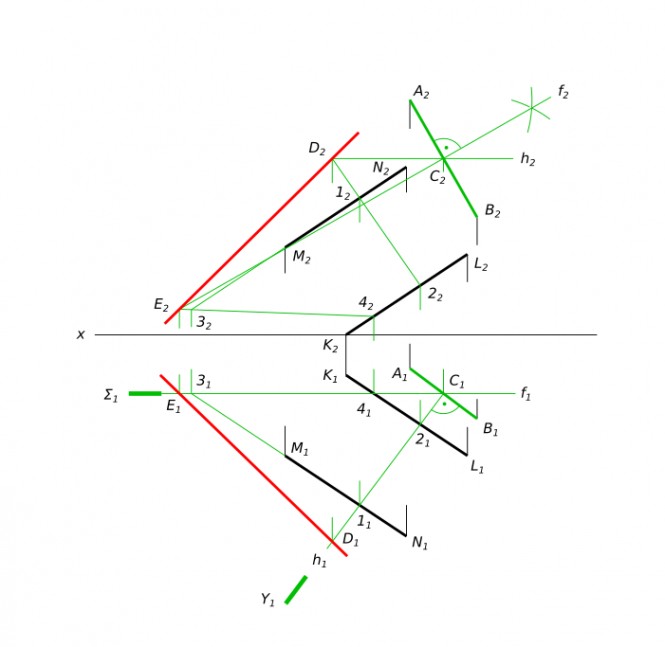
По заданным координатам (табл. 1) построить фронтальную и горизонтальную проекции треугольника ABC. В плоскости треугольника провести произвольные горизонталь и фронталь КомментарииВ плоскости α(MN параллельна LK) построить множество точек равноудаленных от двух данных A и B
В плоскости α(MN параллельна LK) построить множество точек равноудаленных от двух данных A и B, если A(35,10,70, B(15,25,35), M(72,36,26), N(36, 60, 50), K(54, 12, 0). 
В плоскости α(MN параллельна LK) построить множество точек равноудаленных от двух данных A и B КомментарииКран сливной сборочный чертеж. Надо сделать чертежи деталей: 2,3,4 позиции. По отдельности на каждом листе по два изображения. Как это делать?
Кран сливной сборочный чертеж. Надо сделать чертежи деталей: 2,3,4 позиции. По отдельности на каждом листе по два изображения 
Кран сливной сборочный чертеж. Надо сделать чертежи деталей: 2,3,4 позиции. По отдельности на каждом листе по два изображения Как это делать? Да, очень просто! Получите изображение сборочного чертежа во весь экран, например, в программе просмотра фотографий. Затем рассчитайте масштаб полученного изображения: размер 205, указанный на чертеже, разделите на тот же размер измеренный с помощью линейки. Далее размеры деталей получаем измеряя их с помощью линейки и умножения на масштаб. КомментарииНужно выполнить построение вида сбоку и диметрии
Нужно выполнить построение вида сбоку и диметрии КомментарииПостроить линию взаимного пересечения пов-стей установить видимость этих поверхностей. Построить развёртку одной из пов-стей
Построить развёртку одной из поверхностей 
Построить развёртку одной из поверхностей Вид сверху показывать не нужно. КомментарииПостроить линию взаимного пересечения пов-стей установить видимость этих поверхностей. Построить развёртку одной из пов-стей
Построить линию взаимного пересечения поверхностей, установить видимость этих поверхностей. 
Построить линию взаимного пересечения поверхностей, установить видимость этих поверхностей. КомментарииА вторая половина?
Построить линию пересечения поверхности плоскостями и построить натуральную величину сечения
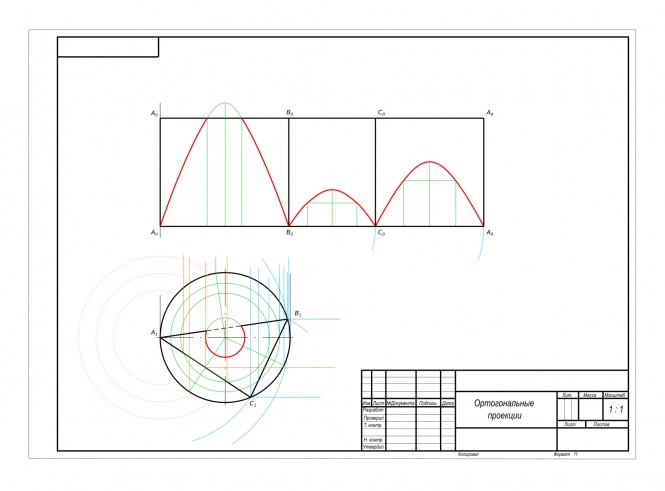
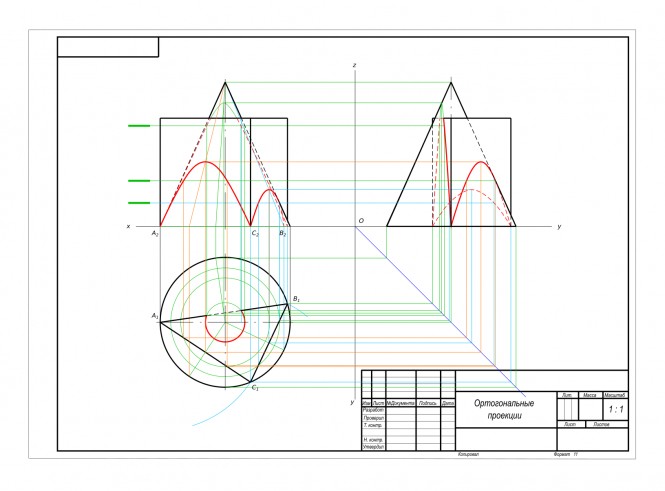
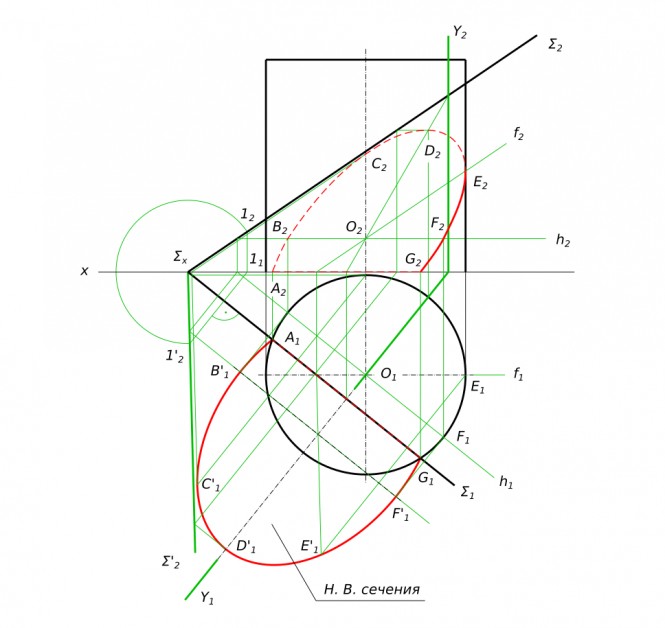
Построить линию пересечения поверхности плоскостями и построить натуральную величину сечения 
Построить линию пересечения поверхности плоскостями и построить натуральную величину сечения КомментарииПо аксонометрическому изображению выполнить чертеж сварного изделия как сборочный чертеж, сделать разрезы, проставить размеры
По аксонометрическому изображению выполнить чертеж сварного изделия как сборочный чертеж, сделать разрезы, проставить размеры, обозначить сварные швы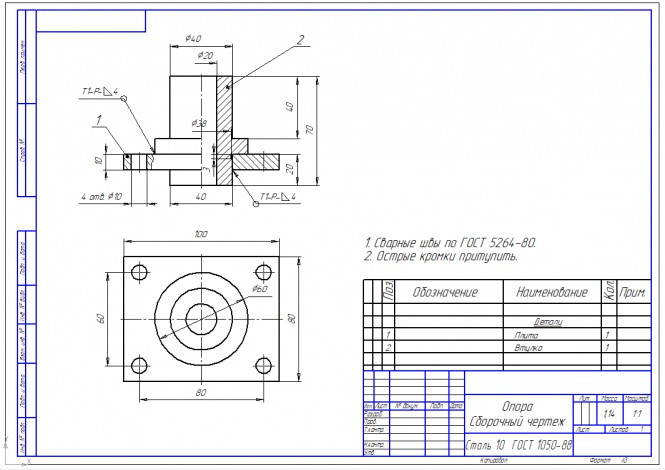 
По аксонометрическому изображению выполнить чертеж сварного изделия как сборочный чертеж, сделать разрезы, проставить размеры, обозначить сварные швы Комментариипо двум видам детали построить третий выполнить разрезы
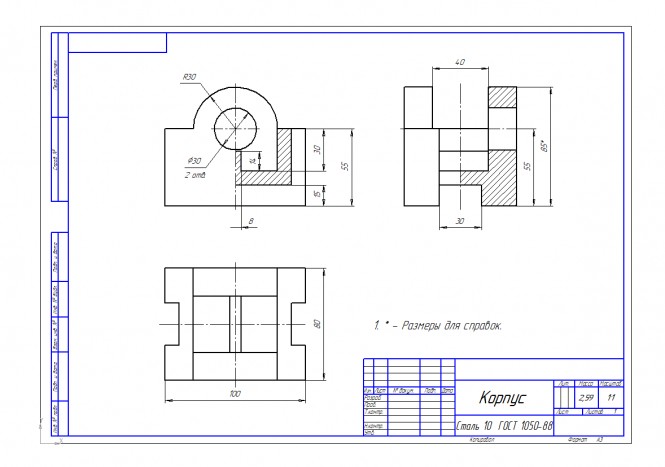
По двум видам детали построить третий. Выполнить разрезы. Проставить размеры 
По двум видам детали построить третий. Выполнить разрезы. Проставить размеры Комментариипо двум видам детали построить третий выполнить разрезы
По двум видам детали построить третий. Выполнить разрезы. Проставить размеры 
По двум видам детали построить третий. Выполнить разрезы. Проставить размеры КомментарииПоследовательность сборки шестеренчатого насоса
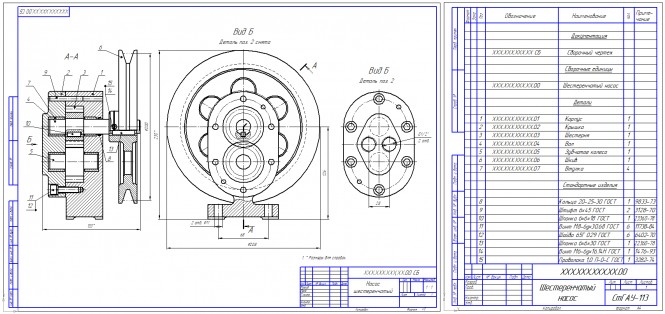
Описать последовательность сборки шестеренчатого насоса изображенного на чертеже в процессе его изготовления 
Последовательность сборки шестеренчатого насоса Сборка шестеренчатого насоса в процессе его изготовления. В корпус (дет. поз. 1) запресовываем (дет. поз. 7) втулки подшипников скольжения , устанавливаем (дет. поз. 8) кольцо уплотнительное. В крышку (дет. поз. 2) запресовывем (дет. поз. 7) втулки подшипников скольжения В вал (дет. поз. 4) запресовываем шпонку (дет. поз. 10) и соединяем его с шестерней (дет. поз. 3). Устанавливаем вал в корпус. Устанавливаем зубчатое колесо (дет. поз. 5) в корпус насоса, вводя его в зацепление с шестерней. Закрываем насос крышкой и устанавливаем крепежные винты, добившись при этом свободного вращения вала, сверлим отверстия под установочные штифты. Вывинчиваем крепежные винты снимаем крышку. Запресовываем установочные штифты в корпус насоса. Закрываем насос крышкой по установочным штифтам. Вращения вала должно остаться свободным. Запресовываем в вал шпонку (дет. поз. 13). На вал устанавливаем шкив (дет. поз. 6), фиксируем его установочным винтом 14 и предупреждаем его вывинчивание проволокой 15. КомментарииПерспектива и тени портала
Перспектива и тени портала 
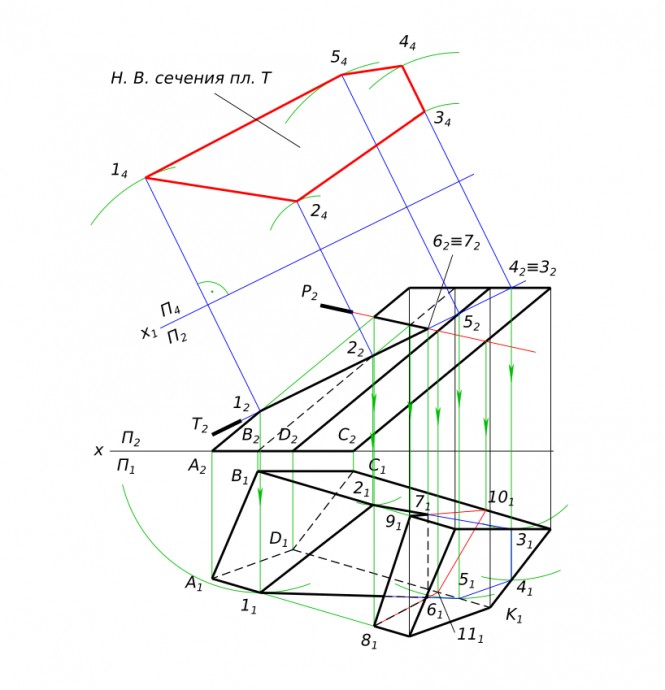
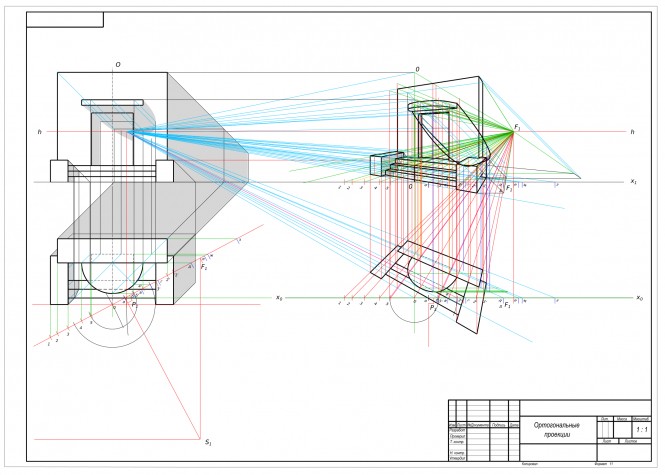
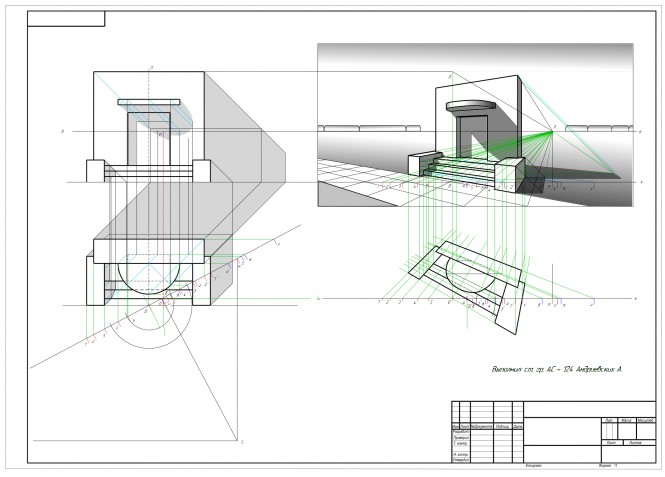
Перспектива и тени портала На картинке ход построения КомментарииПерспектива и тени портала
Перспектива и тени портала 
Перспектива и тени портала КомментарииПостроить проекции и истинную величину сечения тела плоскостью
Построить проекции и истинную величину сечения тела плоскостью 
Построить проекции и истинную величину сечения тела плоскостью КомментарииНайти натуральную величину треугольника лишь одной заменой плоскостей проекций
Найти натуральную величину треугольника лишь одной заменой плоскостей проекций 
Найти натуральную величину треугольника лишь одной заменой плоскостей проекций КомментарииСтальной ступенчатый брус заданной конфигурации подвергается воздействию внешней нагрузки q , P . Построить эпюру продольных сил
Условия задачи. Стальной ступенчатый брус заданной конфигурации подвергается воздействию внешней нагрузки q , P . Требуется: 1. Построить эпюру продольных сил N . 2. Построить эпюру нормальных напряжений при неизвестном значении площади F . 3. Записать условие прочности и определить необходимое значение F при допускаемом напряжении 160 МПа. Затем назначить площадь поперечного сечения Fi на каждом участке бруса, соблюдая указанные на схеме соотношения между F и Fi . 4. Построить эпюру продольных перемещений u , принимая модуль упругости E= 2 *10^5 МПа.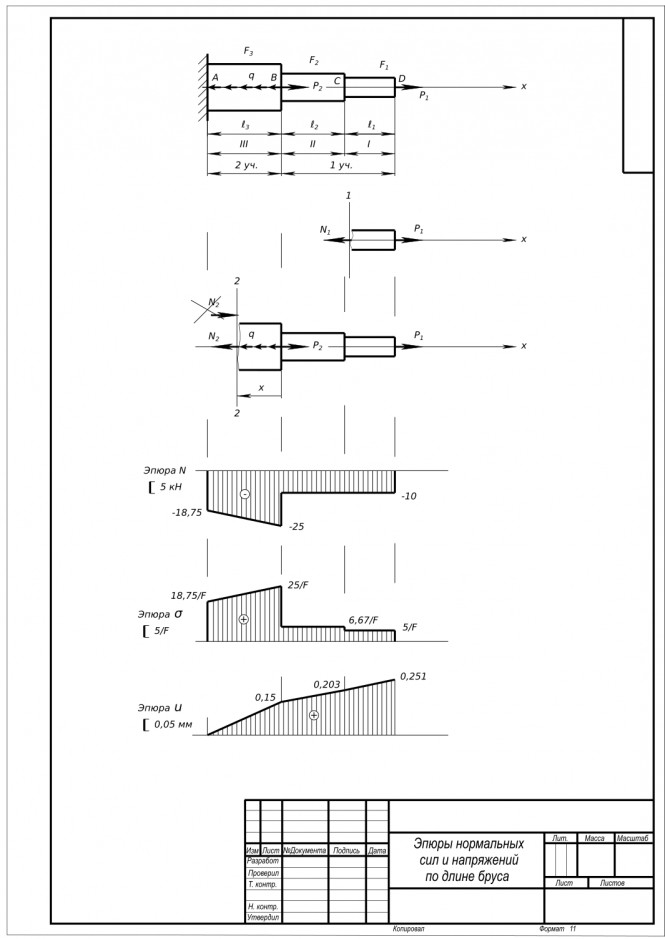 
Стальной ступенчатый брус заданной конфигурации подвергается воздействию внешней нагрузки q , P . Построить эпюру продольных сил 1. Построение эпюры продольных сил N Шаг 1. Вычертим эскиз модели: размеры d1; d2; d3 пропорциональны площадям сечений; , длины ступеней ℓ1; ℓ2; ℓ3 наносим на чертеж; брус закреплен в стене - закрепление "заделка". Шаг 2. Делим брус на участки нагружения (части бруса между внешними силами) - участки 1, 2. Шаг 3. Используем метод сечений для определения внутренних силовых факторов, действующих на каждом участке (при этом внутренние силы переходят в разряд внешних): Участок 1. Сумма проекций всех сил на ось X равна нулю.
$ ΣF_{x} = 0; P_{1} - N_{1} = 0; N_{1} = P_{1} = 10 кН $ Продольная сила N1 отрицательна. Участок 1 растянут. Участок 2. Сумма проекций всех сил на ось X равна нулю.
$ ΣF_{x} = 0; -qx + P_{1} + P_{2} + N_{2} = 0; N_{2} = qx - P_{1} - P_{2} $
$ x_{B} = 0; N_{2_{B}} = 0 - 10 - 15 = - 25 кН $ Продольная сила N2 со знаком минус, значит в действительности ее направление противоположно выбранному. Меняем направление N2B на чертеже, тогда
$ N_{2_{B}} = 25 кН $ Участок 2 в точке B растянут.
$ x_{A} = 0,25; N_{2_{A}} = 0,25×25 - 10 - 15 = - 18,75 кН $ Продольная сила N2 со знаком минус, значит в действительности ее направление противоположно выбранному. Меняем направление N2A на чертеже, тогда
$ N_{2_{A}} = 18,75 кН $ Участок 2 в точке A растянут. Шаг 3. Определяем величины нормальных напряжений по сечениям с учетом изменения площади поперечного сечения. Три участка по напряжениям:
$ σ_{1} = \frac{N_{1}}{F_{1}} = \frac{10}{2F} = \frac{5}{F} $
$ σ_{2} = \frac{N_{1}}{F_{2}} = \frac{N_{1}}{1,5F} = \frac{6,67}{F} $
$ σ_{3_{B}} = \frac{N_{2_{B}}}{F_{3}} = \frac{25}{F} $
$ σ_{3_{A}} = \frac{N_{2_{A}}}{F_{3}} = \frac{18,75}{F} $ Шаг 4. Если известны действующие силы и материал стержня, то требуемую площадь сечения находим из условия прочности бруса работающего на растяжение - сжатие:
$ σ_{3_{B}} = \frac{25000}{F}; F≥\frac{N}{[σ]} = \frac{25000}{160} = 156,25 мм^{2} $
$ F_{1} = 2F = 2×156,25=312,5 мм^{2} $
$ F_{2} = 1,5F = 1,5×156,25 = 234,68 мм^{2} $
$ F_{3} = F = 156,25 мм^{2} $ Шаг 5. На каждом участке определяем абсолютную деформацию (удлинение или сжатие):
$ u_{1} = \frac{σ_{1}L_{1}}{E} = \frac{(\frac{5000}{156,25})*0,3*10^{3}}{200*10^{3}} = 0,048 мм $
$ u_{2}=\frac{σ_{2}L_{2}}{E}=\frac{(\frac{6670}{156,25})*0,25*10^{3}}{200*10^{3}}=0,053 мм $
$ u_{3_{B}}=\frac{σ_{3_{B}}L_{3_{B}}}{E}=\frac{(\frac{25000}{156,25})*0,25*10^{3}}{200*10^{3}}=0,15 мм $
$ u_{3_{A}}=\frac{σ_{3_{A}}*L_{3_{A}}}{E}=\frac{(\frac{18750}{156,25})*0*10^{3}}{200*10^{3}}=0 мм $ Суммарное удлинение бруса (перемещение свободного конца)
$ u=u_{1}+u_{2}+u_{3_{B}}+u_{3_{A}}=0,048+0,053+0,15+0=0,251 мм $ Шаг 6. Построение эпюр внутренних силовых факторов, нормальных напряжений и перемещений по длине бруса. КомментарииОпределить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F, равная 2000 Н, длина бруса ℓ = 10 м; диаметр бруса d = 0,2 м. Вес бруса не учитывать. Для решения задачи построим эпюру внутренних изгибающих моментов и эпюру внутренней поперечной силы действующих в сечениях по длине балки. 
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой ℓ - длина балки Jx - момент инерции относительно главной центральной оси х E - модуль упругости материала балки EJx - изгибная жесткость Стержневая конструкция, все стержни которой лежат в одной плоскости и в этой же плоскости деформируются, называется плоской конструкцией. Вводим ортогональную систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки силой: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{A} - горизонтальная реакция Y_{A} - вертикальная реакция M_{RA} - угловая реакция (моментная реакция) Находим реакции, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю
$ ΣF_{y}=Y_{A}-F=0 $ из него находим вертикальную реакцию в опоре A
$ Y_{A}=F $ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю
$ ΣF_{z}=-Z_{A}=0 $ Из него находим горизонтальную реакцию в опоре A
$ Z_{A}=0 $ Третье уравнение - сумма всех моментов относительно точки A равна нулю
$ ΣM_{A}=-M_{RA}-F ℓ=0 $ Момент силы принято считать положительным, если он вращает балку против часовой стрелки и наоборот - если по часовой стрелке. Учитываем, что плечи реакций Y_{A} и Z_{A} равны нулю. из него (третьего уравнения) получаем угловую (моментную реакцию) в опоре A
$ M_{RA}=-F ℓ $ Рисуем силовую схему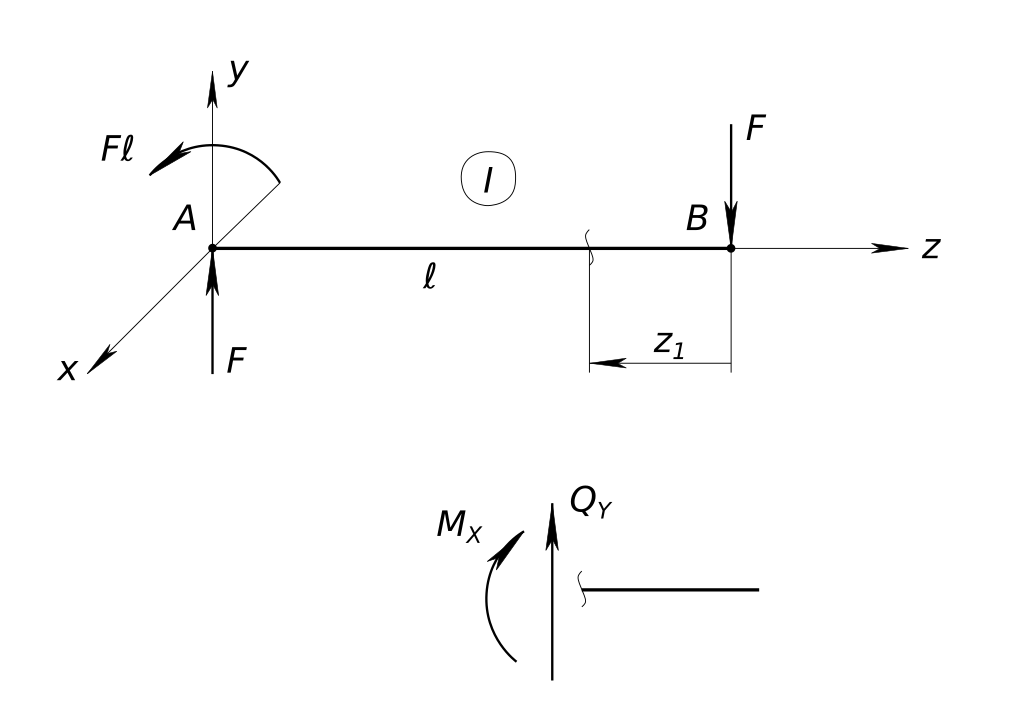 
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Четвертое (проверочное) уравнение - сумма всех моментов относительно точки B равна нулю
$ ΣM_{B}=-F ℓ+F ℓ=0 $ Далее разбиваем стержень на участки. Границами участка служат изменение сечения балки и точки приложения силовых факторов. Нагрузка приложена к концу балки. Изменения геометрии сечения балки нет. Получаем один участок. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезаем балку, отбрасываем левую часть. Заменяем действие отброшенной части силовыми факторами - Q_{y1}, M_{x1}. Пока не знаем их величину, но рисуем их в положительных направлениях, согласно установленному правилу знаков. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{1} равна нулю
$ ΣF_{y_{1}}=0=Q_{y_{1}}-F $ тогда
$ Q_{y_{1}}=F $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=-M_{x_{1}}-Fz_{1} $ тогда
$ M_{x_{1}}=-Fz_{1} $ В точке B
$ z_{1}=0; M_{x_{1}}=-F×0=0 $ В точке A
$ z_{1}=ℓ; M_{x_{1}}=-F ℓ $ Общепринято что: если слева от сечения рассматривается поперечная сила направленная вверх, то она положительна и наоборот если вниз; если справа от сечения рассматривается поперечная сила направленная вниз, то она положительна и наоборот если вверх. Изгибающий момент M_{x_{1}} найден со знаком минус. А это означает, что действительное направление RA противоположно принятому при составлении уравнения равновесия. Исправляем направление RA на расчетной схеме. Правило знаков при нахождении изгибающих моментов в сечениях балки: Если нижние слои балки растянуты, то найденный момент положительный, если наоборот - отрицательный. По полученным расчетам строим эпюры внутренних силовых факторов - эпюр поперечной силы и эпюр моментов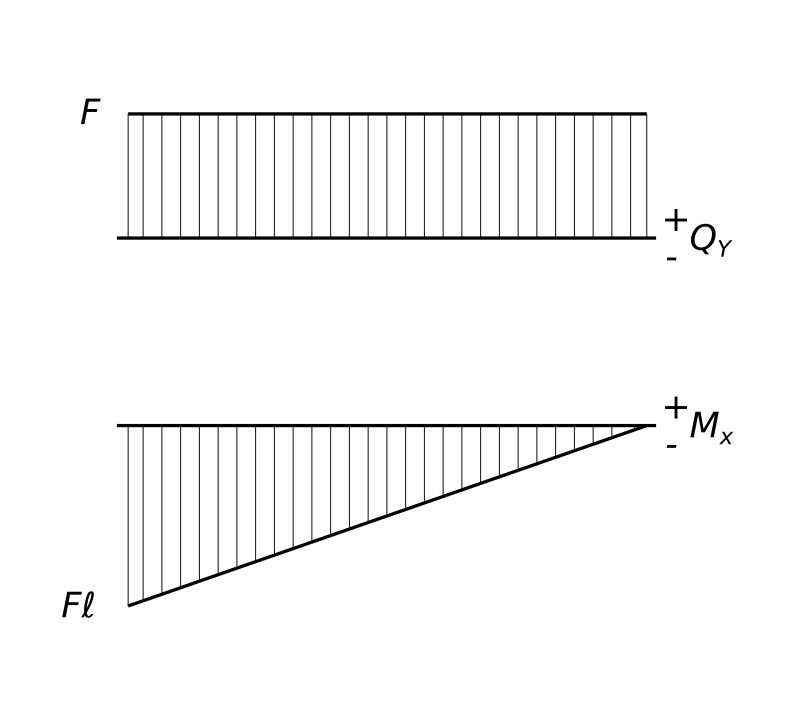 
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Эпюра поперечной силы Q_{y} выше с нулевой линии. Как видно из уравнения поперечной силы, ее значение не зависит от координаты z, характеризующей удаление сечения от концов участка. Поэтому, эпюра поперечной силы будет представлять собой горизонтальную прямую. Для ее построения необходима одна точка. Чтобы ее получить рассматривается сечение в произвольной точке участка. Как видно из уравнения момента, его значение зависит от координаты z, характеризующей удаление сечения от концов участка. Поэтому, эпюра момента представляет собой наклонную прямую. Для ее построения необходимы две точки. Чтобы их получить рассматриваются сечения на концах участка. В любом сечении поперечная сила равна Q_{y} = F. Эпюра моментов M_{x} показывает, что момент действующий на участке не постоянный и отрицательный его величина линейно возрастает от конца балки к ее заделке, достигая наибольшего значения равного
$ M_{x} = F ℓ $ максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой
$ σ = \frac{M_{x}}{W_{x}} $ Для круглого сечения бруса
$ W_{x} = \frac{πd^{3}}{32} $ максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой
$ σ = \frac{F ℓ}{\frac{πd^{3}}{32}} = $
$ = \frac{32×2000×10×1000}{π×200^{3}} = 25,46 \frac{Н}{мм^{2}} = 25,46 МПа $ КомментарииРасчет подшипников качения на заданный ресурс
Предварительно назначаем шариковые радиальные подшипники серии диаметров 2: 207. Схема установки подшипников - враспор. Для принятых подшипников из табл. 24.10 [1] находим:
$ C_{r} = 25500 Н; $
$ C_{0r} = 13700 Н; $
$ d=35 мм; D=72 мм; D_{ω}=11,112 мм; α = 0°. $ При установке вала на двух радиальных шариковых подшипниках осевая сила Fa, нагружающая подшипник, равна внешней осевой силе, действующей на вал.
$ F_{a] = F_{A} $ Для радиальных шарикоподшипников из условия равновесия вала следует:
$ F_{a1} = 0 Н; $
$ Fa2 = \frac{1}{2}FA = 0 Н . $
$ F_{A} = F_{a1} +F_{a2} = 0 Н . $ Дальнейший расчет производим для более нагруженного подшипника опоры 2. Отношение
$ \frac{D_{ω}cosα}{D_{pω}} = \frac{11,112×1}{53,5} = 0,2077, $ где
$ D_{pω} =0,5(D+d)=0,5(72+35)=53,5 мм. $ В соответствии с табл. 7.3 имеем
$ f_{0}=13,7 $ Коэффициент осевого нагружения (см. табл. 7.2)
$ e=0,28(\frac{f_{0}F_{a}}{C_{0r}})^{0,23}=0,28(\frac{13,7×0}{13700})^{0,23}=0 $ Отношение
$ \frac{F_{a}}{VF_{r}} = \frac{0}{1×920} = 0 $ что больше e=0 (V=1 при вращении внутреннего кольца). Окончательно принимаем (см. табл. 7.2): X=0,56; Y=0,44/e Принимаем Kб =1,4 [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o). Эквивалентная динамическая радиальная нагрузка
$ P_{r} = (VXF_{r} + YF_{a})K_{б}K_{т}= $
$ = (1 × 0,56 × 920 + Y × 0) × 1,4 × 1 = 721 Н. $ Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
$ L10ah = a_{1}a_{23}(\frac{C_{r}}{P_{r}})^{k}(\frac{10^{6}}{60n}) = $
$ = 1 × 0.7 × (\frac{25500}{721})^{3}×(\frac{10^{6}}{60×291}) = 1773653 ч. $ Так как расчетный ресурс больше требуемого:
$ L10ah > L'10ah (1773653 > 33533.28) $ то предварительно назначенный подшипник 207 пригоден. При требуемом ресурсе 90%. КомментарииРасчет подшипников качения на заданный ресурс
Расчет подшипников качения на заданный ресурс. Промежуточный вал.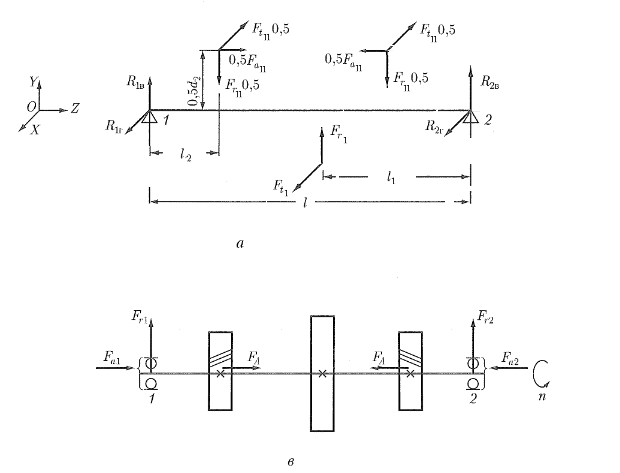 
Расчет подшипников качения на заданный ресурс ℓ=192 мм; ℓ1=96 мм; ℓ2=36,5 мм; 1. Радиальные реакции опор от сил в зацеплении: в плоскости YOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{r2}ℓ_{2}+F_{r2}(ℓ - ℓ_{2}) – F_{r1}ℓ_{1} – R_{2в}ℓ=0; $
$ R_{2в}=(F_{r2}ℓ_{2}+F_{r2}(ℓ – ℓ_{2}) – F_{r1}ℓ_{1})/ℓ= $
$ = \frac{947,5×36,5+947,5(192 – 36,5) – 713,1×96}{192} = 591 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2} = 0; R_{1в}ℓ + F_{r1}ℓ_{1} – F_{r2}(ℓ – ℓ_{2}) – F_{r2}ℓ_{2}=0; $
$ R_{1в} = \frac{F_{r2}ℓ – F_{r1}ℓ_{1}}{ℓ} = $
$ =\frac{(947,5×192 – 713,1×96)}{192} = 591 Н $ Проверка. Сумма проекций всех сил на ось Y равна нулю
$ ΣY=R_{1в} – 0,5F_{rII}+F_{rI} – 0,5F_{rII}+R_{2в} = $
$ = 591 – 1×1895+713+591=0 $ Реакции опор определены правильно. в плоскости XOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; R_{2г}ℓ+F_{tI}ℓ_{1} – 0,5F_{tII}ℓ_{2} – 0,5F_{tII}(ℓ – ℓ_{2})=0 $
$ R_{2г}=\frac{0,5F_{tII}ℓ – F_{tI}ℓ_{1}}{ℓ} = $
$ =\frac{0,5×5025×192 – 1959×96}{192}=1533 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2} = 0; 0,5F_{tII}(ℓ – ℓ_{2})+0,5F_{tII}ℓ_{2} – F_{tI}ℓ_{1} – R_{1г}ℓ=0 $
$ R_{1г} = \frac{0,5F_{tII}ℓ – F_{tI}ℓ_{1}}{ℓ} = $
$ =\frac{0,5×5025×192-1959×96}{192}=1533 Н $ Проверка. Сумма проекций всех сил на ось X равна нулю
$ ΣX=R_{1г} - 0,5F_{tII} – 0,5F_{tII} + F_{tI} + R_{2г} = $
$ = 1533 – 5025+1959+1533 = 0 $ 2. Радиальные реакции опор от действия муфты (на II валу муфты нет) 3. Реакции опор для расчета подшипников:
$ F_{r1max} = R_{1} = ((R_{1в})^{2} + (R_{1г})^{2})^{0,5} = $
$ = (591^{2} + 1533^{2})^{0,5} = 1643 Н; $
$ F_{r2max} = R_{2} = ((R_{2в})^{2} + (R_{2г})^{2})^{0,5} = $
$ = (591^{2} + 1533^{2})^{0,5} = 1643 Н; $ Внешняя осевая сила действующая на вал
$ F_{Amax} = F_{a} = 0 Н $ 4. Для типового режима нагружения III коэффициент эквивалентности KE = 0,56. Вычисляем эквивалентные нагрузки:
$ F_{r1} = K_{E}F_{r1max} = 0,56 × 1643 = 920 Н; $
$ F_{r2} = K_{E}F_{r2max} = 0,56 × 1643 = 920 Н; $
$ F_{A} = K_{E}F_{Amax} = 0,56 × 0 = 0 Н. $ Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии