Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Создано:
@nick
30 апреля 2020
15:02
Создано:
@nick
30 апреля 2020
15:02
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F, равная 2000 Н, длина бруса ℓ = 10 м; диаметр бруса d = 0,2 м. Вес бруса не учитывать. 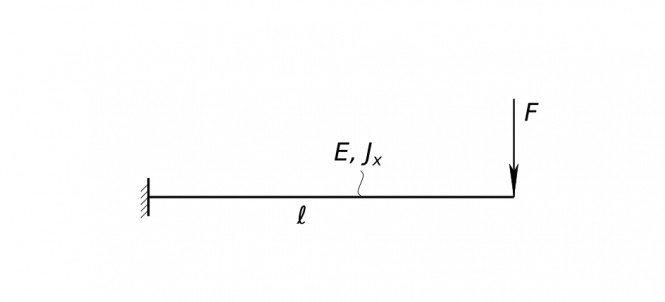
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Решения задачиОпределить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F, равная 2000 Н, длина бруса ℓ = 10 м; диаметр бруса d = 0,2 м. Вес бруса не учитывать. Для решения задачи построим эпюру внутренних изгибающих моментов и эпюру внутренней поперечной силы действующих в сечениях по длине балки. 
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой ℓ - длина балки Jx - момент инерции относительно главной центральной оси х E - модуль упругости материала балки EJx - изгибная жесткость Стержневая конструкция, все стержни которой лежат в одной плоскости и в этой же плоскости деформируются, называется плоской конструкцией. Вводим ортогональную систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки силой: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{A} - горизонтальная реакция Y_{A} - вертикальная реакция M_{RA} - угловая реакция (моментная реакция) Находим реакции, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю
$ ΣF_{y}=Y_{A}-F=0 $ из него находим вертикальную реакцию в опоре A
$ Y_{A}=F $ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю
$ ΣF_{z}=-Z_{A}=0 $ Из него находим горизонтальную реакцию в опоре A
$ Z_{A}=0 $ Третье уравнение - сумма всех моментов относительно точки A равна нулю
$ ΣM_{A}=-M_{RA}-F ℓ=0 $ Момент силы принято считать положительным, если он вращает балку против часовой стрелки и наоборот - если по часовой стрелке. Учитываем, что плечи реакций Y_{A} и Z_{A} равны нулю. из него (третьего уравнения) получаем угловую (моментную реакцию) в опоре A
$ M_{RA}=-F ℓ $ Рисуем силовую схему 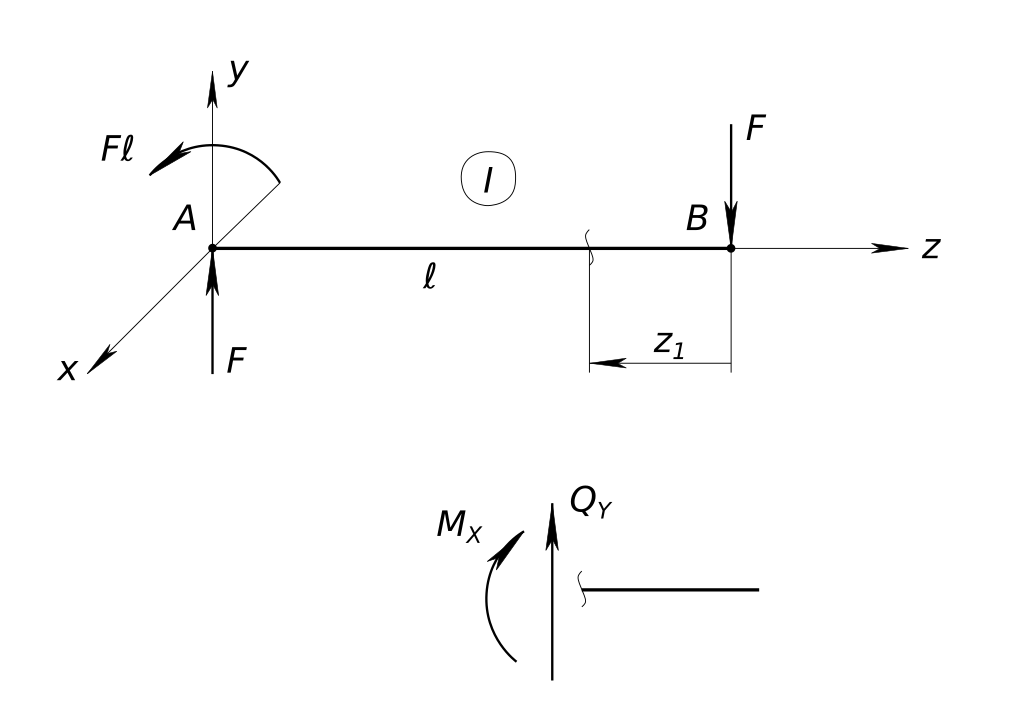
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Четвертое (проверочное) уравнение - сумма всех моментов относительно точки B равна нулю
$ ΣM_{B}=-F ℓ+F ℓ=0 $ Далее разбиваем стержень на участки. Границами участка служат изменение сечения балки и точки приложения силовых факторов. Нагрузка приложена к концу балки. Изменения геометрии сечения балки нет. Получаем один участок. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезаем балку, отбрасываем левую часть. Заменяем действие отброшенной части силовыми факторами - Q_{y1}, M_{x1}. Пока не знаем их величину, но рисуем их в положительных направлениях, согласно установленному правилу знаков. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{1} равна нулю
$ ΣF_{y_{1}}=0=Q_{y_{1}}-F $ тогда
$ Q_{y_{1}}=F $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=-M_{x_{1}}-Fz_{1} $ тогда
$ M_{x_{1}}=-Fz_{1} $ В точке B
$ z_{1}=0; M_{x_{1}}=-F×0=0 $ В точке A
$ z_{1}=ℓ; M_{x_{1}}=-F ℓ $ Общепринято что: если слева от сечения рассматривается поперечная сила направленная вверх, то она положительна и наоборот если вниз; если справа от сечения рассматривается поперечная сила направленная вниз, то она положительна и наоборот если вверх. Изгибающий момент M_{x_{1}} найден со знаком минус. А это означает, что действительное направление RA противоположно принятому при составлении уравнения равновесия. Исправляем направление RA на расчетной схеме. Правило знаков при нахождении изгибающих моментов в сечениях балки: Если нижние слои балки растянуты, то найденный момент положительный, если наоборот - отрицательный. По полученным расчетам строим эпюры внутренних силовых факторов - эпюр поперечной силы и эпюр моментов 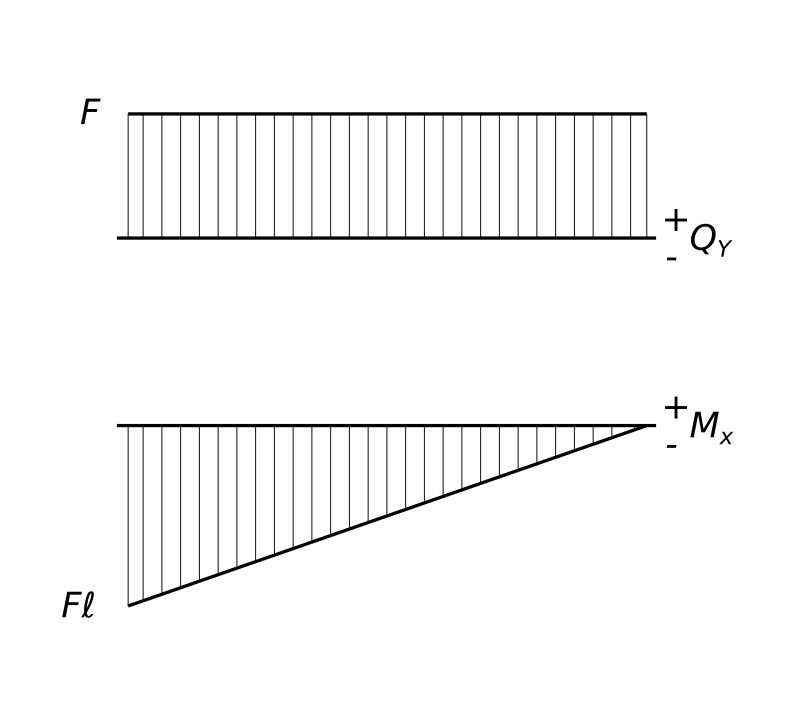
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой Эпюра поперечной силы Q_{y} выше с нулевой линии. Как видно из уравнения поперечной силы, ее значение не зависит от координаты z, характеризующей удаление сечения от концов участка. Поэтому, эпюра поперечной силы будет представлять собой горизонтальную прямую. Для ее построения необходима одна точка. Чтобы ее получить рассматривается сечение в произвольной точке участка. Как видно из уравнения момента, его значение зависит от координаты z, характеризующей удаление сечения от концов участка. Поэтому, эпюра момента представляет собой наклонную прямую. Для ее построения необходимы две точки. Чтобы их получить рассматриваются сечения на концах участка. В любом сечении поперечная сила равна Q_{y} = F. Эпюра моментов M_{x} показывает, что момент действующий на участке не постоянный и отрицательный его величина линейно возрастает от конца балки к ее заделке, достигая наибольшего значения равного
$ M_{x} = F ℓ $ максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой
$ σ = \frac{M_{x}}{W_{x}} $ Для круглого сечения бруса
$ W_{x} = \frac{πd^{3}}{32} $ максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой
$ σ = \frac{F ℓ}{\frac{πd^{3}}{32}} = $
$ = \frac{32×2000×10×1000}{π×200^{3}} = 25,46 \frac{Н}{мм^{2}} = 25,46 МПа $ КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии