Расчет подшипников качения на заданный ресурс Создано:
@nick
24 марта 2020
13:06
Создано:
@nick
24 марта 2020
13:06
Расчет подшипников качения на заданный ресурс. Исходные данные для расчета: частота вращения вала n = 1445 мин-1; требуемый ресурс при вероятности безотказной работы 90%: L'10ah = 33533,28 ч.; диаметр посадочных поверхностей вала d = 35 мм; максимальные длительно действующие силы: Ft = 1959 Н, Fr = 713,1 Н, FA= 0 Н; режим нагружения - III - средний нормальный; ожидаемая температура работы tраб = 50oC. На входном валу редуктора предполагается установка упругой муфты со стальными стержнями, номинальный вращающий момент по каталогу TH=1720 Нм. Допустимое радиальное смещение соединяемых муфтой валов при монтаже ∆=0,25 мм. Делительные диаметры
Решения задачиРасчет подшипников качения на заданный ресурс. Входной вал. 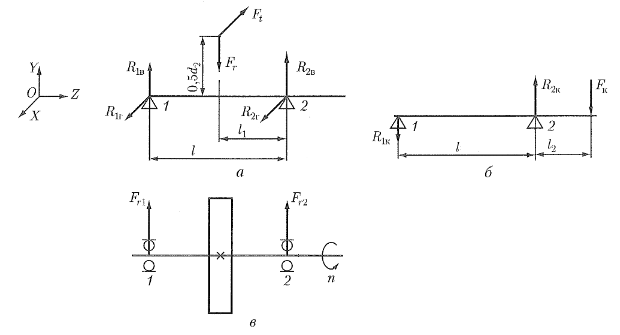
Расчет подшипников качения на заданный ресурс Линейные размеры: ℓ=192 мм; ℓ1=96 мм; ℓ2=80 мм; d1=52,5 мм. 1. Радиальные реакции опор от сил в зацеплении: в плоскости YOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{r}(ℓ-ℓ_{1}) + \frac{F_{a}d_{1}}{2} – R_{2в}ℓ=0; $
$ R_{2в}=\frac{F_{r}(ℓ-ℓ_{1})+\frac{F_{a}d_{1}}{2}}{ℓ}= $
$ = \frac{713,1(192-96)+0}{192}=356,55 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2}=0; R_{1в}ℓ + \frac{F_{a}d_{1}}{2} – F_{r}ℓ_{1}=0; $
$ R_{1в}=\frac{F_{r}ℓ_{1}- \frac{F_{a}d_{1}}{2}}{ℓ}= $
$ = \frac{713,1×96-0}{192}=356,55 Н; $ Проверка: Сумма проекций всех сил на ось Y равны нулю
$ ΣY=R_{1в} – F_{r} + R_{2в}=356,55 – 713,1 + 356,55 = 0; $ Значит реакции найдены правильно. в плоскости XOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; R_{2г}ℓ — F_{t}(ℓ-ℓ_{1})=0; $
$ R_{2г} = \frac{F_{t}(ℓ-ℓ_{1})}{ℓ}= \frac{1959(192-96)}{192}=979,5 Н; $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2}=0; - R_{1г}ℓ + F_{t}ℓ_{1} = 0; $
$ R_{1г} = \frac{F_{t}ℓ_{1}}{ℓ} =\frac{1959×96}{192} = 979,5 Н; $ Проверка: Сумма проекций всех сил на ось X равны нулю
$ ΣX= R_{1г} – F_{t} +R_{2г} = 979,5 -1959 +979,5 = 0; $ Реакции найдены правильно. Суммарные реакции опор:
$ R_{1} = (R_{1г}^{2}+ R_{1в}^{2})^{0,5} = $
$ (979,5^{2} + 356,55^{2})^{0,5} = 1042,38 Н; $
$ R_{2} = (R_{2г}^{2}+ R_{2в}^{2})^{0,5} = $
$ (979,5^{2} + 356,55^{2})^{0,5} = 1042,38 Н; $ Комментарии2. Радиальные реакции опор от действия муфты. Радиальная жесткость муфты МУВП
$ C_{p} = 610 T_{H}^{0,333} = 610 × 51,4^{0,333} = 2267,74 Н/мм $ Радиальная сила Fк на валу от упругой муфты
$ F_{к} = C_{p} ∆ = 2267,74 × 0,3 = 680,32 Н $ Реакции от силы Fк Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{к}(ℓ +ℓ_{2}) — R_{2к}ℓ = 0; $
$ R_{2к}= \frac{F_{к}(ℓ +ℓ_{2})}{ℓ}=\frac{680,32(192+80)}{192} = 963,79 Н; $
$ ΣM_{2}=0; F_{к}ℓ_{2} — R_{1к}ℓ = 0; $
$ R_{1к}= \frac{F_{к}ℓ_{2}}{ℓ}= \frac{680,32×80}{192} = 283,47 Н; $ Проверка:
$ — F_{к} +R_{2к}-R_{1к}= — 680,32 + 963,79 — 283,47 = 0; $ Реакции найдены правильно. 3. Реакции опор для расчета подшипников:
$ F_{r1max} = R_{1} + R_{1к} = 1042,38 + 283,47 = 1325,85 Н; $
$ F_{r2max} = R_{2} + R_{2к} = 1042,38 + 963,79 = 2006,17 Н; $ Внешняя осевая сила действующая на вал,
$ F_{Amax} = F_{a} = 0 Н $ 4. Для типового режима нагружения III коэффициент эквивалентности
$ K_{E} = 0,56 $ Вычисляем эквивалентные нагрузки:
$ F_{r1} = K_{E}F_{r1max} = 0,56 ∙ 1325,85 = 742 Н; $
$ F_{r2} = K_{E}F_{r2max} = 0,56 ∙ 2006,17 = 1123 Н; $
$ F_{A} = K_{E}F_{Amax} = 0,56 × 0 = 0 Н. $ 5. Предварительно назначаем шариковые радиальные подшипники серии диаметров 2: 207. Схема установки подшипников - враспор. 6. Для принятых подшипников из табл. 24.10 [1] находим: Cr = 25500 Н; C0r = 13700 Н; d=35 мм; D=72 мм; Dω=11,112 мм; α = 0°. 7. При установке вала на двух радиальных шариковых подшипниках осевая сила Fa, нагружающая подшипник, равна внешней осевой силе, действующей на вал. Fa = FA Для радиальных шарикоподшипников из условия равновесия вала следует: Fa1 = 0; Fa2 = FA = 0. Дальнейший расчет производим для более нагруженного подшипника опоры 2. 8. Отношение Dωcosα/Dpω = 11,112∙1/53,5 = 0,2077, где Dpω =0,5(D+d)=0,5(72+35)=53,5 мм. В соответствии с табл. 7.3 имеем f0=13,7 Коэффициент осевого нагружения (см. табл. 7.2) e=0,28(f0Fa/C0r)0,23=0,28(13,7×0/13700)0,23=0 9. Отношение Fa/(VFr)=0/(1×1123)=0, что больше e=0 (V=1 при вращении внутреннего кольца). Окончательно принимаем (см. табл. 7.2): X=0,56; Y=0,44/e 10. Принимаем Kб =1,4 [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o). Эквивалентная динамическая радиальная нагрузка
$ P_{r} = (VXF_{r} + YF_{a})K_{б}K_{т}= $
$ = (1 × 0,56 × 1123 + Y × 0) × 1,4 × 1 = 880 Н $ 11. Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
$ L10ah = a_{1}a_{23}(\frac{C_{r}}{P_{r}})k(\frac{10^{6}}{60n}) = $
$ = 1 × 0,7 × (\frac{25500}{880} )^{3}×(\frac{10^{6}}{60×1445}) = 196450 ч. $ 6. Так как расчетный ресурс больше требуемого: L10ah > L'10ah (196450 > 33533,28), то предварительно назначенный подшипник 207 пригоден. При требуемом ресурсе 90%. КомментарииРасчет подшипников качения на заданный ресурс. Промежуточный вал. 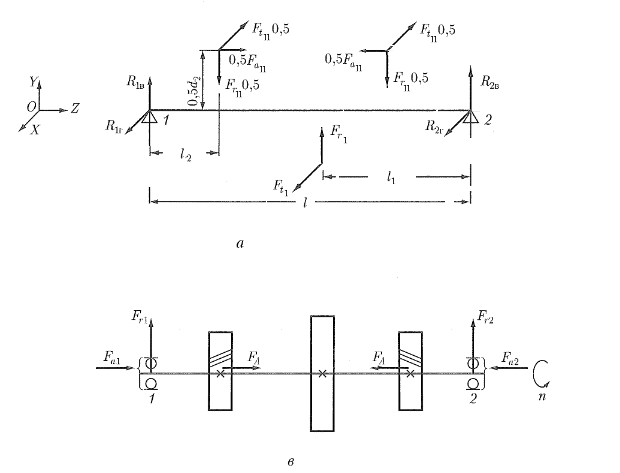
Расчет подшипников качения на заданный ресурс ℓ=192 мм; ℓ1=96 мм; ℓ2=36,5 мм; 1. Радиальные реакции опор от сил в зацеплении: в плоскости YOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; F_{r2}ℓ_{2}+F_{r2}(ℓ - ℓ_{2}) – F_{r1}ℓ_{1} – R_{2в}ℓ=0; $
$ R_{2в}=(F_{r2}ℓ_{2}+F_{r2}(ℓ – ℓ_{2}) – F_{r1}ℓ_{1})/ℓ= $
$ = \frac{947,5×36,5+947,5(192 – 36,5) – 713,1×96}{192} = 591 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2} = 0; R_{1в}ℓ + F_{r1}ℓ_{1} – F_{r2}(ℓ – ℓ_{2}) – F_{r2}ℓ_{2}=0; $
$ R_{1в} = \frac{F_{r2}ℓ – F_{r1}ℓ_{1}}{ℓ} = $
$ =\frac{(947,5×192 – 713,1×96)}{192} = 591 Н $ Проверка. Сумма проекций всех сил на ось Y равна нулю
$ ΣY=R_{1в} – 0,5F_{rII}+F_{rI} – 0,5F_{rII}+R_{2в} = $
$ = 591 – 1×1895+713+591=0 $ Реакции опор определены правильно. в плоскости XOZ Сумма моментов всех сил относительно опоры 1
$ ΣM_{1}=0; R_{2г}ℓ+F_{tI}ℓ_{1} – 0,5F_{tII}ℓ_{2} – 0,5F_{tII}(ℓ – ℓ_{2})=0 $
$ R_{2г}=\frac{0,5F_{tII}ℓ – F_{tI}ℓ_{1}}{ℓ} = $
$ =\frac{0,5×5025×192 – 1959×96}{192}=1533 Н $ Сумма моментов всех сил относительно опоры 2
$ ΣM_{2} = 0; 0,5F_{tII}(ℓ – ℓ_{2})+0,5F_{tII}ℓ_{2} – F_{tI}ℓ_{1} – R_{1г}ℓ=0 $
$ R_{1г} = \frac{0,5F_{tII}ℓ – F_{tI}ℓ_{1}}{ℓ} = $
$ =\frac{0,5×5025×192-1959×96}{192}=1533 Н $ Проверка. Сумма проекций всех сил на ось X равна нулю
$ ΣX=R_{1г} - 0,5F_{tII} – 0,5F_{tII} + F_{tI} + R_{2г} = $
$ = 1533 – 5025+1959+1533 = 0 $ 2. Радиальные реакции опор от действия муфты (на II валу муфты нет) 3. Реакции опор для расчета подшипников:
$ F_{r1max} = R_{1} = ((R_{1в})^{2} + (R_{1г})^{2})^{0,5} = $
$ = (591^{2} + 1533^{2})^{0,5} = 1643 Н; $
$ F_{r2max} = R_{2} = ((R_{2в})^{2} + (R_{2г})^{2})^{0,5} = $
$ = (591^{2} + 1533^{2})^{0,5} = 1643 Н; $ Внешняя осевая сила действующая на вал
$ F_{Amax} = F_{a} = 0 Н $ 4. Для типового режима нагружения III коэффициент эквивалентности KE = 0,56. Вычисляем эквивалентные нагрузки:
$ F_{r1} = K_{E}F_{r1max} = 0,56 × 1643 = 920 Н; $
$ F_{r2} = K_{E}F_{r2max} = 0,56 × 1643 = 920 Н; $
$ F_{A} = K_{E}F_{Amax} = 0,56 × 0 = 0 Н. $ КомментарииПредварительно назначаем шариковые радиальные подшипники серии диаметров 2: 207. Схема установки подшипников - враспор. Для принятых подшипников из табл. 24.10 [1] находим:
$ C_{r} = 25500 Н; $
$ C_{0r} = 13700 Н; $
$ d=35 мм; D=72 мм; D_{ω}=11,112 мм; α = 0°. $ При установке вала на двух радиальных шариковых подшипниках осевая сила Fa, нагружающая подшипник, равна внешней осевой силе, действующей на вал.
$ F_{a] = F_{A} $ Для радиальных шарикоподшипников из условия равновесия вала следует:
$ F_{a1} = 0 Н; $
$ Fa2 = \frac{1}{2}FA = 0 Н . $
$ F_{A} = F_{a1} +F_{a2} = 0 Н . $ Дальнейший расчет производим для более нагруженного подшипника опоры 2. Отношение
$ \frac{D_{ω}cosα}{D_{pω}} = \frac{11,112×1}{53,5} = 0,2077, $ где
$ D_{pω} =0,5(D+d)=0,5(72+35)=53,5 мм. $ В соответствии с табл. 7.3 имеем
$ f_{0}=13,7 $ Коэффициент осевого нагружения (см. табл. 7.2)
$ e=0,28(\frac{f_{0}F_{a}}{C_{0r}})^{0,23}=0,28(\frac{13,7×0}{13700})^{0,23}=0 $ Отношение
$ \frac{F_{a}}{VF_{r}} = \frac{0}{1×920} = 0 $ что больше e=0 (V=1 при вращении внутреннего кольца). Окончательно принимаем (см. табл. 7.2): X=0,56; Y=0,44/e Принимаем Kб =1,4 [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o). Эквивалентная динамическая радиальная нагрузка
$ P_{r} = (VXF_{r} + YF_{a})K_{б}K_{т}= $
$ = (1 × 0,56 × 920 + Y × 0) × 1,4 × 1 = 721 Н. $ Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
$ L10ah = a_{1}a_{23}(\frac{C_{r}}{P_{r}})^{k}(\frac{10^{6}}{60n}) = $
$ = 1 × 0.7 × (\frac{25500}{721})^{3}×(\frac{10^{6}}{60×291}) = 1773653 ч. $ Так как расчетный ресурс больше требуемого:
$ L10ah > L'10ah (1773653 > 33533.28) $ то предварительно назначенный подшипник 207 пригоден. При требуемом ресурсе 90%. КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии