Расчетно Графические Работы Активность в теме Расчетно Графические РаботыСамые активные инженеры в теме Расчетно Графические РаботыЛучшие решения в теме Расчетно Графические РаботыПостроить эпюры продольных сил и нормальных напряжений по длине бруса
Двух ступенчатый стальной брус нагружен силами: F1=20 кН; F2=10 кН; F3=5 кН. Площади поперечных сечений бруса: A1=1,8 см2; A2=3,2 см2. a=0,2 м. Принять E=2х100000 МПа, [σ]=160 МПа. Построить эпюры продольных сил, нормальных напряжений. Определить перемещение конца бруса. 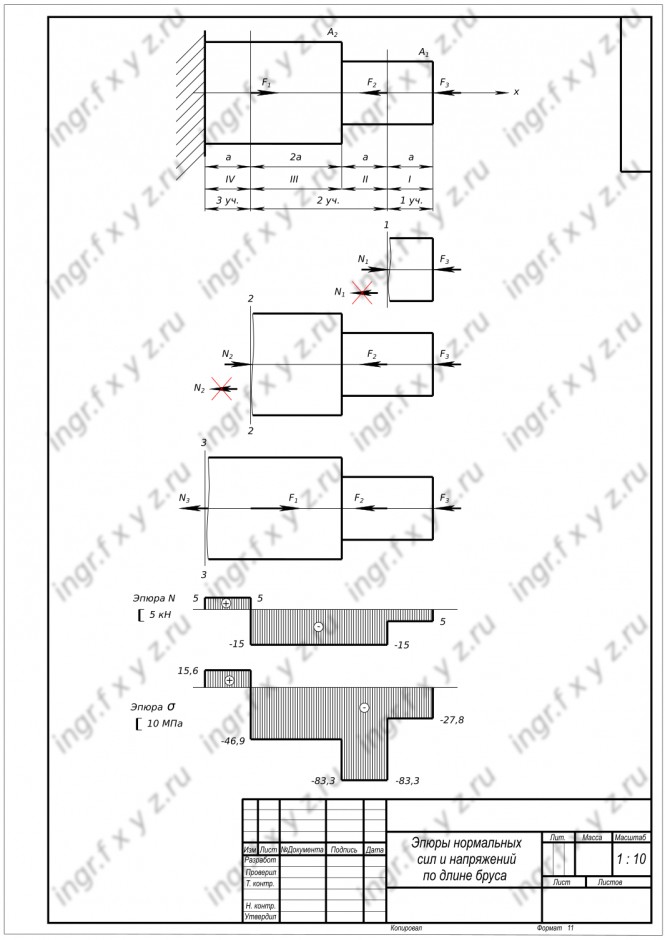
Двух ступенчатый стальной брус нагружен силами: F1=20 кН; F2=10 кН; F3=5 кН. Площади поперечных сечений бруса: A1=1,8 см2; A2=3,2 см2. a=0,2 м. Принять E=2х100000 Н/мм2. Построить эпюры нормальных сил и напряжений по длине бруса. Определить перемещение конца бруса. Брус закреплен в стене - закрепление заделка. Сечения бруса круглой формы
$ A = \frac{πd^{2}}{4} $ Находим диаметры ступеней бруса.
$ d = \sqrt{\frac{4A}{π}} $
$ d_{1}=15,14 мм; d_{2}=20,19 мм $ Делим брус на участки нагружения (части бруса между внешними силами) - участки 1, 2 и 3. Используем метод сечений для определения внутренних силовых факторов, действующих на каждом участке (при этом внутренние силы переходят в разряд внешних): Участок 1. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-N_{1}=0; N_{1}=-F_{3}= -5 кН $ Продольная сила N1 Знак минус означает, что действительное направление N1 противоположно первоначально выбранному.. Участок 1 сжат. Участок 2. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-F_{2}-N_{2}=0; N_{2}=-F_{3}-F_{2}=-5-10= -15 кН $ Продольная сила N2 отрицательна. Знак минус означает, что действительное направление N2 противоположно первоначально выбранному. Участок 2 сжат. Участок 3. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-F_{2}+F_{1}-N_{3}=0; N_{3}=20 - 5 -10= 5 кН $ Продольная сила N3 положительна. Это означает, что действительное направление N3 совпадает с первоначально выбранным. Участок 3 растянут. Определяем величины нормальных напряжений по сечениям с учетом изменения площади поперечного сечения. Четыре участка по напряжениям:
$ σ_{1} =\frac{N_{1}}{A_{1}}=\frac{5×10^{3}}{1,8×100}=27,8 \frac{Н}{мм^{2}}=27,8 МПа $
$ σ_{2} =\frac{N_{2}}{A_{1}}=\frac{15×10^{3}}{1,8×100}=83,3 МПа $
$ σ_{3} =\frac{N_{2}}{A_{2}}=\frac{15×10^{3}}{3,2×100}=46,9 МПа $
$ σ_{4} =\frac{N_{3}}{A_{2}}=\frac{5×10^{3}}{3,2×100}=15,6 МПа $ Строим эпюры продольных сил и эпюру нормальных напряжений, полагая растягивающие напряжения положительными. Эпюра продольных сил показывает изменение внутреннего силового фактора по длине бруса: участки I, II и III испытывают деформацию сжатия; участок IV испытывает деформацию растяжения. Эпюра нормальных напряжений показывает их изменение по длине бруса. Наиболее опасным участком является участок II. Так как нормальные напряжения на нем максимальны по величине σII=83,3 МПа Проверяем прочность бруса работающего на растяжение - сжатие: по условию прочности $ |σ_{max}=83,3 МПа|≤[σ=160 МПа] $ Прочность обеспечена. На каждом участке определяем абсолютную деформацию (удлинение или сжатие):
$ ∆ℓ_{1} = \frac{σ_{1}L_{1}}{E}=\frac{-27,8×10^{3}×0,2}{200×10^{3}}=-0,028 мм $
$ ∆ℓ_{2} = \frac{σ_{2}L_{2}}{E}=\frac{-83,3×10^{3}×0,2}{200×10^{3}}=-0,083 мм $
$ ∆ℓ_{3} = \frac{σ_{3}L_{3}}{E}=\frac{-46,9×10^{3}×0,4}{200×10^{3}}=-0,094 мм $
$ ∆ℓ_{4} = \frac{σ_{4}L_{4}}{E}=\frac{15,6×10^{3}×0,2}{200×10^{3}}=0,016 мм $ Суммарное удлинение бруса (перемещение свободного конца)
$ ∆ℓ=∆ℓ_{1}+∆ℓ_{2}+∆ℓ_{3}+∆ℓ_{4}=-0,189 мм $ Определить центр тяжести плоской фигуры
Определить центр тяжести плоской фигуры 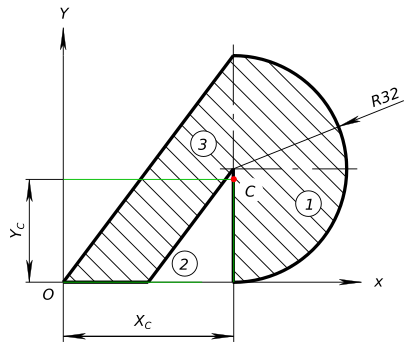
Определить центр тяжести плоской фигуры Расчетно графическую работу выполняем по следующему алгоритму: - выбираем рациональное направление осей X и Y. Данная плоская фигура не имеет осей симметрии, поэтому ось X проводим по основанию (нижней границе) фигуры и ось Y - по крайней левой точке (границе); - разбиваем сложную фигуру на простые: 1 - полукруг; 2 - треугольник; 3 - треугольник; - определяем координаты их центров тяжести. 1 - полукруг R32
$ X_{C_{1}} = 24+24+\frac{4}{3}\frac{R}{π}=48+\frac{4}{3}×\frac{32}{3,14}=61,58 мм $
$ Y_{C_{1}} = 32 мм $ 2 - треугольник
$ X_{C_{2}} = 24+24-\frac{1}{3}×24=40 мм $
$ Y_{C_{2}} =\frac{1}{3}×\frac{R}{1}=\frac{1}{3}×\frac{32}{2}= 10,67 мм $ 3 - треугольник
$ X_{C_{3}} = 48 - \frac{1}{3}×(24+24)= 32 мм $
$ Y_{C_{3}} = \frac{1}{3}×2R=\frac{1}{3}×2×32=21,33 мм $ - Определяем площади простых фигур входящих в сложную; 1 - полукруг R32
$ A_{1}=\frac{1}{2}×πR^{2} = \frac{1}{2}×3,14×32×32=1608,50 мм^{2} $ 2 - треугольник с катетами 24 мм и 32 мм.
$ A_{2} = \frac{1}{2}(24×32)=384 мм^{2} $ 3 - треугольник с катетами 48 мм и 64 мм.
$ A_{3} = \frac{1}{2}((24+24)×2×32)=1536 мм^{2} $ - Определяем координаты центра тяжести плоской фигуры
$ X_{C} = \frac{ΣA_{i}X_{i}}{ΣA_{i}}= $
$ = \frac{1608,50×61,58-384×40+1536×32}{1608,50-384+1536}=48,12 мм $
$ Y_{C} = \frac{ΣA_{i}Y_{i}}{ΣA_{i}}= $
$ = \frac{1608,50×32-384×10,67+1536×21,33}{1608,50-384+1536}=29,03 мм $ - Отмечаем положение центра тяжести фигуры на чертеже. КомментарииПланы скоростей и ускорений.
Пример текста Комментарии@nick нужна ваша помощь. Срочно.
Nick, сможете это сделать?
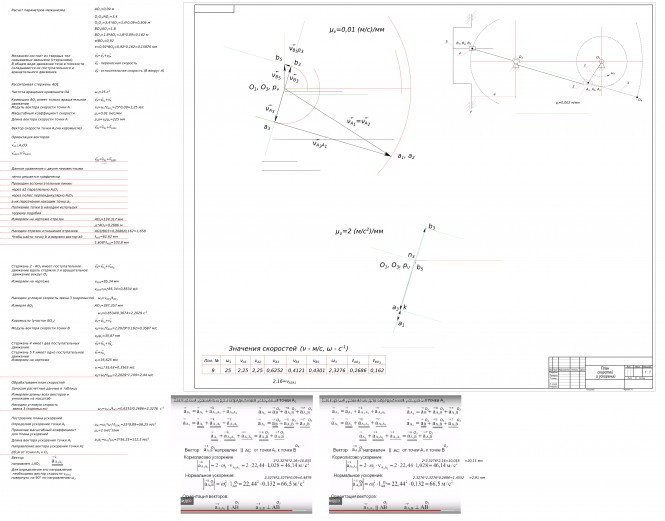
Планы скоростей и ускорений.
Сделать планы скоростей и ускорений для девятого положения КомментарииЗдравствуйте nick, сегодня будут планы ускорений?
Я работаю над этим вопросом, но пока еще трудно получается. Не могу ничего обещать.
То есть ещё остался план для 2го положения?
Планы скоростей готовы, остались планы ускорений
Добрый день! А почему на втором чертеже два плана?
Ещё остался план ускорения для второго положения?
Nick, добрый день, А когда ускорения будут готовы?
А на этом чертеже план скоростей и ускорений для 9го?
Планы скоростей и ускорений.
Сделать планы скоростей и ускорений для второго положения КомментарииПривет, увидел ваш закреп, спасибо большое за работу!!!
Сложнейшие задачи в теме Расчетно Графические Работы24 марта 2020 13:06
0 подписчиков
1060 просмотров
4
решения 10 марта 2023 09:20
0 подписчиков
201 просмотр
1
решение 3 марта 2020 09:50
0 подписчиков
989 просмотров
1
решение 13 марта 2020 08:08
0 подписчиков
838 просмотров
1
решение 2 мая 2020 12:17
0 подписчиков
1603 просмотра
1
решение |
Записать новую задачу
Все задачи
Все темы
Все инженеры
Темы с решениями Точка, прямая линия и плоскость
Решений 398
Задач 346
Точка, прямая линия и плоскость
Решений 398
Задач 346
 Нет подходящей темы
Решений 309
Задач 307
Нет подходящей темы
Решений 309
Задач 307
 Разрезы
Решений 192
Задач 176
Разрезы
Решений 192
Задач 176
 Чертежи деталей
Решений 156
Задач 134
Чертежи деталей
Решений 156
Задач 134
 Взаимное пересечение поверхностей
Решений 154
Задач 130
Взаимное пересечение поверхностей
Решений 154
Задач 130
 Построение аксонометрических изображений
Решений 128
Задач 92
Построение аксонометрических изображений
Решений 128
Задач 92
|



Комментарии