Определить центр тяжести плоской фигуры

Тема задачи: Расчетно Графические Работы

Создано: @nick 16 марта 2019 19:19

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 16 марта 2019 20:05

поставьте оценку:

1 голосов, средний бал: 5.0000

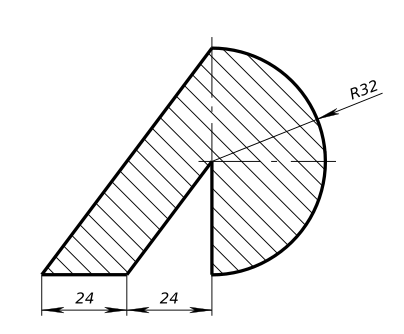
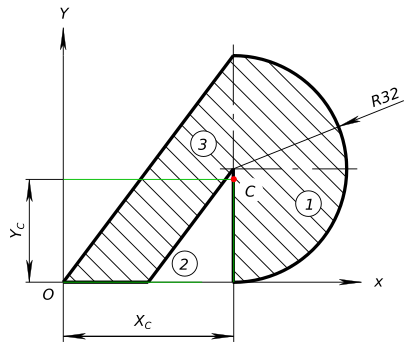
Определить центр тяжести плоской фигуры

Расчетно графическую работу выполняем по следующему алгоритму: - выбираем рациональное направление осей X и Y. Данная плоская фигура не имеет осей симметрии, поэтому ось X проводим по основанию (нижней границе) фигуры и ось Y - по крайней левой точке (границе); - разбиваем сложную фигуру на простые: 1 - полукруг; 2 - треугольник; 3 - треугольник; - определяем координаты их центров тяжести.

1 - полукруг R32

$ X_{C_{1}} = 24+24+\frac{4}{3}\frac{R}{π}=48+\frac{4}{3}×\frac{32}{3,14}=61,58 мм $

$ Y_{C_{1}} = 32 мм $

2 - треугольник

$ X_{C_{2}} = 24+24-\frac{1}{3}×24=40 мм $

$ Y_{C_{2}} =\frac{1}{3}×\frac{R}{1}=\frac{1}{3}×\frac{32}{2}= 10,67 мм $

3 - треугольник

$ X_{C_{3}} = 48 - \frac{1}{3}×(24+24)= 32 мм $

$ Y_{C_{3}} = \frac{1}{3}×2R=\frac{1}{3}×2×32=21,33 мм $

- Определяем площади простых фигур входящих в сложную;

1 - полукруг R32

$ A_{1}=\frac{1}{2}×πR^{2} = \frac{1}{2}×3,14×32×32=1608,50 мм^{2} $

2 - треугольник с катетами 24 мм и 32 мм.

$ A_{2} = \frac{1}{2}(24×32)=384 мм^{2} $

3 - треугольник с катетами 48 мм и 64 мм.

$ A_{3} = \frac{1}{2}((24+24)×2×32)=1536 мм^{2} $

- Определяем координаты центра тяжести плоской фигуры

$ X_{C} = \frac{ΣA_{i}X_{i}}{ΣA_{i}}= $

$ = \frac{1608,50×61,58-384×40+1536×32}{1608,50-384+1536}=48,12 мм $

$ Y_{C} = \frac{ΣA_{i}Y_{i}}{ΣA_{i}}= $

$ = \frac{1608,50×32-384×10,67+1536×21,33}{1608,50-384+1536}=29,03 мм $

- Отмечаем положение центра тяжести фигуры на чертеже.

Определить центр тяжести плоской фигуры

Комментарии

Решения задачи

Комментарии