Все решения инженера @NICKБалка нагруженная моментом
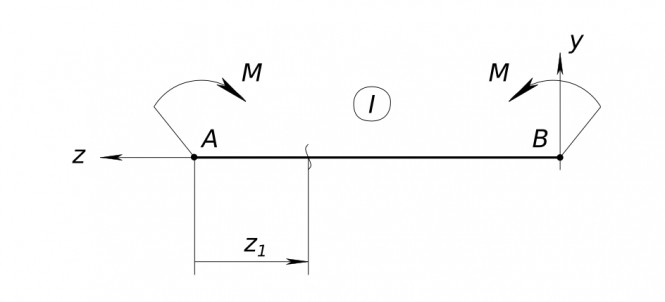
Балка нагруженная моментом Рисуем силовую схему Далее разбиваем стержень на участки. Границами участка служат концы балки. Изменения геометрии сечения балки нет. Получаем один участок - I. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. 
Балка нагруженная моментом Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезаем балку, отбрасываем правую часть. Балка нагруженная моментом
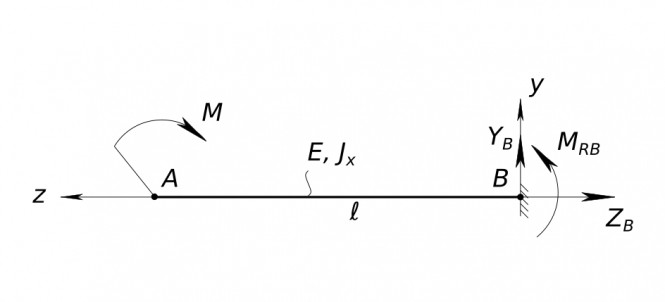
Балка нагруженная моментом Стержневая конструкция все стержни которой лежат в одной плоскости и в этой же плоскости деформируются называется плоской конструкцией. 
Балка нагруженная моментом Для решения задачи вводим систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки моментом: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{B} - горизонтальная реакция Y_{B} - вертикальная реакция M_{RB} - угловая реакция Находим реакции, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю
$ ΣF_{y}=0 $ В сумму входит только Y_{B}. Поэтому, из него находим
$ Y_{B}=0 $ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю.
$ ΣF_{z}=0 $ В сумму входит только Z_{B}. Поэтому, из него находим
$ Z_{B}=0 $ Третье уравнение - сумма всех моментов относительно точки B равна нулю.
$ ΣM_{B}=0 $ Плечи реакций Y_{B} и Z_{B} равны нулю. В сумму входят противоположно направленные M_{RB} и M. Тогда получаем
$ M_{RB}=M $ КомментарииПостроить горизонтальную проекцию точки D ,если она принадлежит плоскости треугольника ABC
Построить горизонтальную проекцию точки D ,если она принадлежит плоскости треугольника ABC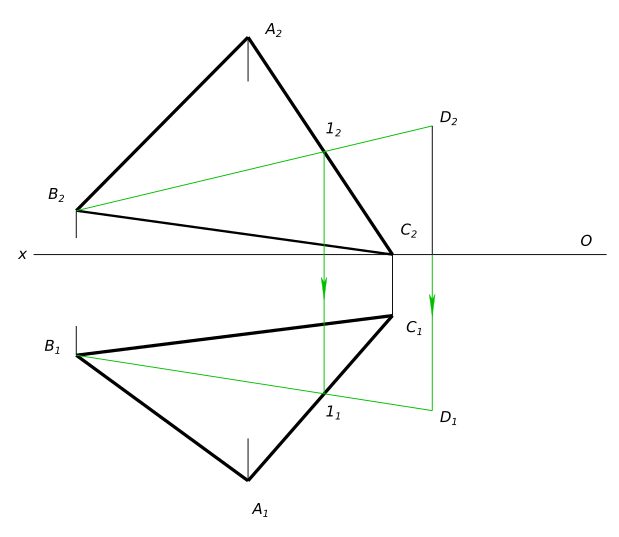 
Построить горизонтальную проекцию точки D ,если она принадлежит плоскости треугольника ABC КомментарииОпределить расстояние между прямыми
Определить расстояние между прямыми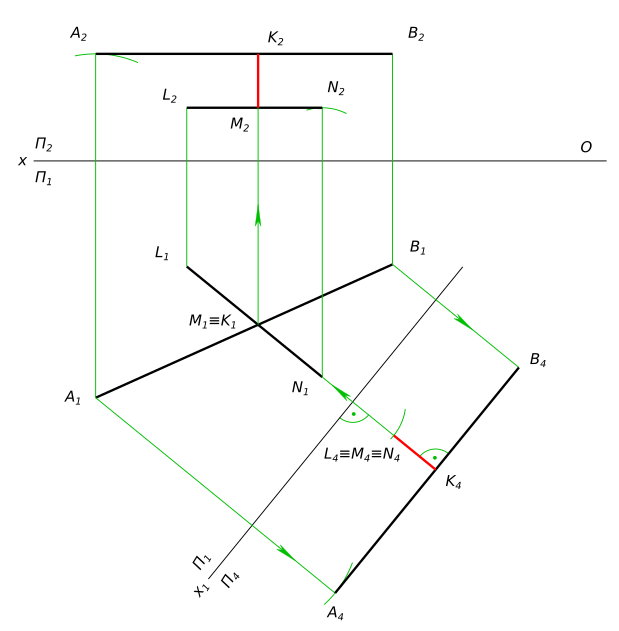 
Определить расстояние между прямыми КомментарииДеталь в терх проекциях
Деталь в трех проекциях 
Деталь в трех проекциях КомментарииПровести плоскость Λ, параллельную плоскости Σ, так чтобы отрезок заданной прямой ...
Провести плоскость Λ, параллельную плоскости Σ, так чтобы отрезок заданной прямой AB, заключенный между плоскостями, имел длину 20 мм. 
Провести плоскость Λ, параллельную плоскости Σ, так чтобы отрезок заданной прямой ... КомментарииПланы скоростей и ускорений.
Сделать планы скоростей и ускорений для девятого положения 
Сделать планы скоростей и ускорений для девятого положения КомментарииПланы скоростей и ускорений.
Сделать планы скоростей и ускорений для второго положения 
Сделать планы скоростей и ускорений для второго положения КомментарииПланы скоростей и ускорений.
Сделать планы скоростей и ускорений для второго положения 
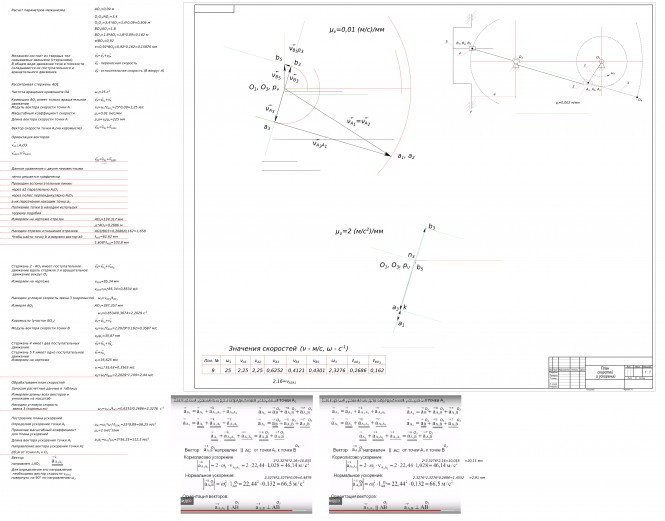
Сделать планы скоростей и ускорений для второго положения КомментарииПривет, увидел ваш закреп, спасибо большое за работу!!!
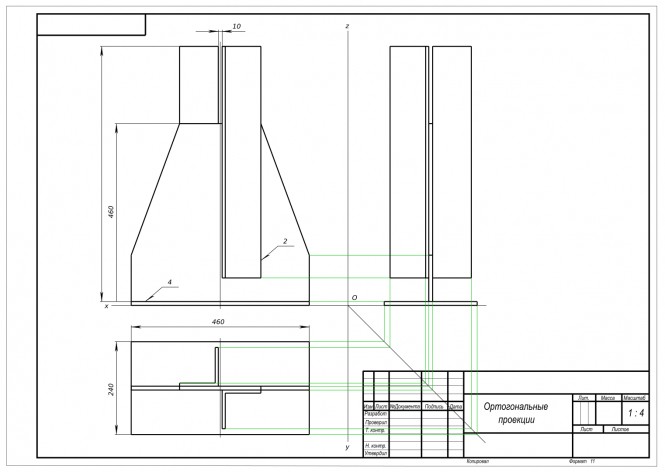
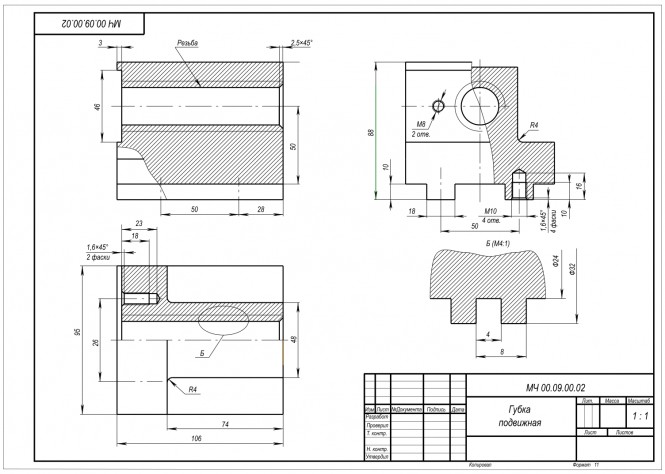
По сборочному чертежу выполнить чертежи деталей
Выполнить чертеж детали поз. 2 
Выполнить чертеж детали поз. 2 КомментарииВариант
Начертить тройник с ввернутой в него справа трубой 
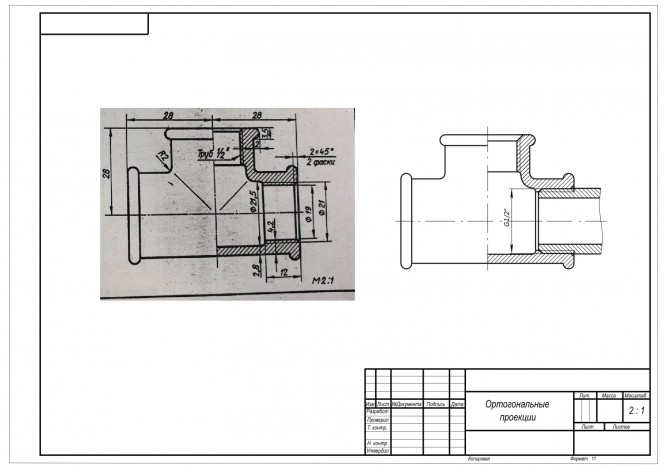
Начертить тройник с ввернутой в него справа трубой Размеры трубы по ГОСТу Внутренний диаметр d=15 мм Наружный D=21,3 мм КомментарииВариант
Начертить деталь А ввернутой в деталь Б 
Начертить деталь А ввернутой в деталь Б КомментарииВариант
Начертить соединение двух деталей шпилькой 
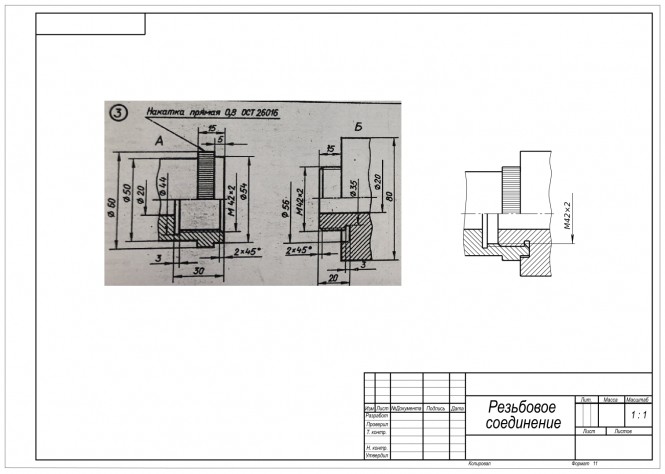
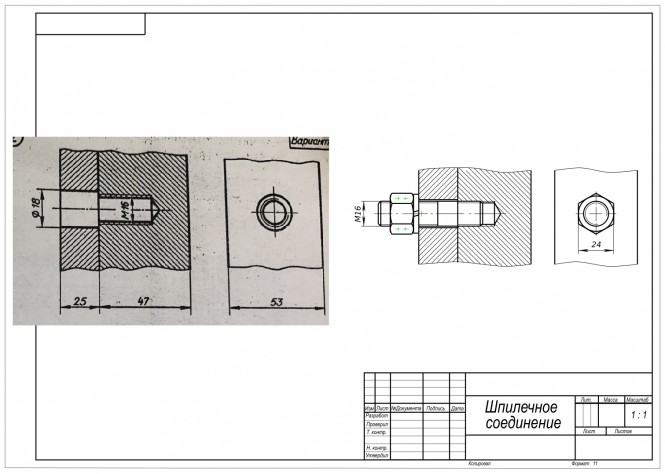
Начертить соединение двух деталей шпилькой Для выполнения задания воспользуемся ГОСТом 22032-76 шпильки с ввинчиваемым концом длиной 1d, в котором определена их конструкция и размеры: Диаметр описанной окружности e=33 мм; Длина резьбы гаечного конца b=38 мм; Длина шпильки ℓ=50 мм; Диаметр стержня d1=16 мм; Номинальный диаметр резьбы 16 мм Шаг резьбы P=2,0 мм; и другие. Используем также ГОСТы на пружинную шайбу, на гайку шестигранную и на сбеги недорезы резьбы. КомментарииВариант
Начертить соединение двух деталей болтом 
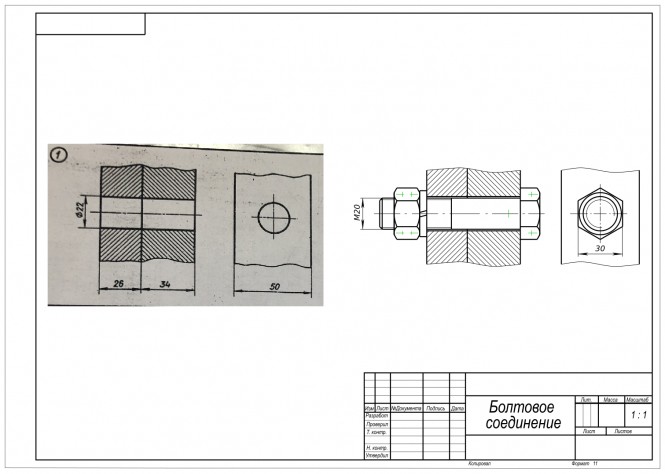
Начертить соединение двух деталей болтом Для выполнения задания воспользуемся ГОСТом 7798-70 Блоты с шестигранной головкой в котором определена их конструкция и размеры: Диаметр описанной окружности e=33 мм; Длина резьбы b=46 мм; Длина болта L=90 мм; Диаметр стержня d1=20 мм; Шаг резьбы P=2,5 мм; Размер «под ключ» S=30 мм; Высота головки k=12,5 мм и другие. КомментарииА остальные задания?
Планы скоростей и ускорений.
Сделать планы скоростей и ускорений для девятого положения 
Сделать планы скоростей и ускорений для девятого положения КомментарииЗдравствуйте nick, сегодня будут планы ускорений?
Я работаю над этим вопросом, но пока еще трудно получается. Не могу ничего обещать.
То есть ещё остался план для 2го положения?
Планы скоростей готовы, остались планы ускорений
Добрый день! А почему на втором чертеже два плана?
Ещё остался план ускорения для второго положения?
Nick, добрый день, А когда ускорения будут готовы?
А на этом чертеже план скоростей и ускорений для 9го?
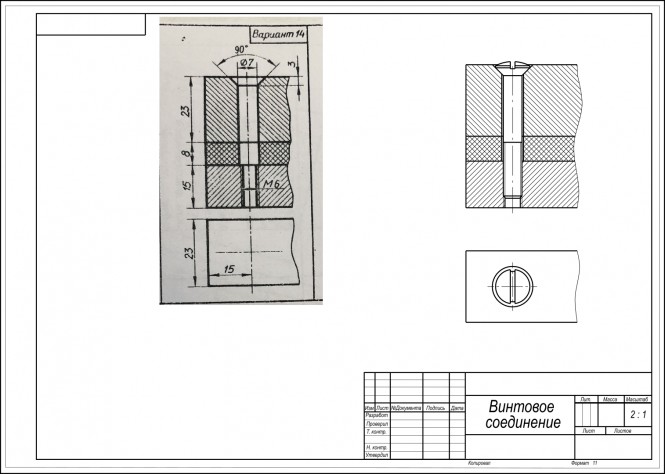
Начертить соединение деталей винтом с полупотайной головкой.14 вариант
Начертить соединение деталей 14 вариант 
Начертить соединение деталей 14 вариант Для выполнения задания воспользуемся ГОСТом 17474-80 Винты с полупотайной головкой в котором определена их конструкция и размеры: Диаметр головки D=11 мм; Длина резьбы b=18 мм; Длина винта ℓ=42 мм; Радиус сферы R1=12 мм и другие. КомментарииЯ оплачу, моё задание решите?
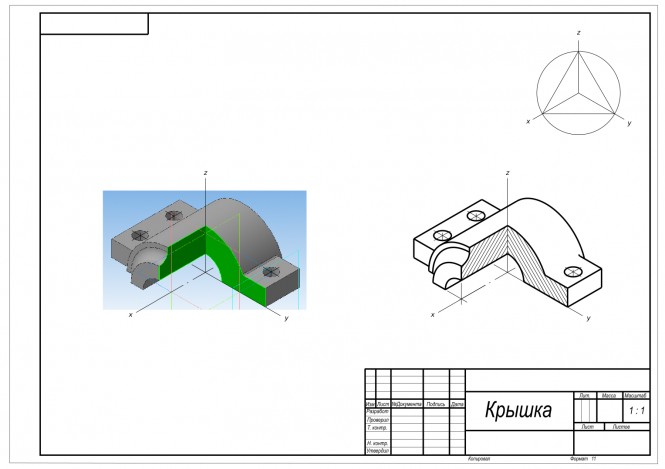
По сборочному чертежу выполнить чертежи деталей
Изометрия детали поз. 5 с вырезом 1/4 части 
Изометрия детали поз. 5 с вырезом 1/4 части КомментарииПостроить плоскость, параллельную плоскости, заданной треугольником ABC, и отстоящую от нее на 35 мм
Построить плоскость, параллельную плоскости, заданным треугольником ABC, и отстоящую от нее на 35 мм A(25;70;58)B(140;42;95)C(90;5;18)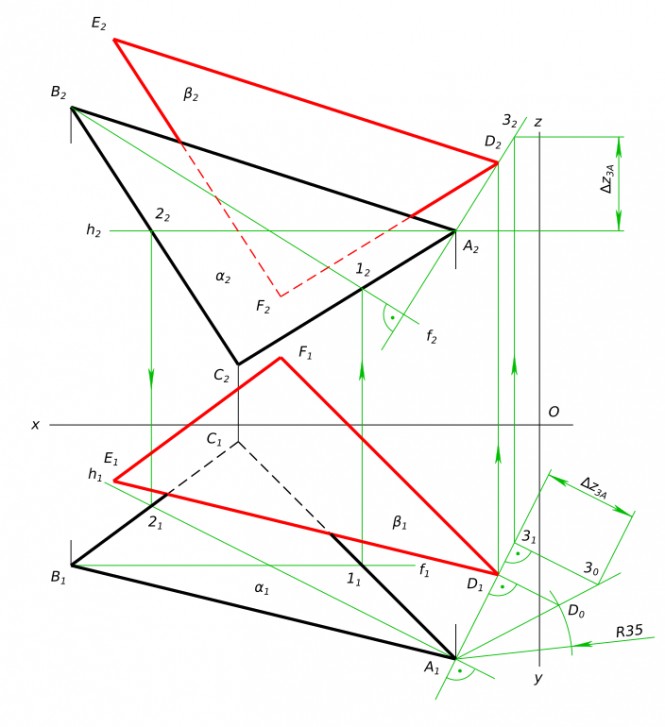 
Построить плоскость, параллельную плоскости, заданной треугольником ABC, и отстоящую от нее на 35 мм A(25;70;58)B(140;42;95)C(90;5;18) КомментарииПостроить линию l пересечения плоскости
Построить линию l пересечения плоскости Δ с плоскостью Ψ (А35 аз.пад. 140° α32°)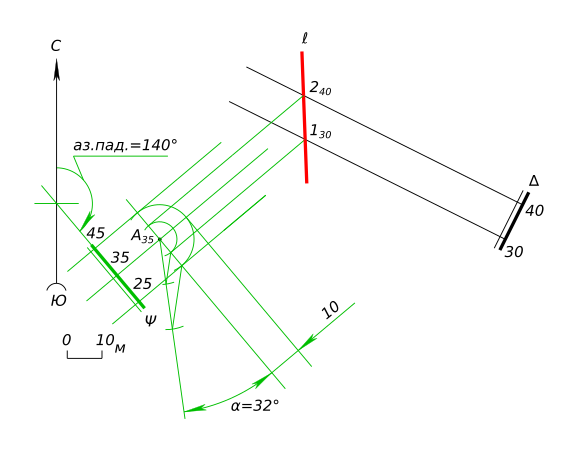 
Построить линию l пересечения плоскости Δ с плоскостью Ψ (А35 аз.пад. 140° 32°) КомментарииПо аксонометрическому изображению детали на формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1
Прямоугольная изометрическая проекция с четвертным вырезом 
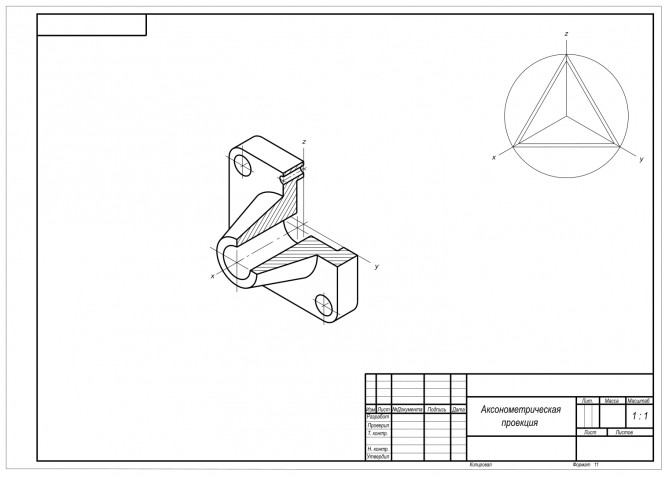
Прямоугольная изометрическая проекция с четвертным вырезом КомментарииПо аксонометрическому изображению детали на формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1
На формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1. Проставить размеры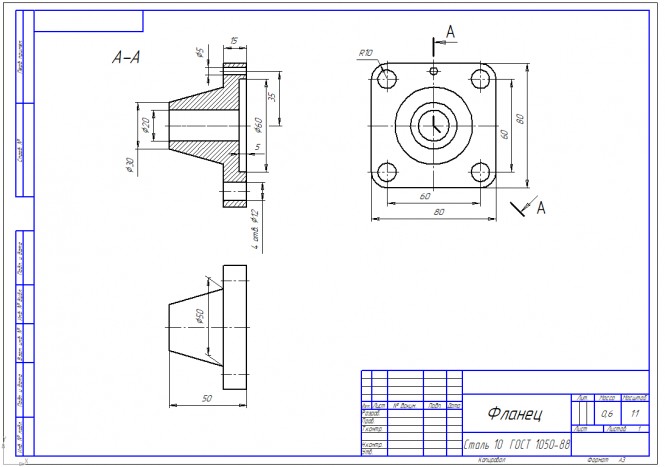 
На формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1. Проставить размеры КомментарииПо аксонометрическому изображению детали на формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1
По аксонометрическому изображению детали на формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1. Проставить размеры.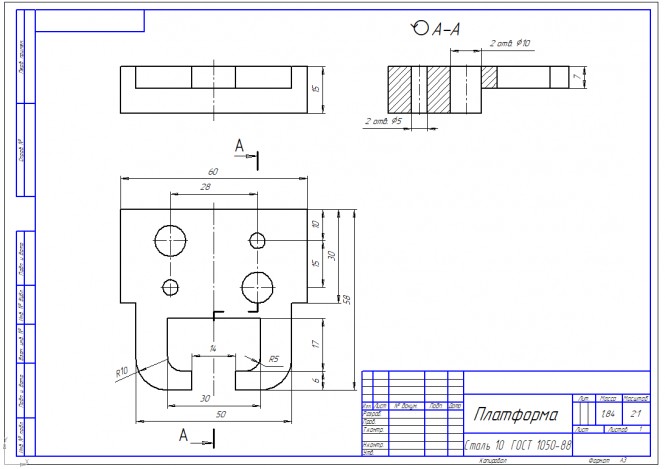 
По аксонометрическому изображению детали на формате А3 выполнить чертеж детали в трех проекциях с необходимыми разрезами в М 2:1. Проставить размеры. КомментарииОпределить центр тяжести плоской фигуры
Определить центр тяжести плоской фигуры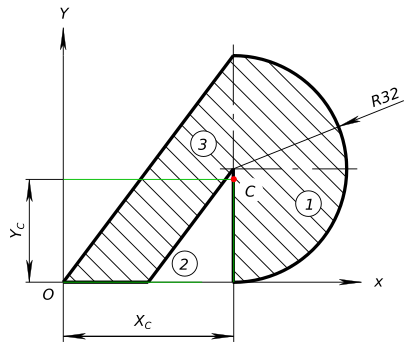 
Определить центр тяжести плоской фигуры Расчетно графическую работу выполняем по следующему алгоритму: - выбираем рациональное направление осей X и Y. Данная плоская фигура не имеет осей симметрии, поэтому ось X проводим по основанию (нижней границе) фигуры и ось Y - по крайней левой точке (границе); - разбиваем сложную фигуру на простые: 1 - полукруг; 2 - треугольник; 3 - треугольник; - определяем координаты их центров тяжести. 1 - полукруг R32
$ X_{C_{1}} = 24+24+\frac{4}{3}\frac{R}{π}=48+\frac{4}{3}×\frac{32}{3,14}=61,58 мм $
$ Y_{C_{1}} = 32 мм $ 2 - треугольник
$ X_{C_{2}} = 24+24-\frac{1}{3}×24=40 мм $
$ Y_{C_{2}} =\frac{1}{3}×\frac{R}{1}=\frac{1}{3}×\frac{32}{2}= 10,67 мм $ 3 - треугольник
$ X_{C_{3}} = 48 - \frac{1}{3}×(24+24)= 32 мм $
$ Y_{C_{3}} = \frac{1}{3}×2R=\frac{1}{3}×2×32=21,33 мм $ - Определяем площади простых фигур входящих в сложную; 1 - полукруг R32
$ A_{1}=\frac{1}{2}×πR^{2} = \frac{1}{2}×3,14×32×32=1608,50 мм^{2} $ 2 - треугольник с катетами 24 мм и 32 мм.
$ A_{2} = \frac{1}{2}(24×32)=384 мм^{2} $ 3 - треугольник с катетами 48 мм и 64 мм.
$ A_{3} = \frac{1}{2}((24+24)×2×32)=1536 мм^{2} $ - Определяем координаты центра тяжести плоской фигуры
$ X_{C} = \frac{ΣA_{i}X_{i}}{ΣA_{i}}= $
$ = \frac{1608,50×61,58-384×40+1536×32}{1608,50-384+1536}=48,12 мм $
$ Y_{C} = \frac{ΣA_{i}Y_{i}}{ΣA_{i}}= $
$ = \frac{1608,50×32-384×10,67+1536×21,33}{1608,50-384+1536}=29,03 мм $ - Отмечаем положение центра тяжести фигуры на чертеже. КомментарииОпустить перпендикуляр из точки D на плоскость ∆ ABC, определить точку K пересечения перпендикуляра с плоскостью ∆ ABC и видимость его на каждой из проекций по конкурирующим точкам. Эпюр 1. Задача А
Опустить перпендикуляр из точки D на плоскость ∆ ABC, определить точку K пересечения перпендикуляра с плоскостью ∆ ABC и видимость его на каждой из проекций по конкурирующим точкам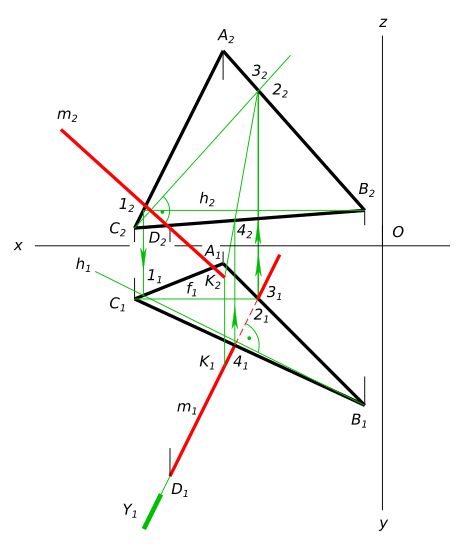 
Опустить перпендикуляр из точки D на плоскость ∆ ABC КомментарииПостроить треугольник ABC найти [BC] и альфа равный BCH
AB=75 AC=80 (.)B принадлежит l AD (.)C принадлежит m AK A 170 60 45 D 50 20 90 K 40 70 45. Построить треугольник ABC найти [BC] и альфа равный BCH. ![Построить треугольник ABC найти [BC] и альфа равный BCH](http://imgsolves.fxyz.ru/1892/solve-image-1.png)
Построить треугольник ABC найти [BC] и альфа равный BCH КомментарииЧерез вершину треугольника ABC и точку M не принадлежащей ABC проведите плоскость β
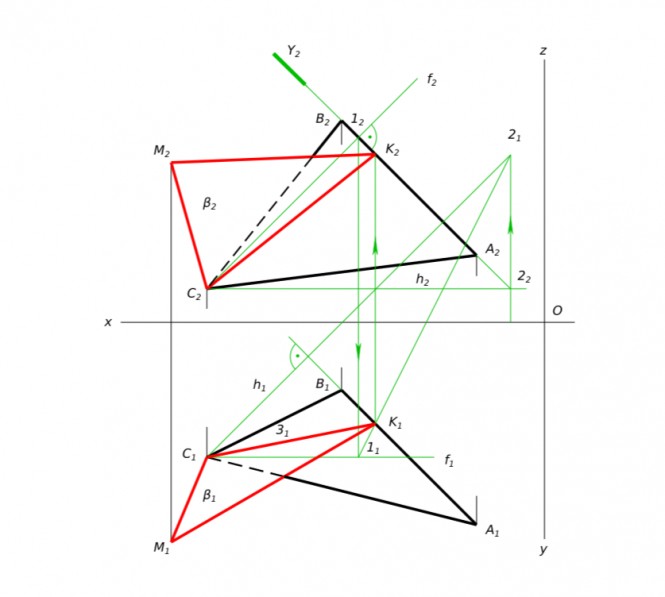
Через вершину треугольника ABC и точку M не принадлежащей ABC проведите плоскость β так, чтобы линия пересечения плоскостей ABC и β была перпендикулярна прямой AB. Координаты точек А (20,60,20); В (60,20,60); С (100,40,10); M(110,65,45) 
Через вершину треугольника ABC и точку M не принадлежащей ABC проведите плоскость β КомментарииПостроить перспективу равностороннего треугольника со сторонами в предметной плоскости.
Отрезок AB произвольного направления принадлежит предметной плоскости. Построить перспективу равностороннего треугольника со сторонами в предметной плоскости.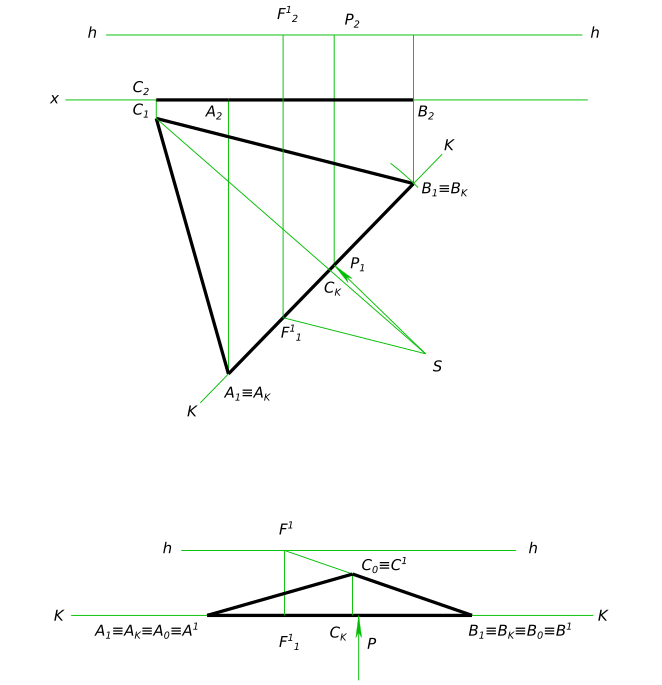 
Построить перспективу равностороннего треугольника со сторонами в предметной плоскости. КомментарииВыполнить расчет фермы
Продолжение расчета фермы Узел F:
$ ΣY = N_{16}sinα+N_{19}sinα-G_{F}=0 $
$ N_{19} = \frac{G_{F}}{sinα}-N_{16}= $
$ =\frac{130+87,5}{0,866}-43,9=207,3 кН $
$ ΣX = -N_{12}-N_{16}cosα+N_{19}cosα+N_{18}=0 $
$ N_{18} = N_{12}+(N_{16}-N_{19})cosα= $
$ =468,2+(43,9-207,3)0,5=386,5 кН $ Узел N:
$ ΣY =-N_{19}sinα-N_{22}sinα=0 $
$ N_{22} =-N_{19}=-207,3 ⇔ 207,3 кН $
$ ΣX =N_{20}-N_{19}cosα-N_{22}cosα+N_{21}=0 $
$ N_{21} =(N_{19}+N_{22})cosα-N_{20}= $
$ =(207,3+207,3)0,5-596,5=-389,2 ⇔ 389,2 кН $ Узел Q:
$ ΣY = -N_{23}=0 $
$ N_{23} =0 $
$ ΣX=N_{21}+N_{26}=0 $
$ N_{26}=-N_{21}=-389,2 ⇔ 389,2 кН $ Узел Q:
$ ΣY = N_{25}sinα-N_{22}sinα-G_{H}=0 $
$ N_{25} = \frac{G_{H}}{sinα}+N_{22}= $
$ = \frac{157,5}{0,866}+207,3=389,2 кН $
$ ΣY =N_{24}+N_{25}cosα+N_{22}cosα-N_{18}=0 $
$ N_{24} =N_{18}-(N_{25}+N_{22})cosα= $
$ =386,5-(389,2+207,3)0,5=88,3 кН $ 
Расчет фермы Узел P:
$ ΣY =-N_{25}sinα-N_{27}sinα=0 $
$ N_{27} =-N_{25}=-389,2 ⇔ 389,2 кН $ Узел M:
$ ΣY =R_{M}-G_{M}-N_{27}sinα=0 $
$ R_{M}=G_{M}+N_{27}sinα= $
$ 43,75+389,2×0,866=380,75 кН $ КомментарииВыполнить расчет фермы
Узел G;
$ ΣY=N_{7}sinα-N_{10}sinα= 0 $
$ N_{10}=N_{7} = 225,8 кН $
$ ΣX=N_{8}+N_{9}+N_{10}cosα+N_{7}cosα= 0 $
$ N_{9} =-(N_{7}+N_{10})cosα-N_{8} $
$ =-(225,8+225,8)0,5-326,8=-552,6 ⇔ 552,6 кН $ Узел D:
$ ΣY =N_{10}sinα+N_{13}sinα-G_{3}= 0 $
$ N_{13} = \frac{G_{3}}{sinα}-N_{10}= $
$ \frac{157,5}}{0,866}-225,8=-43,9 ⇔ 43,9 кН $
$ ΣX =N_{12}-N_{13}cosα-N_{10}cosα-N_{6}=0 $
$ N_{12} = (N_{13}+N_{10})cosα+N_{6}= $
$ (43,9+225,8)0,5+333,3=468,2 кН $ Узел J:
$ ΣY = 0 $
$ N_{5} = 0 $
$ ΣY = N_{9}+N_{14}= 0 $
$ N_{14} = -N_{9}=-552,6 ⇔ 552,6 кН $ Узел K:
$ ΣY=N_{13}sinα-N_{16}sinα=0 $
$ N_{16} = N_{13}=43,9 кН $
$ ΣX=N_{13}cosα+N_{16}cosα+N_{14}+N_{15}=0 $
$ N_{15} = -(N_{13}+N_{16})cosα-N_{14}= $
$ = -(43,9+43,9)0,5-552,6=-596,5 ⇔ 596,5 кН $ 
Расчет фермы Узел L:
$ ΣY = 0 $
$ N_{17} = 0 $
$ ΣY = N_{15}+N_{20}=0 $
$ N_{20} = -N_{15}=-596,5 ⇔ 596,5 кН $ КомментарииВыполнить расчет фермы
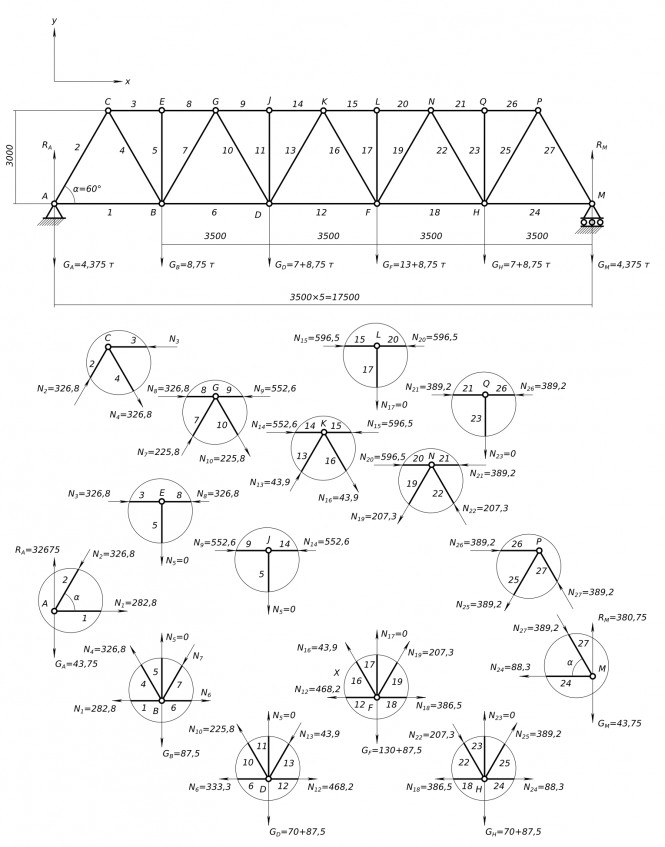
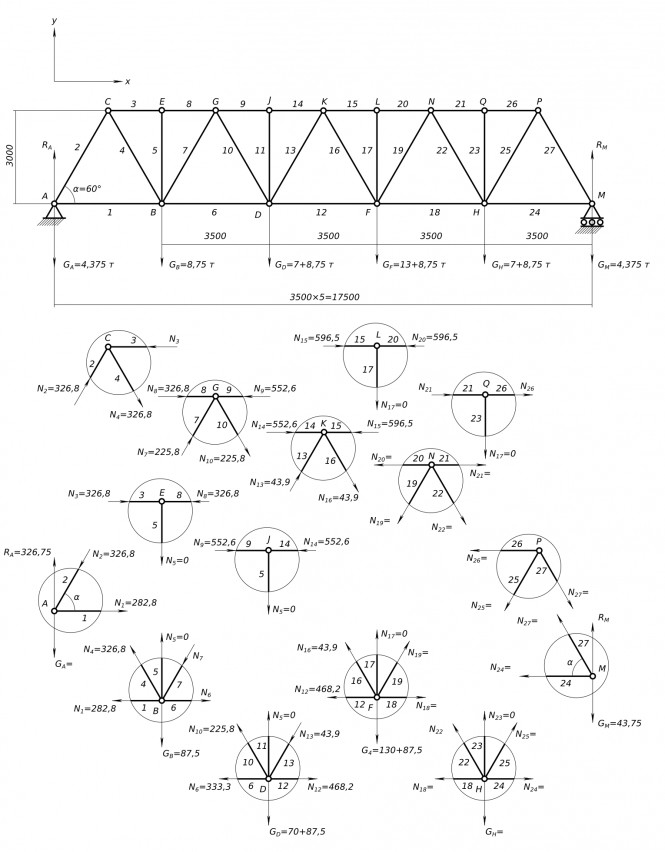
Выполнить расчет фермы для автомобильного и пешеходного мостового перехода 
расчет фермы Определяемся с геометрией и Составляем расчетную схему: - линии стержней проходят через центр тяжести элементов обозначаем цифрами; - узлы обозначаем заглавными латинскими буквами; длина фермы 3500×5=17500; высота фермы - расстояние между верхним и нижним поясом равна 3000; угол α=60°. Собираем нагрузки и правильно их прикладываем: - дорожное полотно дает распределенную по длине моста нагрузку q=2,5 т/м - Трехосный грузовой автомобиль с полной нагрузкой массой 33,5 т, в т. ч. на переднюю ось 7,5 т, в т. ч. на заднюю тележку 26 т. Расстояние между осями 4 м. Расчет фермы выполняем согласно принятой схемы наиболее опасного нагружения в процессе эксплуатации. Ферма - плоская шарнирно-стержневая система. По умолчанию считается что ферма является статически определимой и геометрически не изменяемой системой. Все узлы принимаются шарнирными без этого не получится статически определяемая система. Замена жестких узлов шарнирами превращает их в шарнирную ферму. При узловой нагрузке стержни шарнирной фермы работают на растяжение или сжатие. Расчет фермы начинается с определения опорных реакций: - имеем вертикальные составляющие RA и RM; - горизонтальные составляющие отсутствуют так как все нагрузки вертикальны. Для плоской системы составляем условия равновесия: - проекция всех сил на ось Х; - проекция всех сил на ось Y; - уравнение моментов относительно какой либо точки.
$ ΣX = 0; $
$ ΣY = R_{A}+R_{M}-G_{1}-G_{2}-G_{3}-G_{4}-G_{5}-G_{6}=0; $
$ ΣM_{A} = 3,5G_{2}+7G_{3}+10,5G_{4}+14G_{5}+17,5G_{6}-17,5R_{M}=0 $ Из уравнения моментов находим
$ R_{M} =\frac{3,5G_{2}+7G_{3}+10,5G_{4}+14G_{5}+17,5G_{6}}{17,5} = $
$ =380,75 кН $ Тогда
$ R_{A}=G_{1}+G_{2}+G_{3}+G_{4}+G_{5}+G_{6}-R_{M}= $
$ =43,75+87,5+157,5+217,5+157,5+43,75-380,75= $
$ = 326,75 кН $ Метод вырезания узлов используем для определения усилий в стержнях фермы: - неизвестные усилия первоначально принимаем растягивающими (стрелка характеризующая вектор силы направлена от узла); - если найденное значение силы со знаком минус, то это означает что стержень работает не на растяжение а на сжатие. В этом случае меняем направление вектора силы на противоположное направленное к узлу. Узел A
$ ΣY = R_{A}-G_{1}+N_{2}sinα=0 $
$ N_{2}=\frac{G_{1}-R_{A}}{sinα}=\frac{43,75-326,75}{0,866}=-326,8 кН ⇔ 326,8 кН $
$ ΣX = N_{1}-N_{2}cosα=0 $
$ N_{1}=N_{2}cosα=326,8×0,5=163,4 кН $ Узел C:
$ ΣY = N_{2}sinα-N_{4}sinα=0 $
$ N_{4}=\frac{N_{2}sinα}{sinα}=N_{2}=326,8 кН $
$ ΣX =N_{2}cosα+N_{4}cosα+N_{3}=0 $
$ N_{3}=-(N_{4}+N_{2})cosα==-326,8 ⇔ 326,8 кН $ Узел E;
$ ΣY = N_{5}=0 $
$ ΣX = N_{3}+N_{8}=0 $
$ N_{8}=-N_{3}=-326,8 ⇔ 326,8 кН $ Узел B:
$ ΣY = N_{7}sinα+N_{4}sinα-G_{2}=0 $
$ N_{7} = \frac{G_{2}-N_{4}sinα}{sinα}= $
$ = \frac{87,5-326,8×0,866}{0,866}=-225,8 ⇔ 225,8 кН $
$ ΣX = N_{6}-N_{1}+N_{7}cosα-N_{4}cosα=0 $
$ N_{6} = N_{1}+(N_{4}-N_{7})cosα= $
$ = 282,8+(326,8-225,8)0,5=333,3 кН $ Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии