Все решения инженера @NICKПостроить эпюры продольных сил и нормальных напряжений по длине бруса
Двух ступенчатый стальной брус нагружен силами: F1=20 кН; F2=10 кН; F3=5 кН. Площади поперечных сечений бруса: A1=1,8 см2; A2=3,2 см2. a=0,2 м. Принять E=2х100000 МПа, [σ]=160 МПа. Построить эпюры продольных сил, нормальных напряжений. Определить перемещение конца бруса. 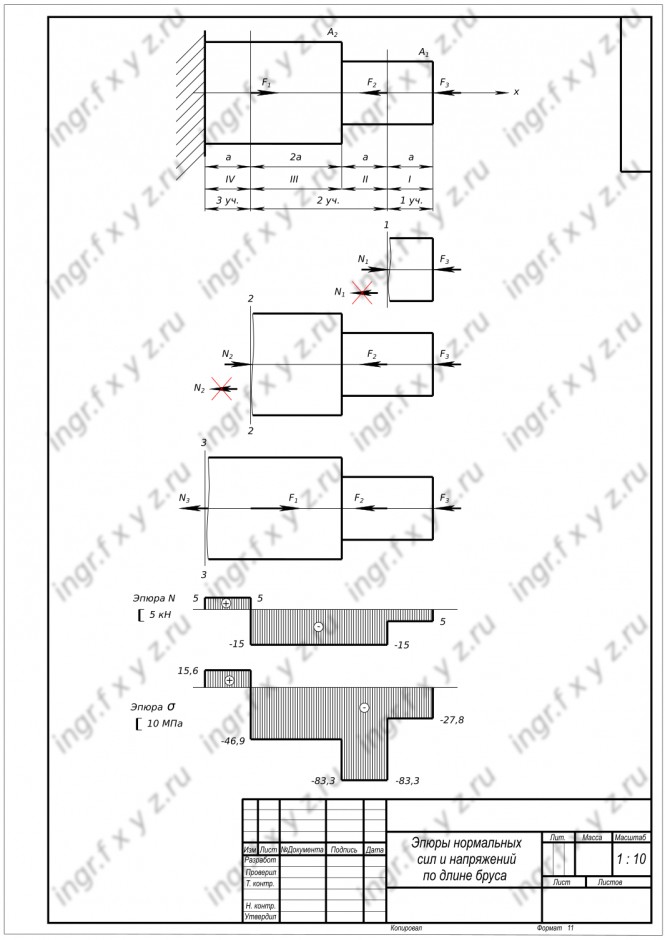
Двух ступенчатый стальной брус нагружен силами: F1=20 кН; F2=10 кН; F3=5 кН. Площади поперечных сечений бруса: A1=1,8 см2; A2=3,2 см2. a=0,2 м. Принять E=2х100000 Н/мм2. Построить эпюры нормальных сил и напряжений по длине бруса. Определить перемещение конца бруса. Брус закреплен в стене - закрепление заделка. Сечения бруса круглой формы
$ A = \frac{πd^{2}}{4} $ Находим диаметры ступеней бруса.
$ d = \sqrt{\frac{4A}{π}} $
$ d_{1}=15,14 мм; d_{2}=20,19 мм $ Делим брус на участки нагружения (части бруса между внешними силами) - участки 1, 2 и 3. Используем метод сечений для определения внутренних силовых факторов, действующих на каждом участке (при этом внутренние силы переходят в разряд внешних): Участок 1. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-N_{1}=0; N_{1}=-F_{3}= -5 кН $ Продольная сила N1 Знак минус означает, что действительное направление N1 противоположно первоначально выбранному.. Участок 1 сжат. Участок 2. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-F_{2}-N_{2}=0; N_{2}=-F_{3}-F_{2}=-5-10= -15 кН $ Продольная сила N2 отрицательна. Знак минус означает, что действительное направление N2 противоположно первоначально выбранному. Участок 2 сжат. Участок 3. Проецируем силы действующие на участок на ось х и составляем уравнение равновесия
$ ΣF_{x} = 0; -F_{3}-F_{2}+F_{1}-N_{3}=0; N_{3}=20 - 5 -10= 5 кН $ Продольная сила N3 положительна. Это означает, что действительное направление N3 совпадает с первоначально выбранным. Участок 3 растянут. Определяем величины нормальных напряжений по сечениям с учетом изменения площади поперечного сечения. Четыре участка по напряжениям:
$ σ_{1} =\frac{N_{1}}{A_{1}}=\frac{5×10^{3}}{1,8×100}=27,8 \frac{Н}{мм^{2}}=27,8 МПа $
$ σ_{2} =\frac{N_{2}}{A_{1}}=\frac{15×10^{3}}{1,8×100}=83,3 МПа $
$ σ_{3} =\frac{N_{2}}{A_{2}}=\frac{15×10^{3}}{3,2×100}=46,9 МПа $
$ σ_{4} =\frac{N_{3}}{A_{2}}=\frac{5×10^{3}}{3,2×100}=15,6 МПа $ Строим эпюры продольных сил и эпюру нормальных напряжений, полагая растягивающие напряжения положительными. Эпюра продольных сил показывает изменение внутреннего силового фактора по длине бруса: участки I, II и III испытывают деформацию сжатия; участок IV испытывает деформацию растяжения. Эпюра нормальных напряжений показывает их изменение по длине бруса. Наиболее опасным участком является участок II. Так как нормальные напряжения на нем максимальны по величине σII=83,3 МПа Проверяем прочность бруса работающего на растяжение - сжатие: по условию прочности $ |σ_{max}=83,3 МПа|≤[σ=160 МПа] $ Прочность обеспечена. На каждом участке определяем абсолютную деформацию (удлинение или сжатие):
$ ∆ℓ_{1} = \frac{σ_{1}L_{1}}{E}=\frac{-27,8×10^{3}×0,2}{200×10^{3}}=-0,028 мм $
$ ∆ℓ_{2} = \frac{σ_{2}L_{2}}{E}=\frac{-83,3×10^{3}×0,2}{200×10^{3}}=-0,083 мм $
$ ∆ℓ_{3} = \frac{σ_{3}L_{3}}{E}=\frac{-46,9×10^{3}×0,4}{200×10^{3}}=-0,094 мм $
$ ∆ℓ_{4} = \frac{σ_{4}L_{4}}{E}=\frac{15,6×10^{3}×0,2}{200×10^{3}}=0,016 мм $ Суммарное удлинение бруса (перемещение свободного конца)
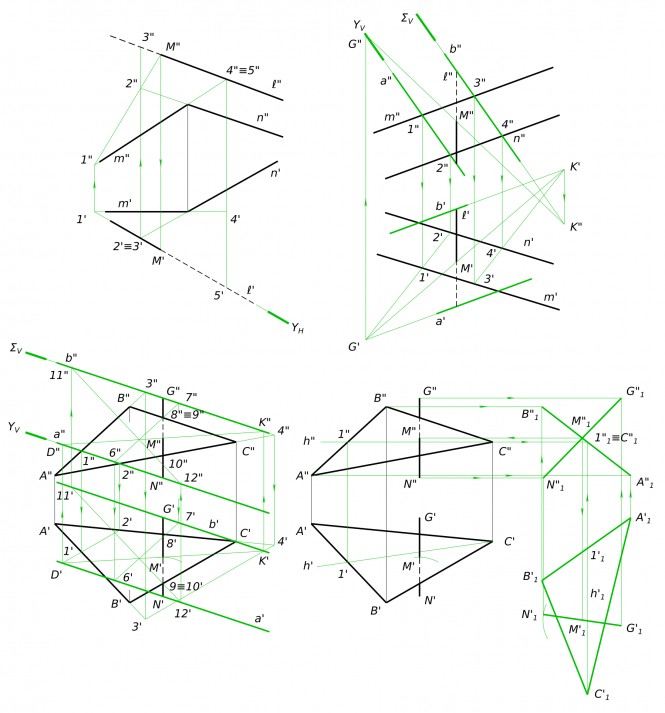
$ ∆ℓ=∆ℓ_{1}+∆ℓ_{2}+∆ℓ_{3}+∆ℓ_{4}=-0,189 мм $ Построить фронтальную проекцию треугольника LMN
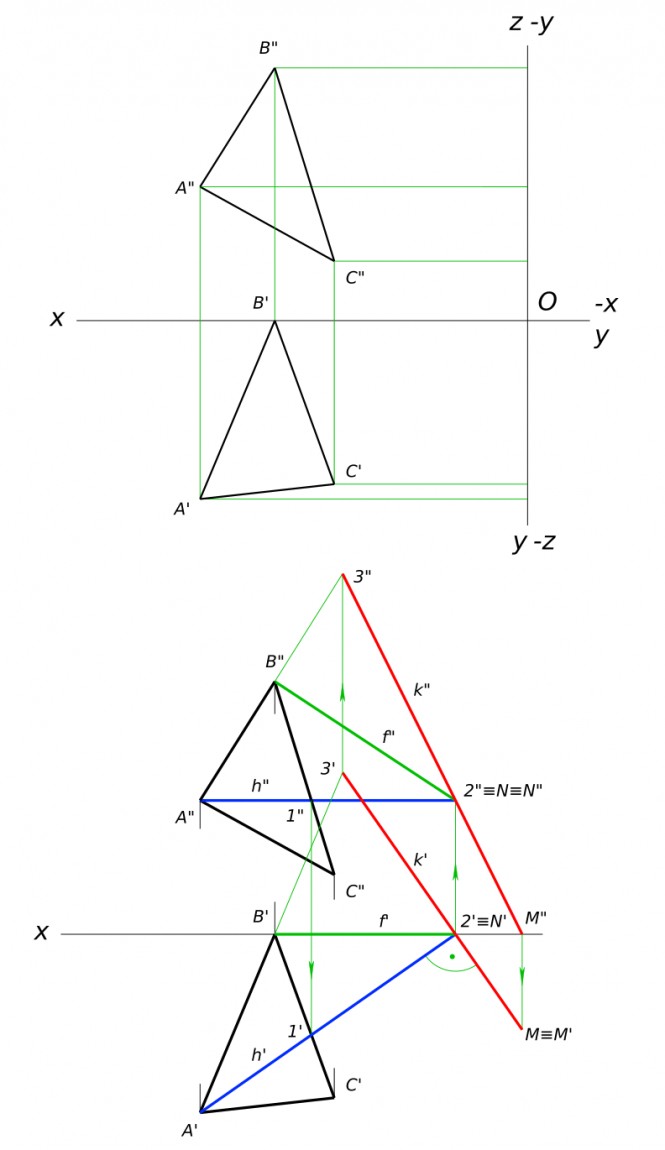
Построить фронтальную проекцию треугольника LMN , если известна горизонталь h и угол наклона плоскости треугольника к П1 равен 30 градусов 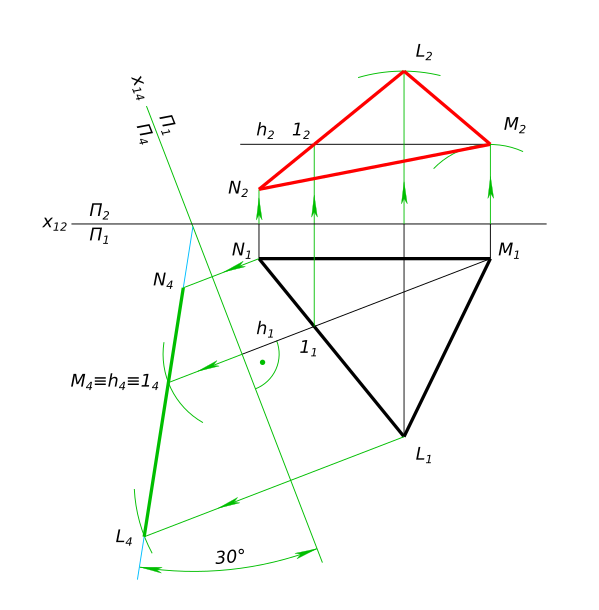
Построить фронтальную проекцию треугольника LMN Построить горизонтальную проекцию треугольника ABC, если его плоскость параллельна плоскости β (k//n)
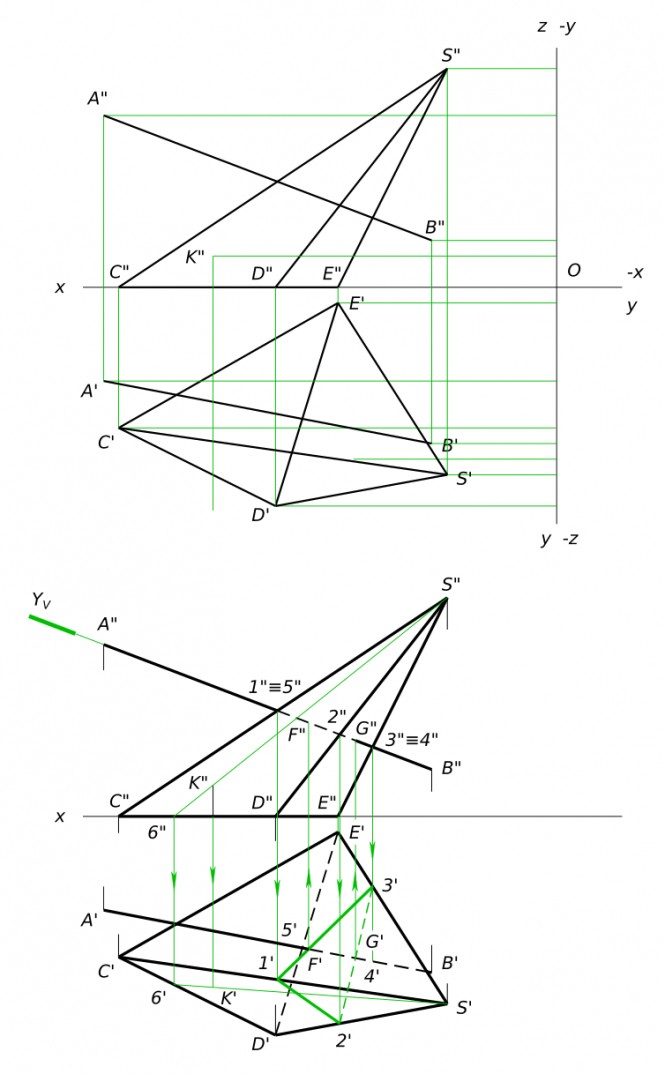
Построить горизонтальную проекцию треугольника ABC(A', ?, ?; A"B"C"), если его плоскость параллельна плоскости β (k//n) 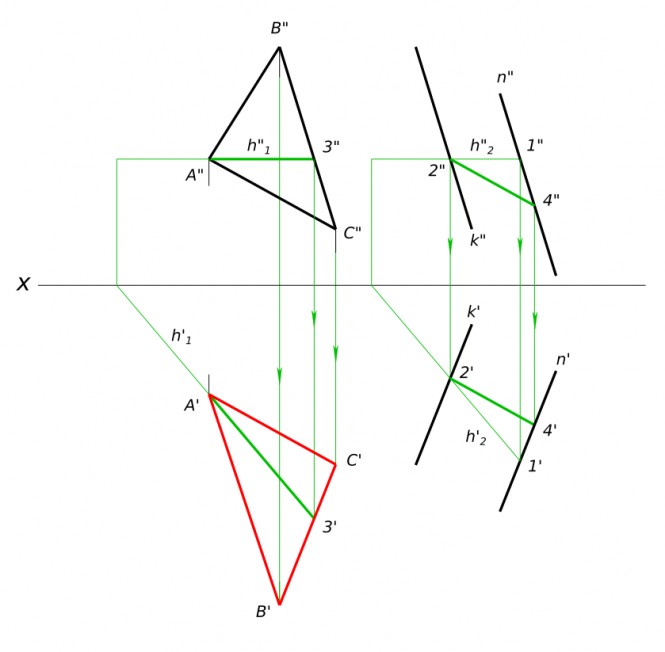
Построить горизонтальную проекцию треугольника ABC(A', ?, ?; A"B"C"), если его плоскость параллельна плоскости β (k//n) КомментарииПостроить третье изображение
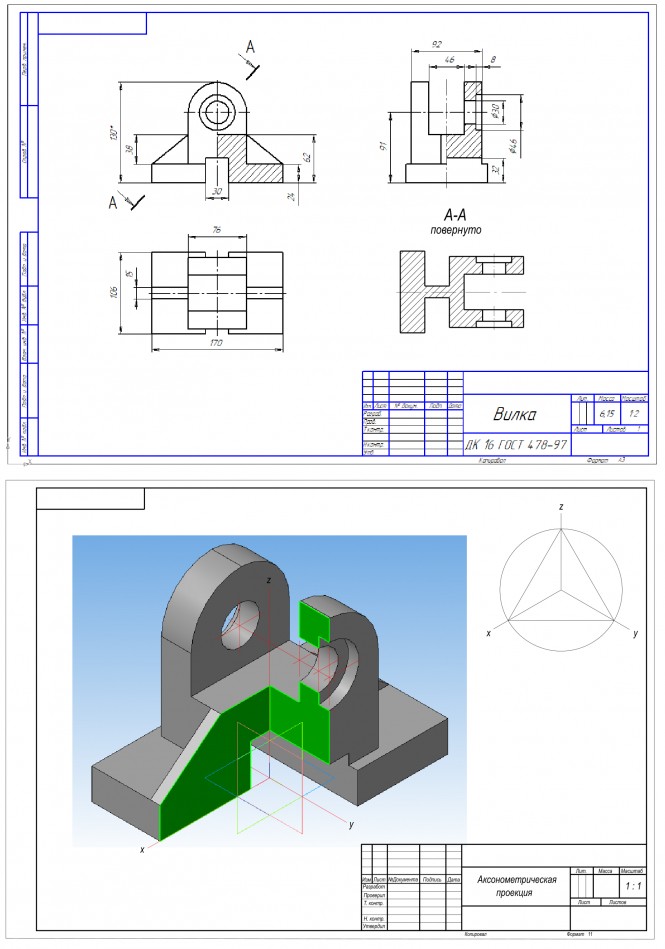
Построить наглядное изображение детали в аксонометрической проекции Комментарии1. Начертить соединение двух деталей болтом. Размеры болта подобрать по ГОСТу. 2. - шпилькой. Размеры шпильки -. 3. - деталь А,
1. Начертить соединение двух деталей болтом. Размеры болта подобрать по ГОСТу. 2. - шпилькой. Размеры шпильки -. 3. - деталь А, 1. Начертить соединение двух деталей болтом. Размеры болта подобрать по ГОСТу. 2. Начертить соединение двух стальных деталей шпилькой. Размеры шпильки подобрать по ГОСТу. 3. Начертить деталь А, навернутой на деталь Б. 4. Начертить угольник прямой с ввернутой в него справа трубой. Размеры трубы подобрать по ГОСТу. 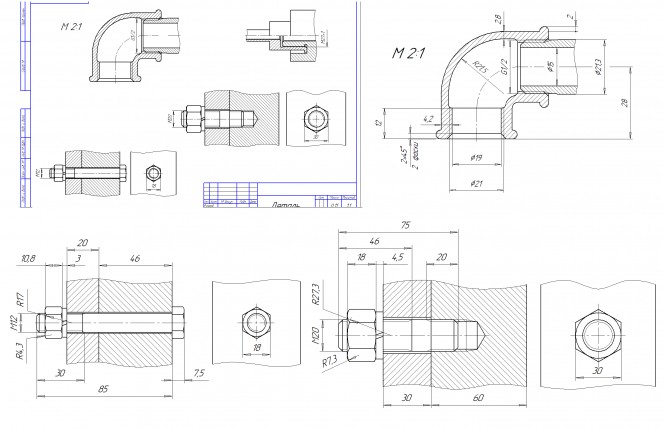
1. Начертить соединение двух деталей болтом. Размеры болта подобрать по ГОСТу. 2. - шпилькой. Размеры шпильки -. 3. - деталь А, Вне поля чертежа показаны размеры деталей резьбового соединения, необходимые для его построения. Конструкция и размеры болта установлены ГОСТ 7798-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры болта: резьба M = 12; шаг 1,75 мм; диаметр стержня d1 = 12 мм; высота головки k = 7,5 мм; диаметр описанной окружности e = 19,9 мм; длину резьбы b = 30 мм. Конструкция и размеры гайки установлены ГОСТ 5915-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры гайки: резьба M = 12; шаг 1,75 мм; размер под ключ S = 18 мм; высота гайки m = 10,8 мм; диаметр описанной окружности e = 19,9 мм. Конструкция и размеры шайбы установлены ГОСТ 6202-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы болта находим необходимые для вычерчивания параметры шайбы: d=12,2 мм; b=s 3 мм; m=0,7s. Конструкция и размеры шпильки установлены ГОСТ 22032-76. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры шпильки: резьба M = 20; шаг 2,5 мм; диаметр стержня d1 = 20 мм; длину резьбы гаечного конца b = 46 мм; длину резьбы ввинчиваемого конца b1 = 20 мм. Конструкция и размеры гайки установлены ГОСТ 5915-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы находим необходимые для вычерчивания параметры гайки: резьба M = 20; шаг 2,5 мм; размер под ключ S = 30 мм; высота гайки m = 18 мм; диаметр описанной окружности e = 33 мм. Конструкция и размеры шайбы установлены ГОСТ 6202-70. Они показаны в его чертежах и таблицах. Здесь по заданному номинальному диаметру резьбы шпильки находим необходимые для вычерчивания параметры шайбы: d=20,5 мм; b=s 4,5 мм; m=0,7s . Также при вычерчивании резьбовых соединений принимаются во внимание: ГОСТ 10549-80. Выход резьбы. Сбеги, недорезы, проточки и фаски; ГОСТ 24705-81 Основные нормы взаимозаменяемости. Резьба метрическая; ГОСТ 6357-73 Резьба трубная цилиндрическая. Для вычерчивания трубы размеры берем по ГОСТ 3262-75 Трубы стальные водогазопроводные. КомментарииНайти центр описанной около треугольника окружности.
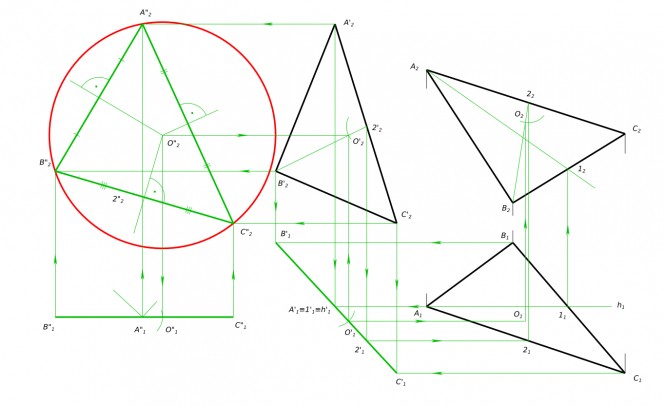
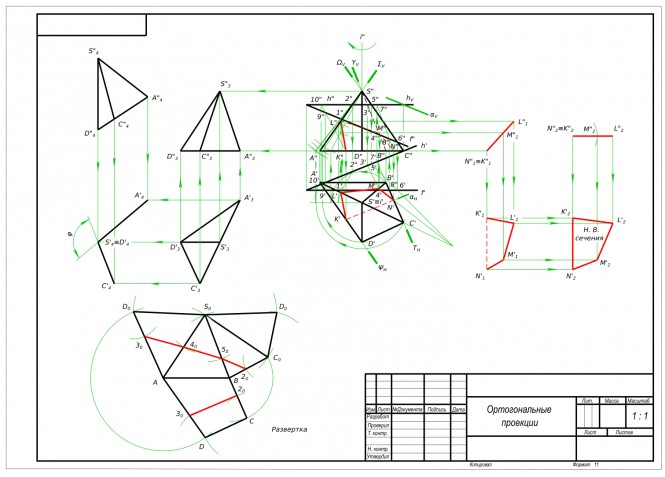
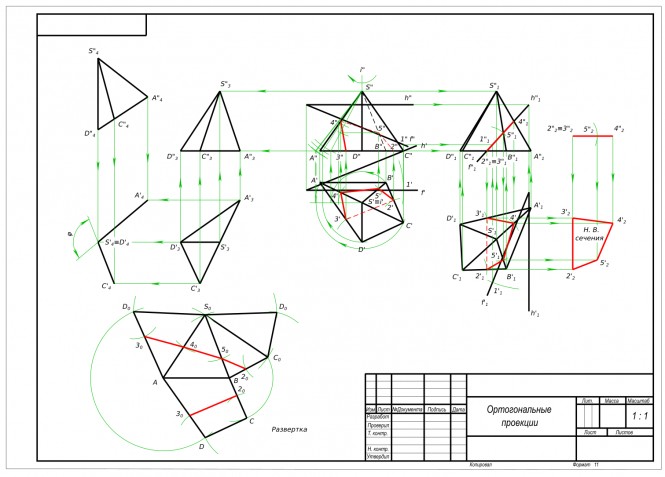
Найти центр описанной около треугольника окружности Чтобы выполнить задание необходимо знать как строится описанная около треугольника окружность. Представим себе ее для этого. Стороны треугольника - хорды окружности. Центр окружности находится на перпендикуляре к хорде, проведенном через ее середину. Построив данные перпендикуляры найдем в их пересечении центр описанной окружности. Предварительно способами преобразования чертежа строим натуральную величину треугольника. КомментарииПо двум проекциям выполнить третью и построить линию пересечения призмы и полусферы
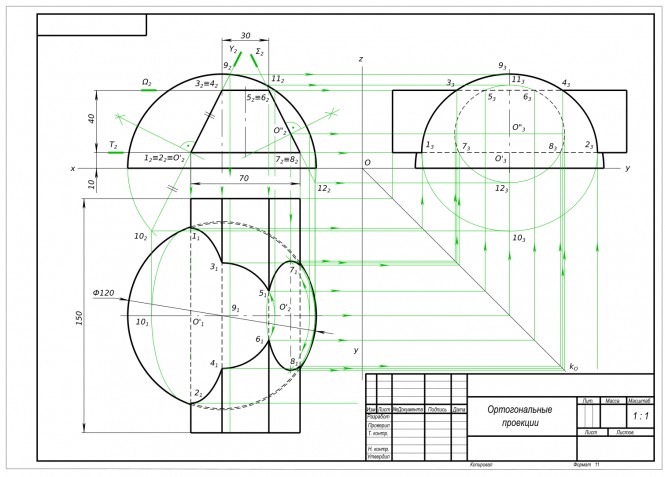
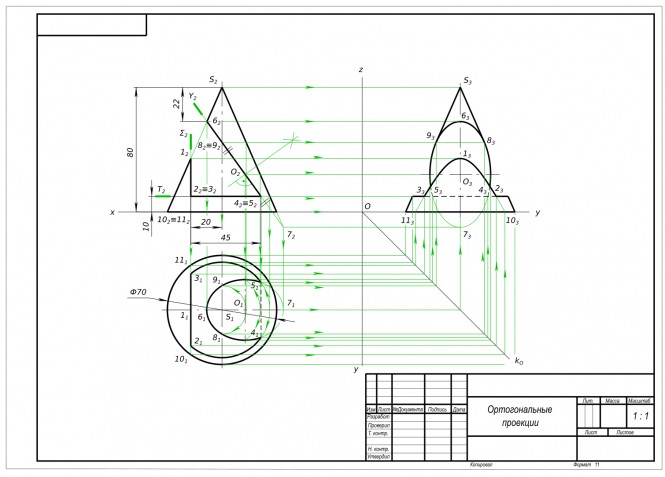
По двум проекциям выполнить третью и построить линию пересечения призмы и полусферы КомментарииПостроить три проекции конуса с вырезом
Построить три проекции конуса с вырезом КомментарииПостроить линию пересечения плоскостей α - A(145; 65; 100), B(90; 110; 100), C(40; 10; 0) и β - D(16; 52; 65), M(140; 115; 20),
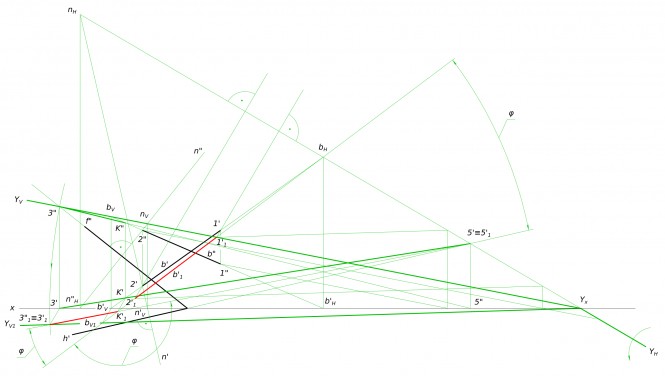
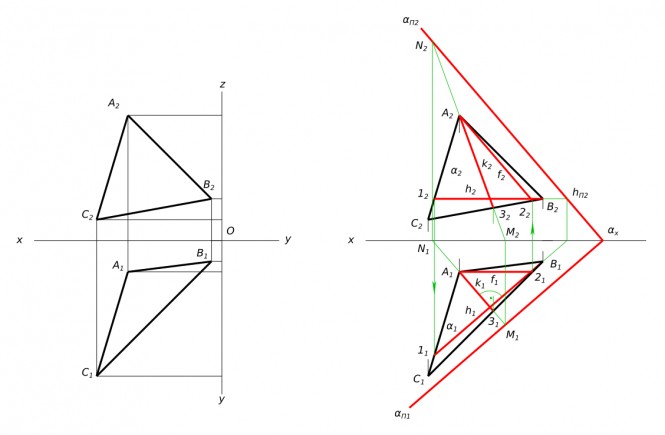
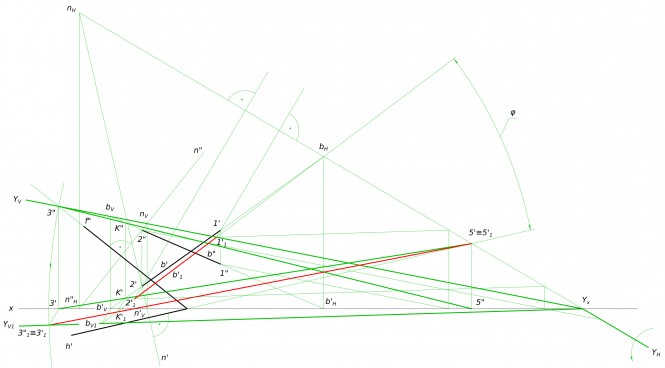
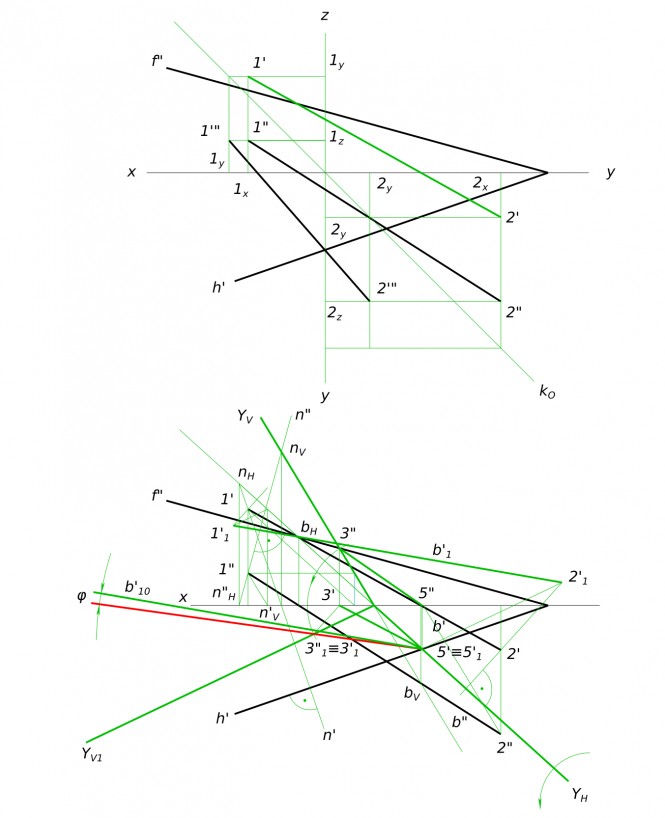
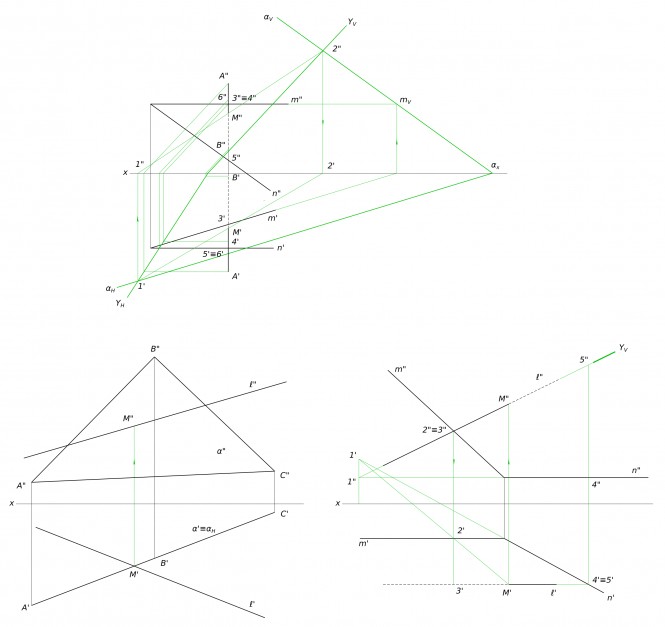
Построить линию пересечения плоскостей α - A(145; 65; 100), B(90; 110; 100), C(40; 10; 0) и β - D(16; 52; 65), M(140; 115; 20), E(102; 17; 93). 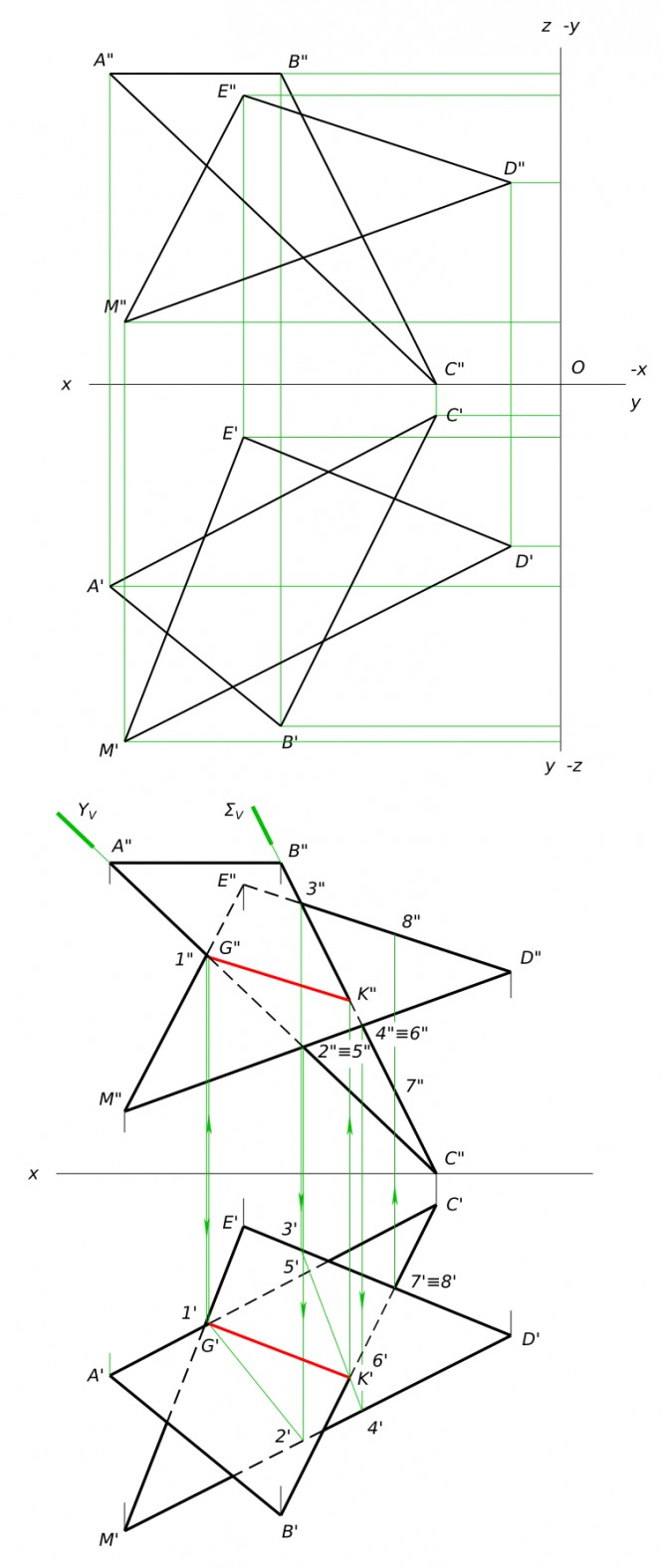
Построить линию пересечения плоскостей α - A(145; 65; 100), B(90; 110; 100), C(40; 10; 0) и β - D(16; 52; 65), M(140; 115; 20), E(102; 17; 93) КомментарииПересечение тела прямой линией
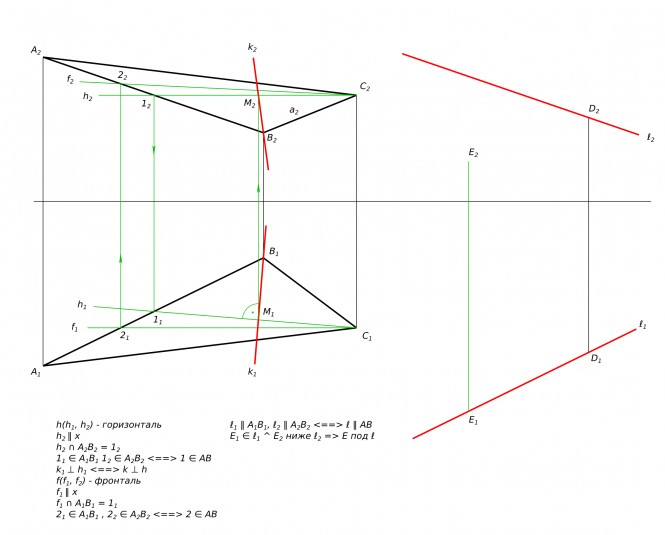
Пересечение тела прямой линией КомментарииОпределить угол между линией и плоскостью
Определить угол между линией и плоскостью КомментарииГлавные линии плоскости
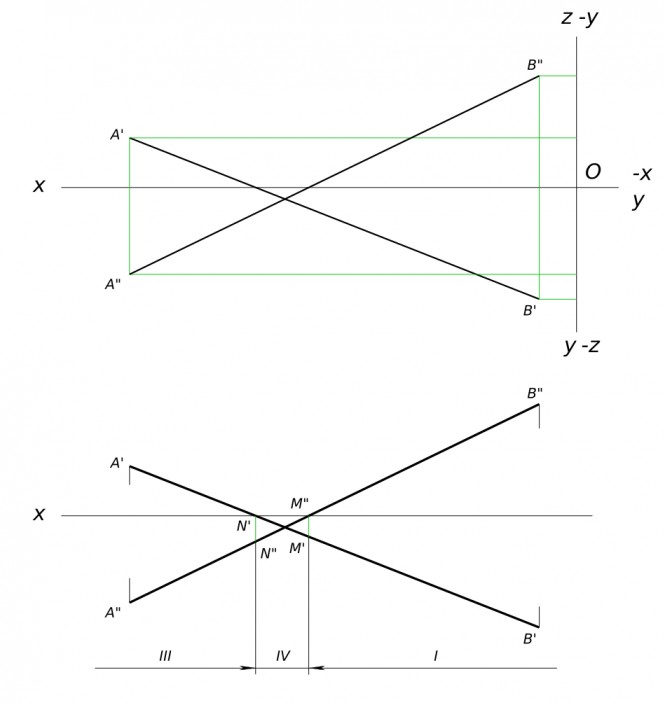
Главные линии плоскости 14 вариант A(110;60;45) B(85;0;85) C(65;55;20) КомментарииПо координатам отрезка AB построить его горизонтальную и фронтальную проекции. Графически показать, через какие четверти пространства прошла прямая AB
По координатам отрезка AB построить его горизонтальную и фронтальную проекции. Графически показать, через какие четверти пространства прошла прямая AB КомментарииПостроить проекции центра окружности радиуса 15 мм лежащей в плоскости а и касательной к ее следам
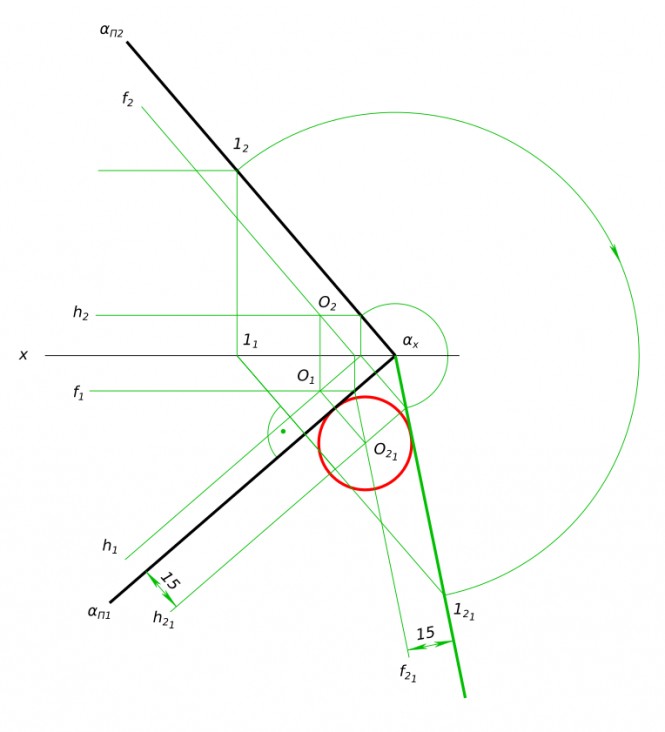
Построить проекции центра окружности радиуса 15 мм лежащей в плоскости а и касательной к ее следам КомментарииПостроить линию пересечения пирамиды с плоскости а также определить видимость фигуры
Построить линию пересечения пирамиды с плоскости а также определить видимость фигуры КомментарииПостроить линию пересечения пирамиды с плоскости а также определить видимость фигуры
Построить линию пересечения пирамиды с плоскости а также определить видимость фигуры КомментарииИзвините, но сечение нужно было сделать другим методом
Можно будет исправить?
Определить угол между линией и плоскостью
Определить угол между линией и плоскостью КомментарииДобрый день, задача решена неверно. Преподаватель указал, что угол должен быть между 1'2'3'. Не могли бы вы показать верное решение?
Построение трех проекций геометрического тела с вырезом
Построение трех проекций геометрического тела с вырезом КомментарииПостроить три проекции детали с совмещёнными разрезами, построить аксонометрию с вырезом четверти детали
Построить три проекции детали с совмещёнными разрезами, построить аксонометрию с вырезом четверти детали 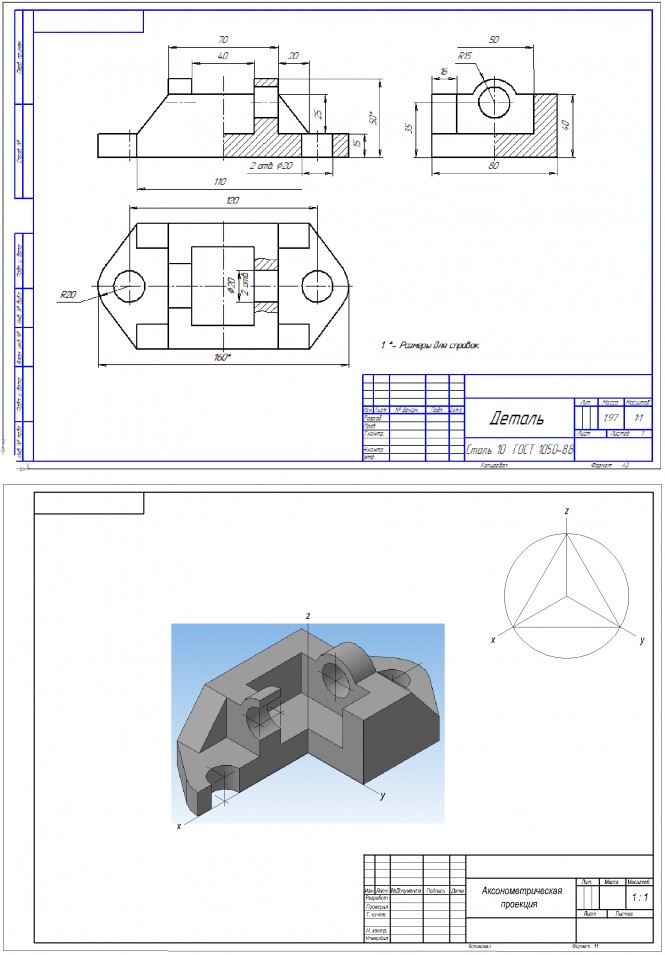
Построить три проекции детали с совмещёнными разрезами, построить аксонометрию с вырезом четверти детали КомментарииПостроить третье изображение
Построить третье изображение детали по двум данным, дать разрезы, построить натуральный вид наклонного сечения, а также наглядное изображение детали в аксонометрической проекции 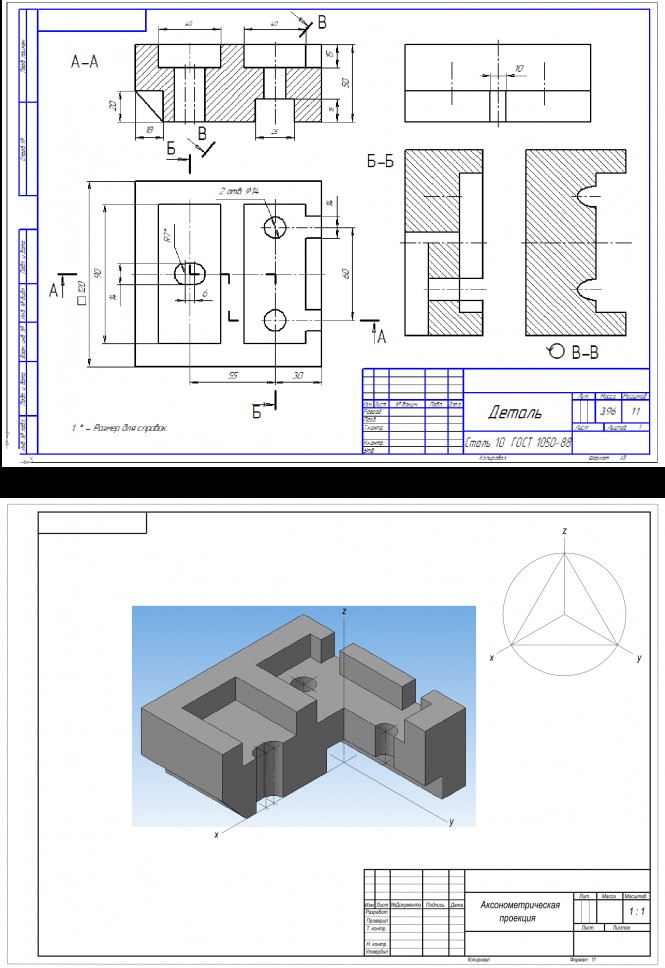
Построить третье изображение детали по двум данным, дать разрезы, построить натуральный вид наклонного сечения, а также наглядное изображение детали в аксонометрической проекции КомментарииОпределить угол между линией и плоскостью
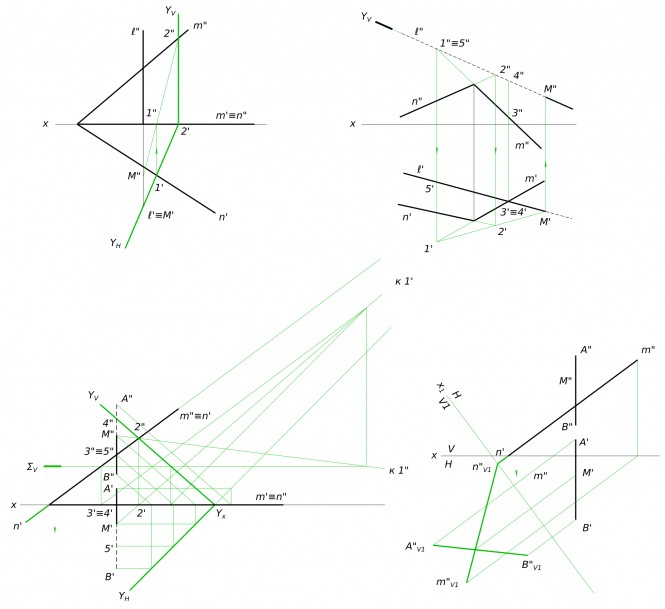
Определить угол между линией и плоскостью КомментарииПересечение линий и плоскостей
Пересечение линий и плоскостей КомментарииПересечение линий и плоскостей
Пересечение линий и плоскостей КомментарииВторая задача решена неверно.
Извините. Я допустил неточность в определении видимости прямой. А задача решена правильно.
А разве не нужно решать не с помощью третьей проекции?
Да, данные задачи принято решать без третьей проекции. Третья задача кроме того решена способом преобразования чертежа (плоскопараллельное перемещение).
На экзамене Вас могут попросить решить какую-либо из этих задач другим способом.
А не подскажите как второй пример решить с помощью третьей проекции?
Необходимо построить третью проекцию (профильную) и решать задачу в системе двух плоскостей проекций (V и W) в том же алгоритме.
Одна вспомогательная секущая плоскость через прямую
Спасибо большое!
Построить недостающую проекцию точки A, зная, что расстояние от точки а до прямой m, равно 30 мм.
Построить недостающую проекцию точки A, зная, что расстояние от точки A до прямой m, равно 30 мм и она расположена впереди нее. 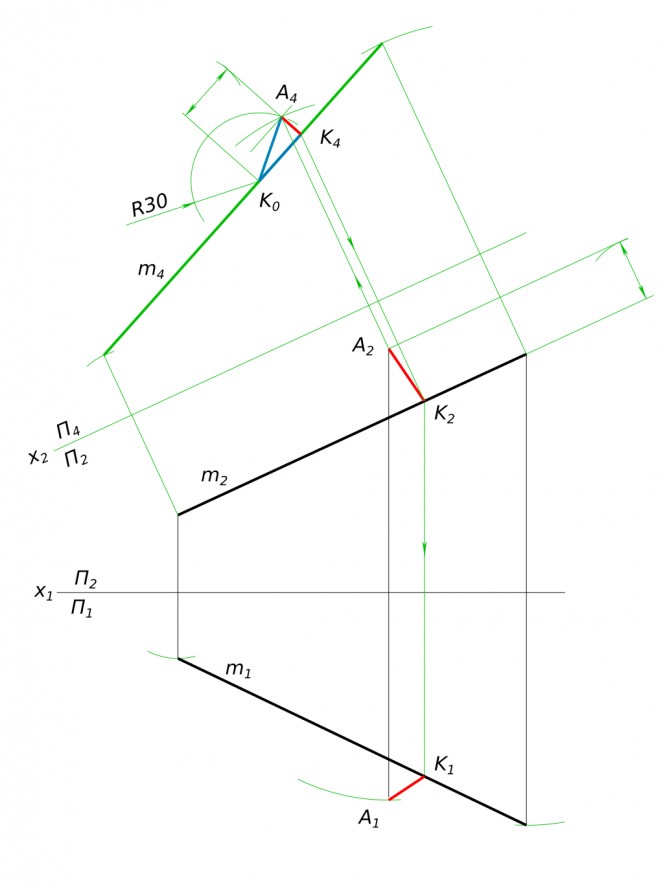
Построить недостающую проекцию точки A, зная, что расстояние от точки A до прямой m, равно 30 мм и она расположена впереди нее КомментарииПересечение линий и плоскостей
Пересечение линий и плоскостей КомментарииВ плоскости построить , горизонталь , фронталь и линию наибольшего ската.
В плоскости построить , горизонталь , фронталь и линию наибольшего ската. КомментарииПостроить точку пересечения прямой с плоскостью и определить видимость прямой относительно поскости
Построить точку пересечения прямой с плоскостью и определить видимость прямой относительно плоскости 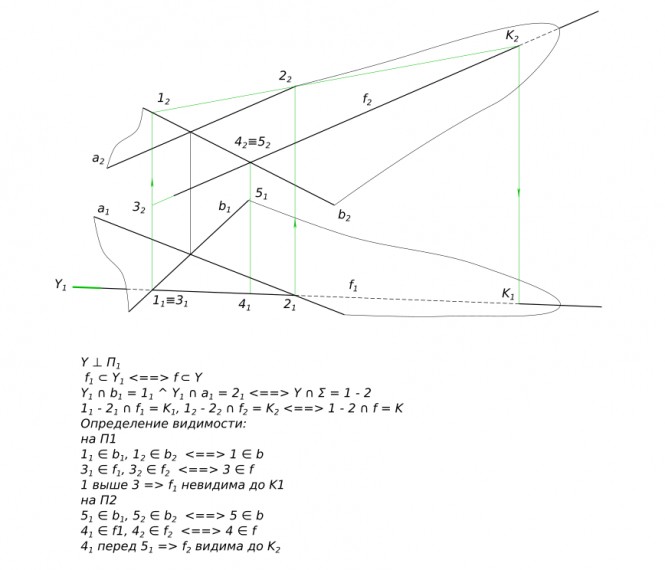
Построить точку пересечения прямой с плоскостью и определить видимость прямой относительно плоскости КомментарииСделать сопряжение сферы и цилиндра
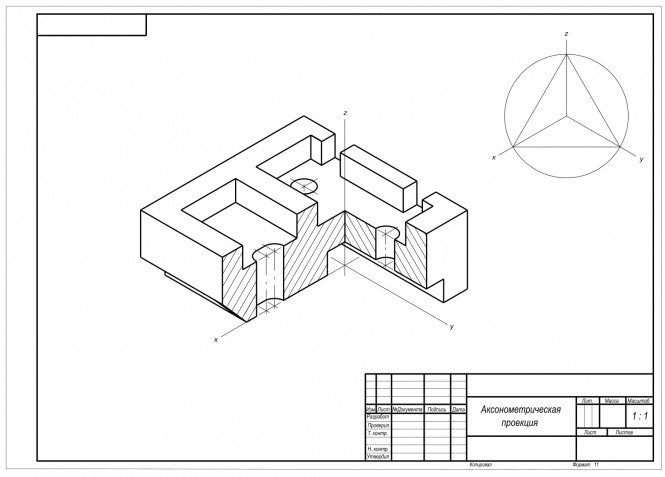
Сделать сопряжение сферы и цилиндра КомментарииПостроить проекции детали с сечением; выполнить прямоугольную изометрию с аксонометрическим вырезом
Построить проекции детали с сечением; выполнить прямоугольную изометрию с аксонометрическим вырезом |
Записать новую задачу Все задачи Все темы Все инженеры |



Комментарии