Все решения инженера @NICKПостроить вид слева. Выполнить фронтальный и профильный разрез(срединение половины вида с половиной разреза) .А-А не строить
Построить вид слева. Выполнить фронтальный и профильный разрез(соединение половины вида с половиной разреза) 
Построить вид слева. Выполнить фронтальный и профильный разрез(соединение половины вида с половиной разреза) По сборочному чертежу выполнить эскизы деталей 2, 3, 4 съёмника седла клапана головки блока автомобиля
По сборочному чертежу выполнить эскизы деталей 2, 3, 4 съёмника седла клапана головки блока автомобиля 
Выполнение по сборочному чертежу эскиза детали 3 съёмника седла клапана КомментарииДостроить горизонтальную проекцию плоскости треугольника ABC, если плоскость эта параллельна прямой EF.
Достроить горизонтальную проекцию плоскости треугольника ABC, если плоскость эта параллельна прямой EF.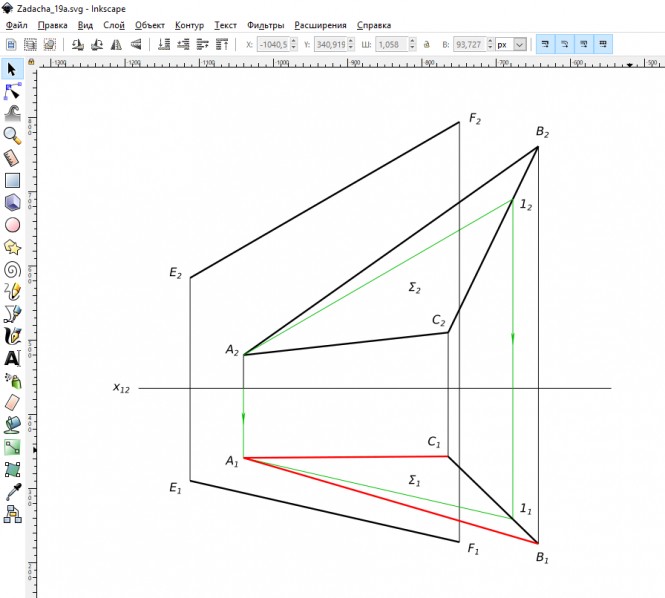 
Достроить горизонтальную проекцию плоскости треугольника ABC, если плоскость эта параллельна прямой EF. Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ EF ‖ Σ $
$ EF ‖ (A - 1) ⇔ E_{2}F_{2} ‖ (A_{2} - 1_{2}), E_{1}F_{1} ‖ (A_{1} - 1_{1}) $
$ Σ ⊃ A - 1 $
$ A ∈ Σ ∧ 1 ∈ Σ $ КомментарииПостроить горизонтальную проекцию прямой b . Найти на ней точку равноудаленную от плоскостей п2 и п1.
Построить горизонтальную проекцию прямой b . Найти на ней точку равноудаленную от плоскостей п2 и п1.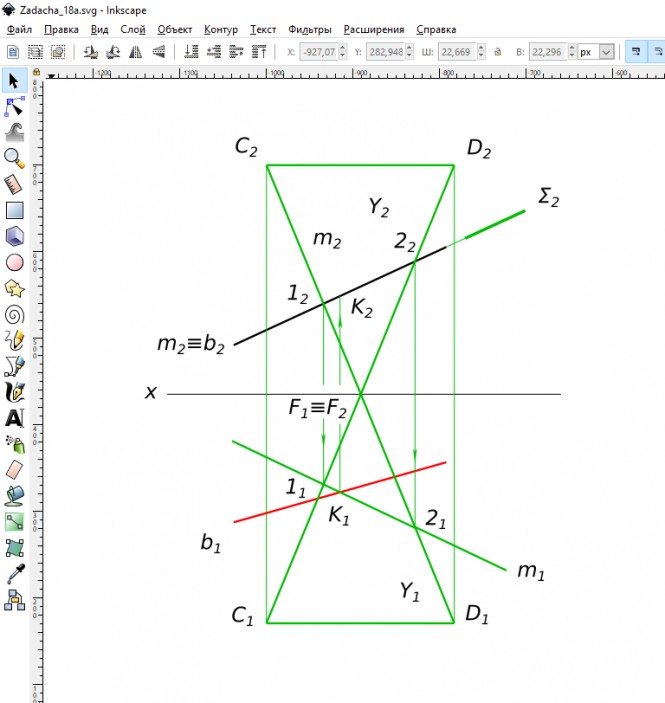 
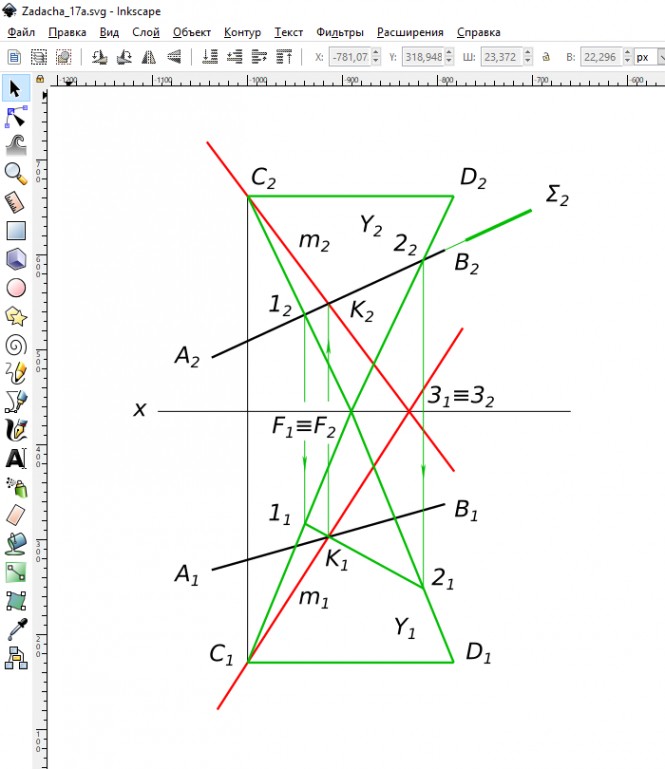
Построить горизонтальную проекцию прямой b . Найти на ней точку равноудаленную от плоскостей п2 и п1. КомментарииЧерез точку C провести прямую m пересекающую прямую AB и ось х
Через точку C провести прямую m пересекающую прямую AB и ось х Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ C ∈ m ⇔ C_{1} ∈ m_{1}, C_{2} ∈ m_{2} $
$ m ∩ x $
$ Y ⊃ m $
$ Σ ⊃ AB $
$ (1 - 2) = Σ ∩ Y $
$ K = (1 - 2) ∩ AB $
$ m ⊃ CK $
$ 3 = m ∩ x $ 
Через точку C провести прямую m пересекающую прямую AB и ось х КомментарииПостроить проекции точки A равноудаленной от трех плоскостей проекций, если A_{x}=70.
Построить проекции точки A равноудаленной от трех плоскостей проекций, если A_{x}=70.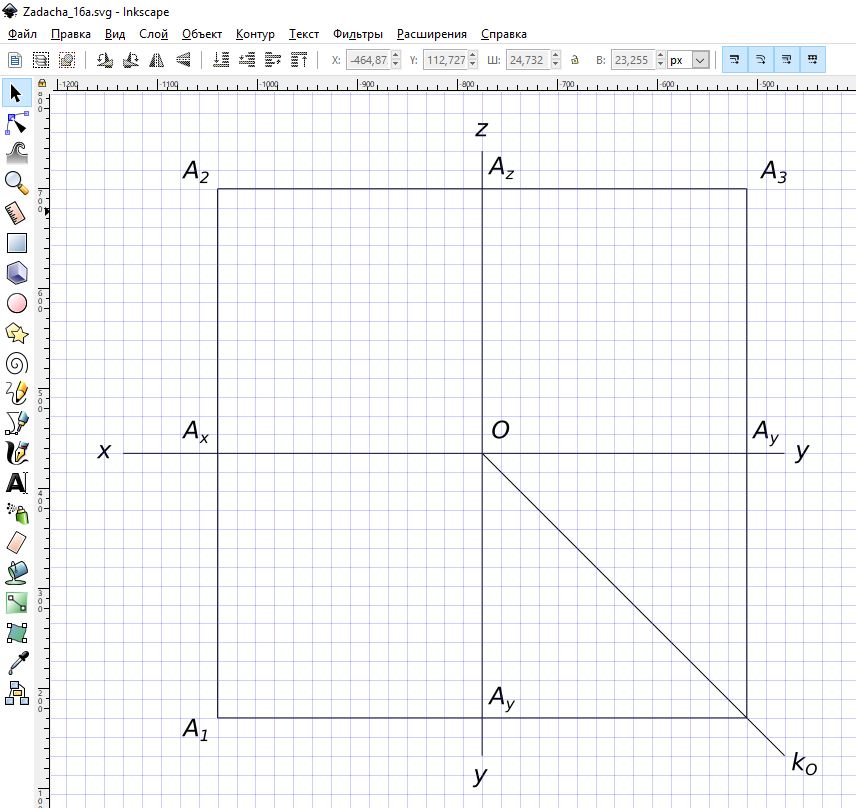 
Построить проекции точки A равноудаленной от трех плоскостей проекций, если A_{x}=70. Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ A_{x} = A_{y} = A_{z} = 70 $ КомментарииПостроить множество точек плоскости удаленных на заданную величину r
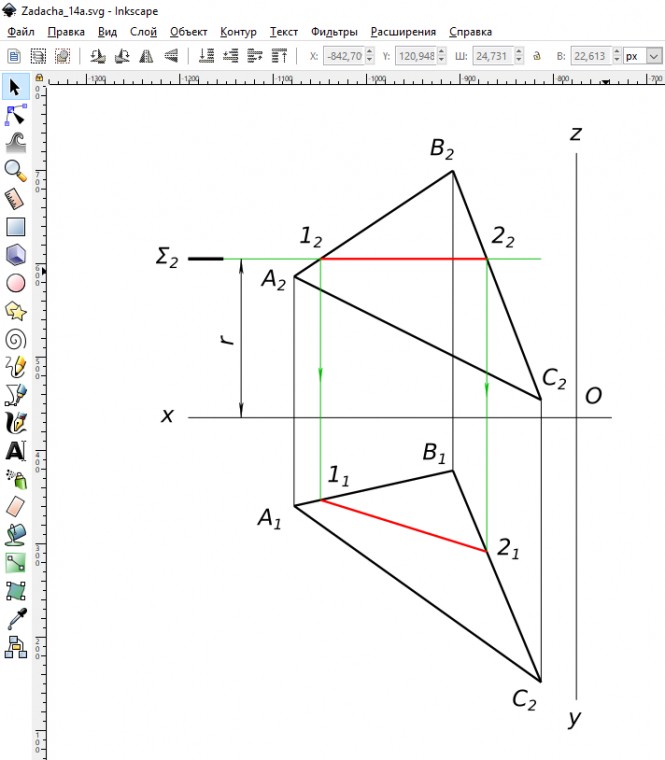
Построить множество точек плоскости треугольника ABC удаленных на заданную величину r от горизонтальной плоскости проекций. 
Построить множество точек плоскости удаленных на заданную величину r
$ 1 - 2 = Σ ∩ (ABC) $ КомментарииПостроить недостающие проекции точек A и B зная, что A лежит на плоскости П1 а точка B лежит на плоскости П2
Построить недостающие проекции точек A и B зная, что A лежит на плоскости П1 а точка B лежит на плоскости П2.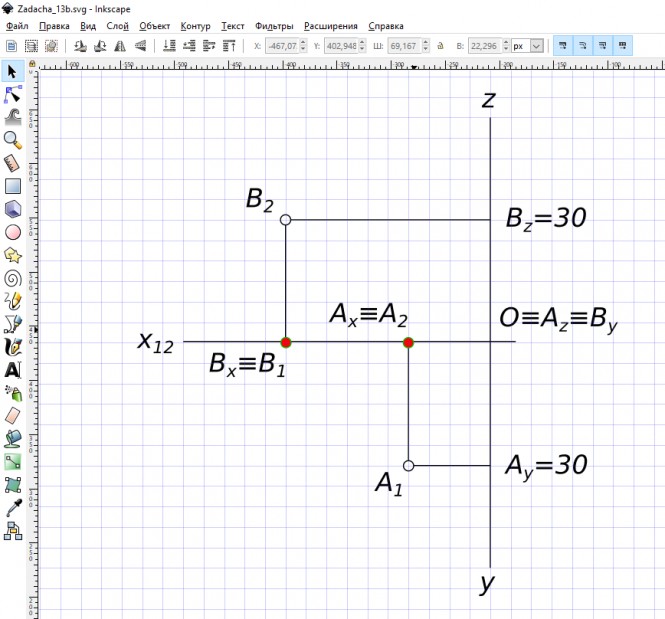 
Построить недостающие проекции точек A и B зная, что A лежит на плоскости П1 а точка B лежит на плоскости П2
$ A ∈ H ⇔ A_{2} ∈ x $
$ B ∈ V ⇔ B_{1} ∈ x $ КомментарииПостроить проекции точки B симметричной точке A относительно плоскости П1
Построить проекции точки B симметричной точке A относительно плоскости π1. Чтобы выполнить построение необходимо знать условие симметричности точек относительно π1.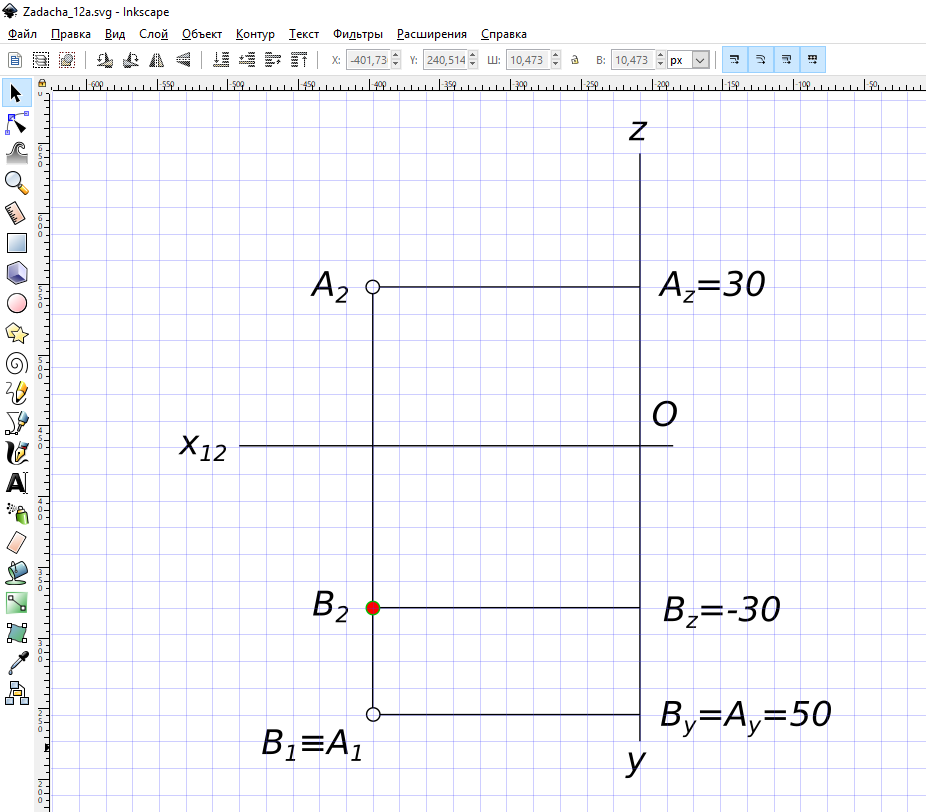 
Построить проекции точки B симметричной точке A относительно плоскости П1 По условию задачи точка B симметрична точке A, относительно плоскости π1 откуда следует вывод, что они находятся на перпендикуляре к π1 по разные стороны от нее на равном удалении. Ax=Bx; Ay=By и Bz=-Az Смотрите также: симметричность точки A относительно плоскостей П1, П2, П3 соответственно - https://ingr.fxyz.ru/tasks/2006/; симметричность точки A относительно осей ox, oy, oz соответственно - https://ingr.fxyz.ru/tasks/2007/. КомментарииЧерез точку А провести перпендикуляр к плоскости, заданной плоской фигурой и найти точку пересечения перпендикуляра с плоскостью
Через точку А провести перпендикуляр к плоскости, заданной плоской фигурой и найти точку пересечения перпендикуляра с плоскостью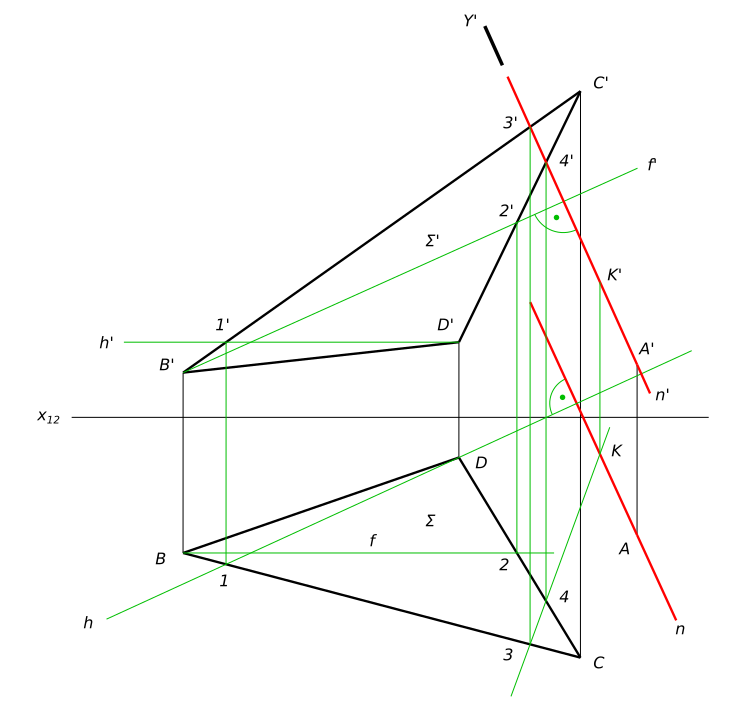 
Через точку А провести перпендикуляр к плоскости, заданной плоской фигурой и найти точку пересечения перпендикуляра с плоскостью Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ A ∈ n ⊥ Σ $
$ Σ ∩ Y ⊥ П_{2} = (3-4) $
$ n ∩ (3-4) = K $ КомментарииНа прямой ℓ найти точку, равноудаленную от точек A и B
На прямой ℓ(ℓ_{1}, ℓ_{2}) найти точку, равноудаленную от точек A(A_{1}, A_{2}) и B(B_{1}, B_{2})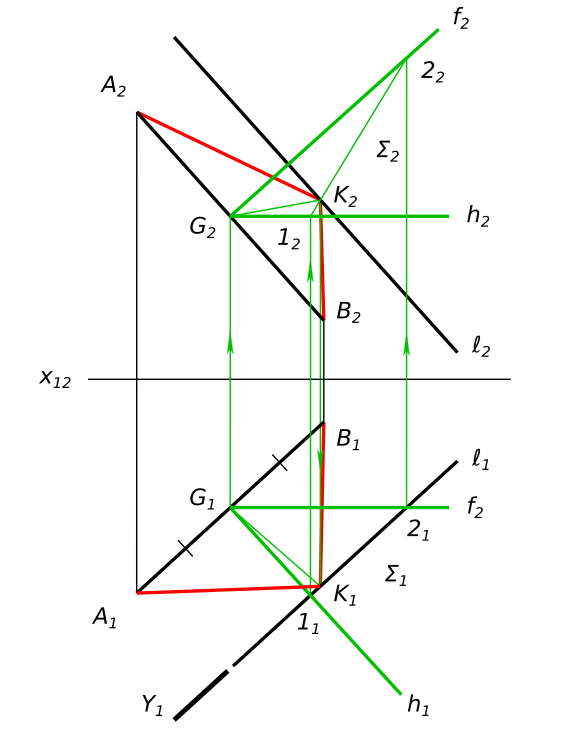 
На прямой ℓ найти точку, равноудаленную от точек A и B Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ \frac{AB}{2} = AG = BG ⇔ \frac{A_{1}B_{1}}{2} = A_{1}G_{1} = B_{1}G_{1} $
$ Σ(h ∩ f = G) ⊃ G ⇔ Σ_{1}(h_{1} ∩ f_{1} = G_{1}), Σ_{2}(h_{2} ∩ f_{2} = G_{2}) $
$ Σ ∩ Y ⊥ П_{1} = (1-2) $
$ ℓ ∩ (1-2) = K ⇔ ℓ_{1} ∩ (1_{1}-2_{1})=K_{1}, ℓ_{2} ∩ (1_{2}-2_{2})=K_{2} $
$ |AK| = |BK| $ КомментарииПостроить проекции точек B и C, равноудаленных от плоскостей проекций П_{1} и П_{2}
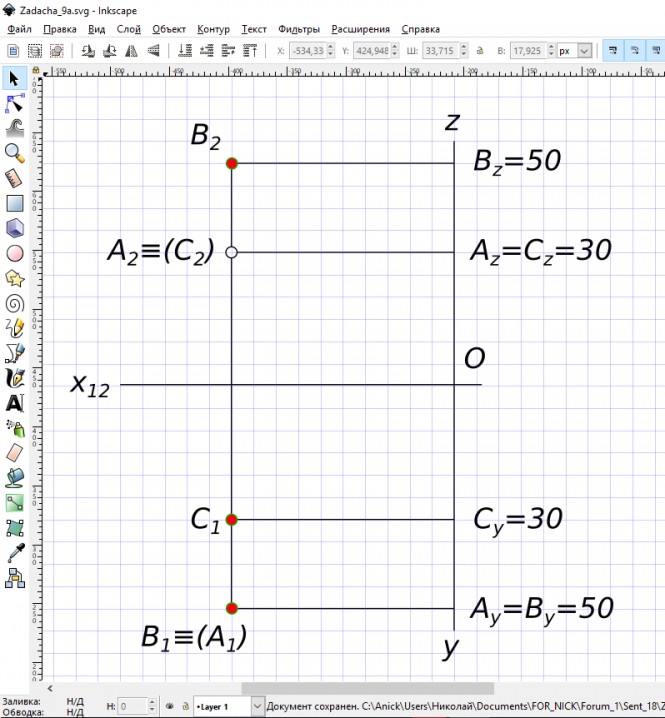
Построить проекции точек B и C, равноудаленных от плоскостей проекций П_{1} и П_{2} и конкурирующих с заданной точкой A : (B ↕ A)П_{1} и (C ↕ A)П_{2} 
Построить проекции точек B и C Точки B и C равноудалены от плоскостей проекций П_{1} и П_{2}, поэтому записываем
$ B_{y} = B_{z} = 50 $
$ C_{y} = C_{z} = 30 $ Точки A и B конкурируют относительно плоскости проекций П_{1}
$ (B ↕ A)П_{1} $ Точки A и C конкурируют относительно плоскости проекций П_{2}
$ (A ↕ C)П_{2} $ КомментарииПостроить прямую
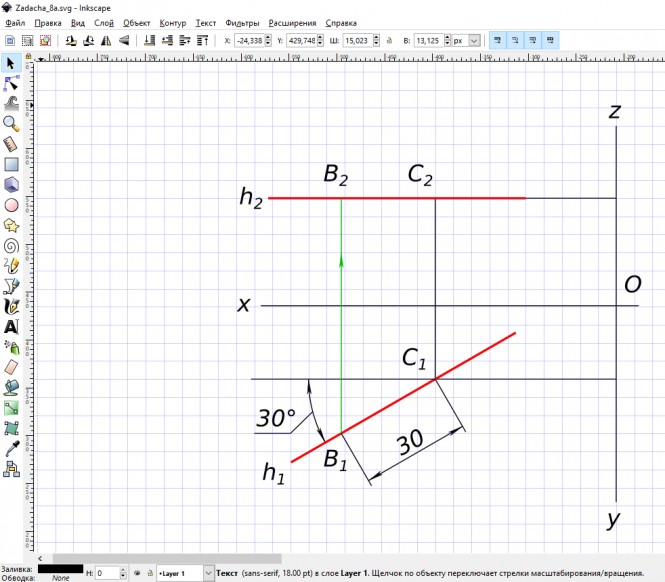
Через точку С (50; 20; 30) провести прямую, параллельную плоскости проекций П1, и расположенную под углом 30 градусов к плоскости проекций П2. На прямой найти точку В, удаленную от точки С на 30 мм 
Через точку С (50; 20; 30) провести прямую
$ C ∈ h ⇔ C_{1} ∈ h_{1}, C_{2} ∈ h_{2} $
$ h ‖ П_{1} ⇔ h_{2} ‖ Ox ⇒ C_{1}B_{1} = |CB| = 30 мм $
$ B ∈ h ⇔ B_{1} ∈ h_{1}, B_{2} ∈ h_{2} $ КомментарииПостроить проекции сферы
Дан отрезок AB(A1-B1, A2-B2). Построить проекции сферы с центром в точке A. Радиус сферы равен длине отрезка AB. Или. Дан отрезок AB(A1-B1, A2-B2). Построить проекции сферы. Точка A - ее центр. Точка B принадлежит поверхности сферы.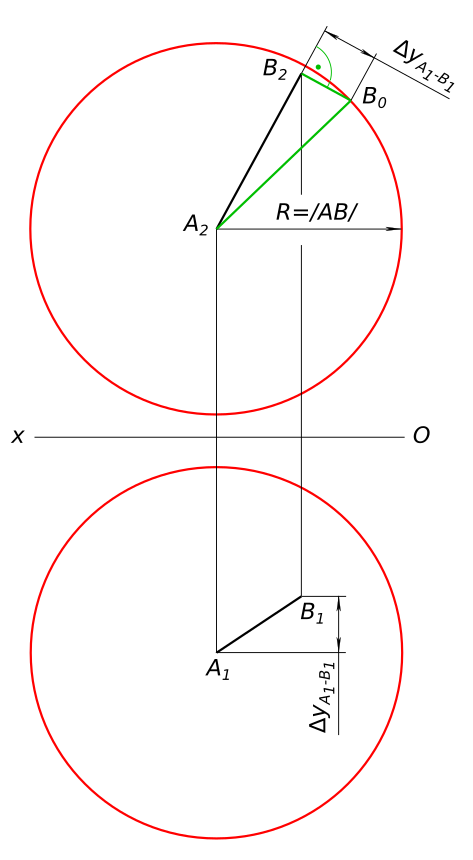 
Построение проекций сферы КомментарииОпределить недостающую проекцию точки
Определить недостающую проекцию точки A(A1, ?), если известно, что точка удалена от прямой f на 25 мм.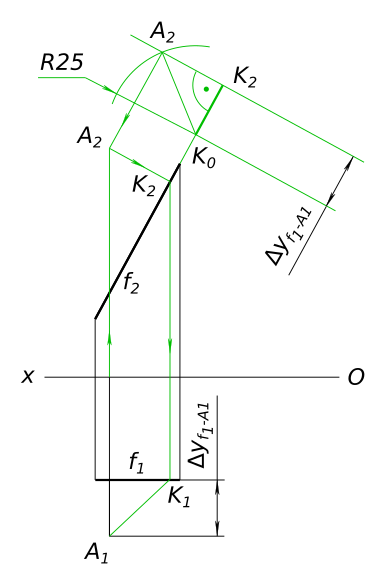 
Определить недостающую проекцию точки Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ A ∉ f(f_{1}, f_{2}) $
$ f ‖ П_{2} ⇔ f_{1} ‖ Ox $ Используя частное положение прямой f составим уравнение расстояния до точки A
$ K ∈ f, AK ⊥ f ⇔ A_{2}K_{2} ⊥ f_{2} $
$ /AK/ = A_{2}K_{0}} = 25 мм, $
$ AK ⇔ A_{1}K_{1}, A_{2}K_{2} ⇒ A_{2} $ КомментарииПостроить третье изображение детали по двум данным, дать разрезы, построить натуральный вид, наклонного сечения.
Построить третье изображение детали по двум данным, дать разрезы, построить натуральный вид, наклонного сечения, а также наглядное изображение детали в аксонометрической проекции.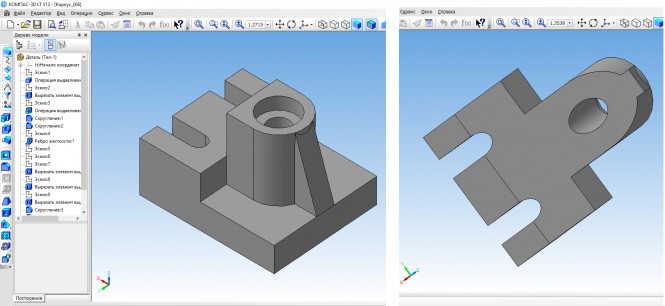 
Построить третье изображение детали по двум данным, дать разрезы, построить натуральный вид, наклонного сечения, а также наглядное изображение детали в аксонометрической проекции КомментарииПостроить множество точек удаленных на заданную величину r от прямой m
Построить множество точек удаленных на заданную величину r от прямой m. Если r=25.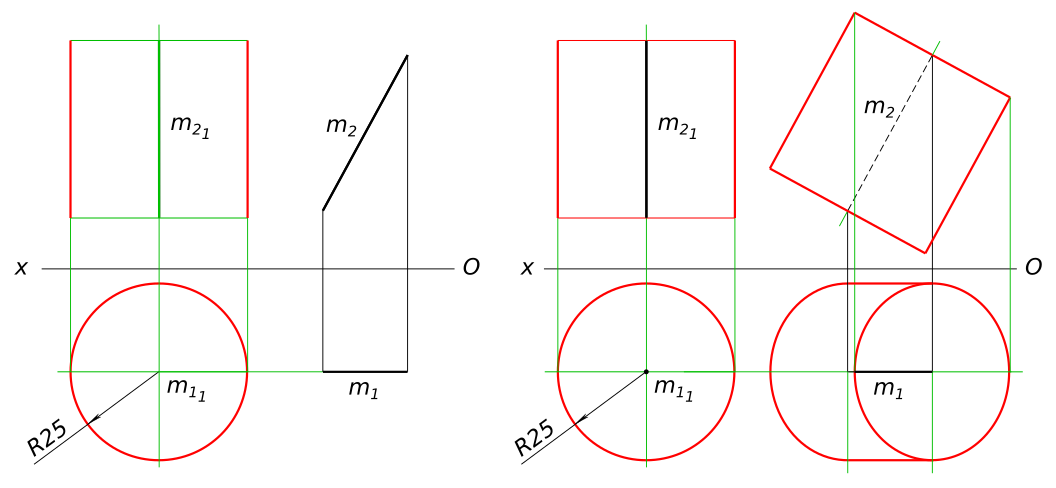 
Построение множества точек удаленных на заданную величину r от прямой m Комментарии2) Через точку А(35,?,50) провести отрезок фронтальной прямой AD=50, пересек. EK под прямым углом. E(70,40,35), K(15,10,5).
Через точку А(35,?,50) провести отрезок фронтальной прямой AD=50, пересекающий EK под прямым углом. Если E(70,40,35), K(15,10,5). 
Через точку А(35,?,50) провести отрезок фронтальной прямой Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ AD ⊥ EK ∧ AD ∩ EK $
$ G = AD ∩ EK ⇔ A_{1}D_{1} ∩ E_{1}K_{1}, A_{2}D_{2} ∩ E_{2}K_{2} $ КомментарииЧерез точку А провести фронтально-проецирующую плоскость, параллельную отрезку МК А(25;25;20) М(55;30;25) К (25;15;10)
Через точку А провести фронтально-проецирующую плоскость, параллельную отрезку МК. Если А(25;25;20), М(55;30;25) и К(25;15;10).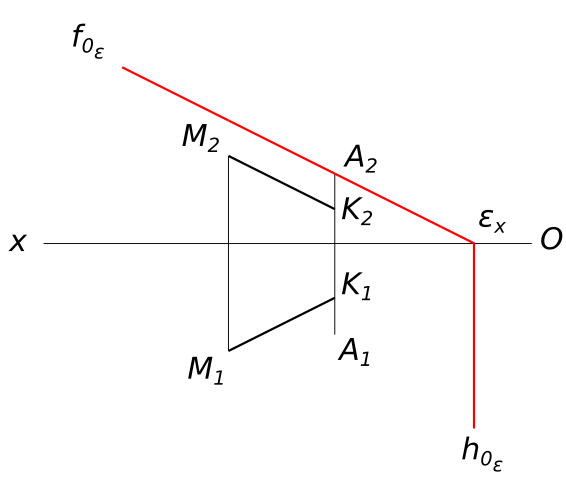 
Через точку А провести фронтально-проецирующую плоскость Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ A ≡ f_{0_{ε}} ∧ f_{0_{ε}} ‖ M_{2}K_{2} $
$ h_{0_{ε}} ⊥ Ox $
$ f_{0_{ε}} ‖ M_{2}K_{2} ⇔ ε ‖ MK $ КомментарииЗаключить точку B(B1, B2) в плоскость ε. Задать эту плоскость следами h_{1_{ε} и h_{2_{ε}}. Задана точка схода следов ε_{x}.
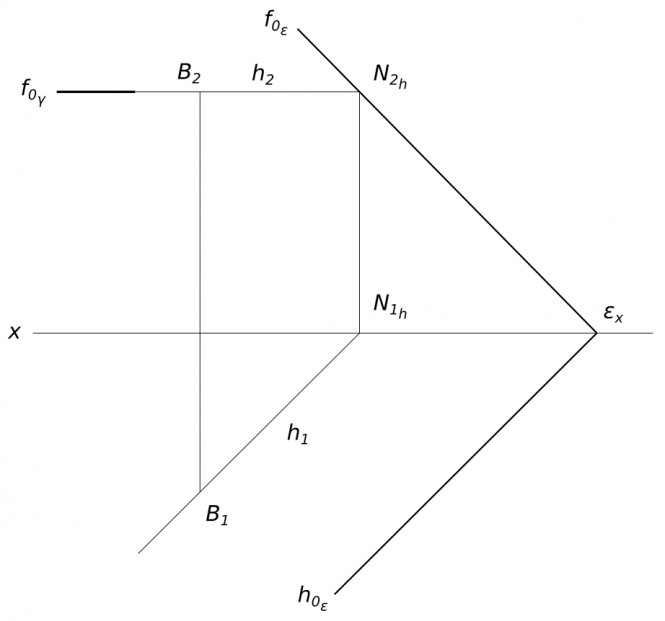
Заключить точку B(B1, B2) в плоскость ε, задав эту плоскость следами h_{1_{ε} и h_{2_{ε}}. Задана точка схода следов ε_{x}. 
Заключение точки B(B1, B2) в плоскость h_{0_{ε} и f_{0_{ε}} Через заданную точку B проводим вспомогательную фронтально проецирующую плоскость γ горизонтального уровня (параллельную плоскости П_{1}). Вспомогательная плоскость γ пересекает заданную по прямой h. Заданная точка B лежит на линии пересечения плоскостей. Используюя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:
$ B ∈ γ ⇔ B_{2}∈ f_0_{γ} $
$ γ ∩ ε = h $
$ B ∈ h ∧ h ∈ ε ⇒ B ∈ ε $ КомментарииПостроить три проекции куба со срезами под углом 45
КомментарииПостроить три проекции куба со срезами под углом 45
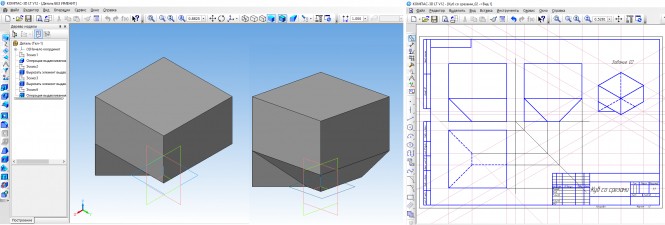
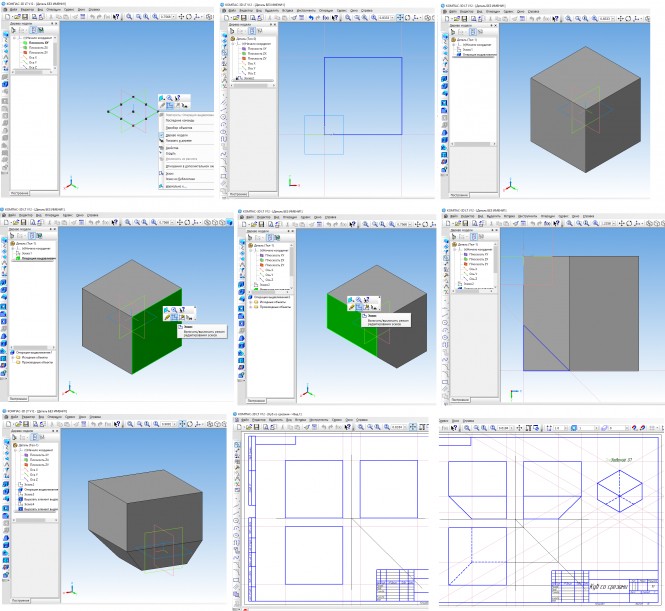
Построить три проекции куба со срезами под углом 45 
Построение трех проекций куба со срезами под углом 45 КомментарииПостроить три проекции куба со срезами под углом 45
Построить три проекции куба со срезами под углом 45 
Построение трех проекций куба со срезами под углом 45 Куб ограничен шестью гранями - верхняя и нижняя грани это его основания, а остальные грани называют боковыми. В пересечении боковых граней находятся ребра именуемые также боковыми. Остальные ребра куба относят к его основаниям верхнему или нижнему. Анализируя рисунок задания отмечаем, что только одно боковое ребро сохранило свой размер - дальнее от зрителя ребро. Остальные три боковых ребра стали короче. Также укоротились ребра нижнего основания. Выполнение задания можно начать с создания 3D модели куба со срезами, осваивая на простом примере работу с программой КОМПАС. Далее создаем чертеж сначала полного куба, а затем и усеченного. КомментарииСоздать 3d модель зубчатого колеса
Если принять высоту головки зуба h' = m и высоту ножки h" = 1,2m, то расчетным путем находим остальные параметры зубчатого колеса: диаметр окружности выступов
$ D_{e} = mz + 2m = m(z+2) $ Откуда находим модуль зацепления
$ m = \frac{D_{e}}{z+2} = \frac{56}{12+2} = 4 мм $ диаметр начальной окружности
$ d = mz = 4 × 12 = 48 мм $ диаметр окружности впадин
$ D_{i} = d - 2h" = d - 2,4m = 48 - 9,6 = 38,6 мм $ диаметр основной окружности
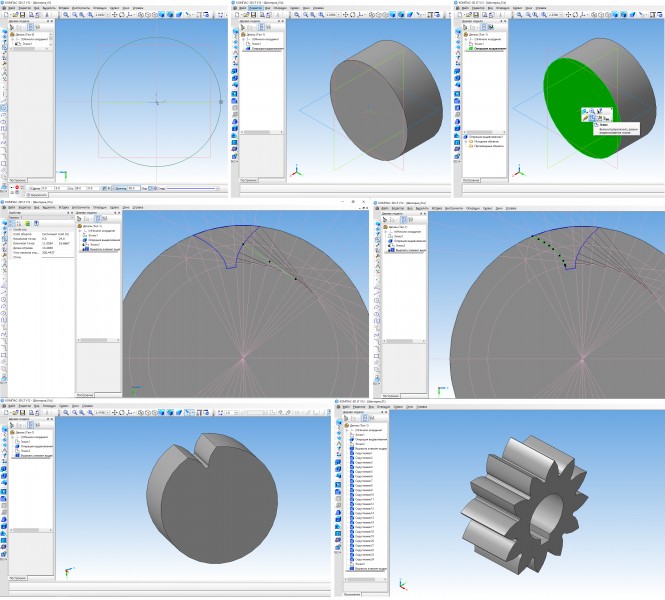
$ D_{o} = dcos(20°)} = 48 × 0,94 = 45,12 мм $ Создаем 3d модель зубчатого колеса: 
Создание 3d модели зубчатого колеса создаем эскиз вырезаемого элемента, расположенного между двумя смежными зубьями. Вычерчиваем эвольвенту: из точки пересечения начальной окружности с вертикальной осью проводим касательную прямую к основной окружности. Измеряем отрезок на касательной определяя тем самым длину развернутой части окружности.
$ L_{дуги} = φ_{рад}R_{осн} $ Откуда находим угол
$ φ_{рад] = \frac{L_{дуги}}{R_{осн}} $ Который делим на четыре равные части и рассчитав по формуле длины дуг откладываем их в виде отрезков на соответствующих им касательных получаем точки для построения эвольвенты от основной до начальной окружности. Точки эвольвенты от начальной окружности до окружности выступов строим аналогично. Рассчитываем длину дуги шага зацепления
$ t = πm $ Ей соответствует угол
$ φ = \frac{360}{12}= 30° $ Разделив этот угол пополам получаем линию симметрии зуба и строим его вторую половину. Достраиваем вырезаемый элемент и делаем операцию вырезать выдавливанием. Затем, выполнив копирование элемента по окружности, делаем вырезание остальных зубьев. КомментарииПостроить третий вид по двум данным, выполнить рациональные разрезы
Построить третий вид по двум данным, выполнить рациональные разрезы 
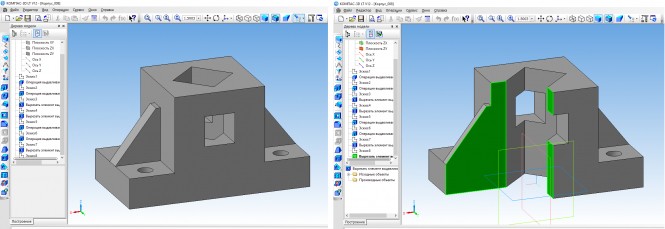
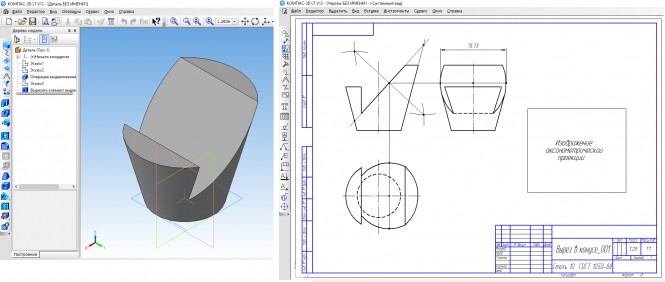
Построить третий вид по двум данным, выполнить рациональные разрезы КомментарииПостроить две проекции конуса вращения со сквозным вырезом по одной имеющейся. Построить развертку его боковой поверхности
Построить две проекции конуса вращения со сквозным поперечным вырезом по одной имеющейся. Построить развертку его боковой поверхности Поверхность выреза - цилиндр, потому вписываем в него правильную 16 - гранную призму и находим точки встречи ее ребер с поверхностью конуса способом вспомогательных секущих плоскостей.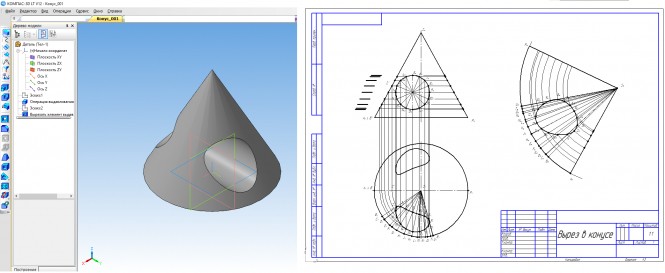 
Построить две проекции конуса вращения со сквозным вырезом по одной имеющейся. Построить развертку его боковой поверхности Данные для построения развертки
Угол в радианах
$ φ_{рад}= \frac{φ_{град}×π}{180} $ Длина дуги по окружности основания
$ L = φ_{рад}×R = φ_{рад}×55 $ Угол развертки в градусах
$ φ_{град} = \frac{φ_{рад}×180}{π} $ КомментарииПо двум данным построить три изображения детали,выполнить рациональное разрезы,нанести размеры.Построить прямоугольную изометрию
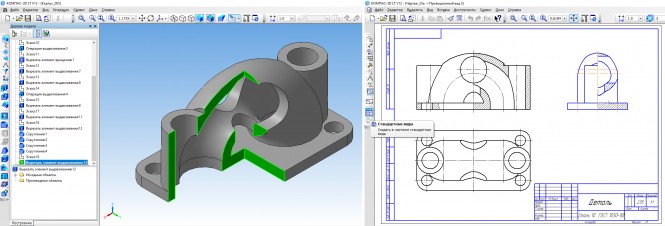
По двум данным построить три изображения детали,выполнить рациональное разрезы,нанести размеры.Построить прямоугольную изометрию детали с вырезом ее 1/4 части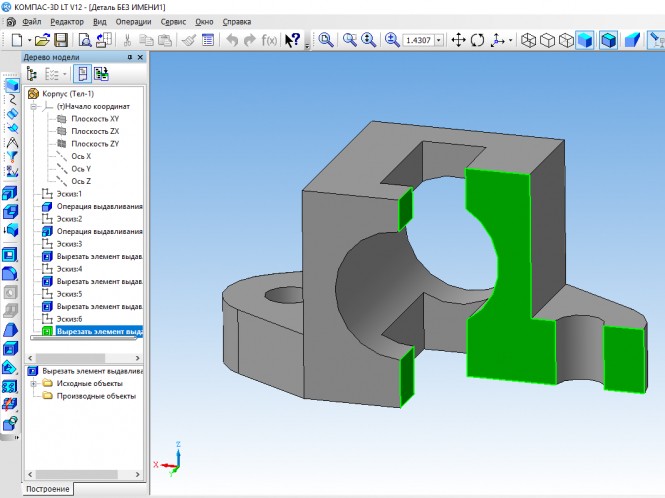 
По двум данным построить три изображения детали,выполнить рациональное разрезы,нанести размеры.Построить прямоугольную изометрию детали с вырезом ее 1/4 части КомментарииПо натурной модели разработать чертеж пробкового крана в двух изображениях
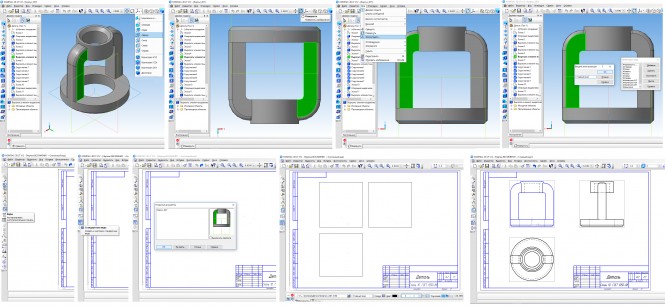
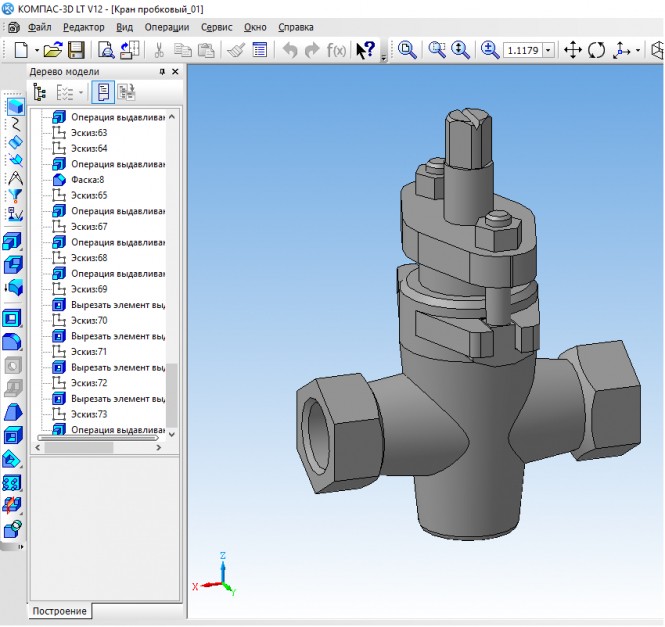
По натурной модели разработать чертеж пробкового крана в двух изображениях 
Натурная модель пробкового крана, разработанная по сборочному чертежу КомментарииПостроить три изображения криволинейной поверхности с вырезом.
Построить три изображения криволинейной поверхности с вырезом 
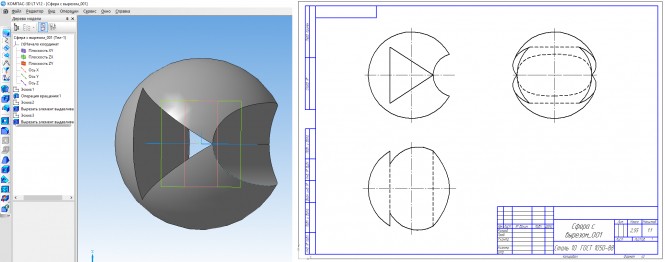
Построить три изображения криволинейной поверхности с вырезом КомментарииПостроить горизонтальную проекцию и аксонометрию данной геометрической фигуры(вариант 10)
Построить горизонтальную проекцию и аксонометрию данной геометрической фигуры 
Построить горизонтальную проекцию и аксонометрию данной геометрической фигуры Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии