На прямой ℓ найти точку, равноудаленную от точек A и B

На прямой ℓ(ℓ_{1}, ℓ_{2}) найти точку, равноудаленную от точек A(A_{1}, A_{2}) и B(B_{1}, B_{2})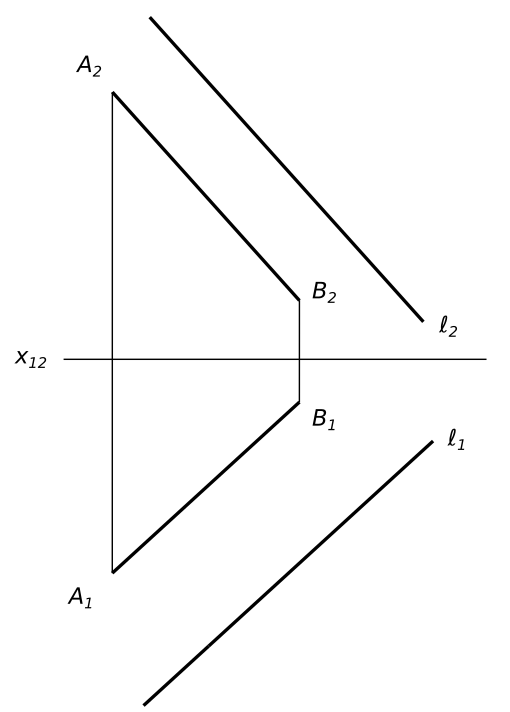

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

поставьте оценку:

1 голосов, средний бал: 5.0000

На прямой ℓ(ℓ_{1}, ℓ_{2}) найти точку, равноудаленную от точек A(A_{1}, A_{2}) и B(B_{1}, B_{2})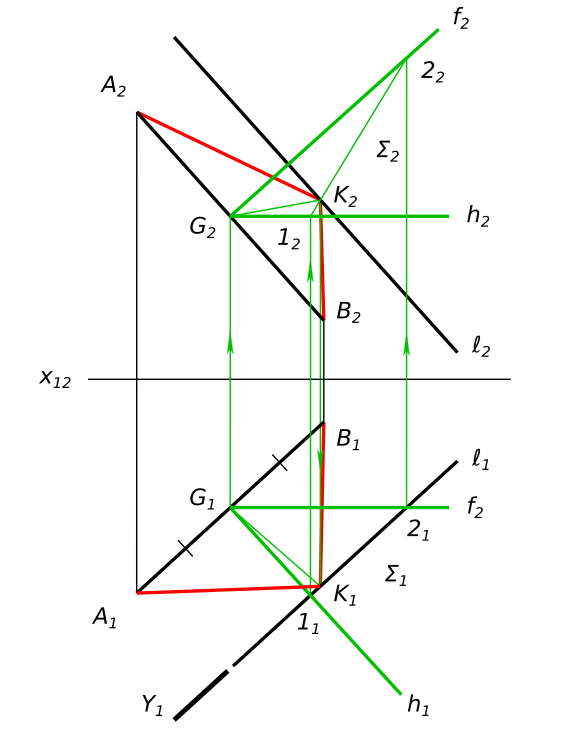

На прямой ℓ найти точку, равноудаленную от точек A и B

Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем:

$ \frac{AB}{2} = AG = BG ⇔ \frac{A_{1}B_{1}}{2} = A_{1}G_{1} = B_{1}G_{1} $

$ Σ(h ∩ f = G) ⊃ G ⇔ Σ_{1}(h_{1} ∩ f_{1} = G_{1}), Σ_{2}(h_{2} ∩ f_{2} = G_{2}) $

$ Σ ∩ Y ⊥ П_{1} = (1-2) $

$ ℓ ∩ (1-2) = K ⇔ ℓ_{1} ∩ (1_{1}-2_{1})=K_{1}, ℓ_{2} ∩ (1_{2}-2_{2})=K_{2} $

$ |AK| = |BK| $