|
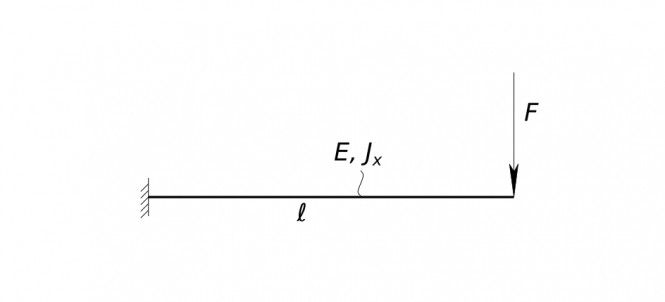
Балка нагруженная силой. Дана консольная балка нагруженная на конце силой F Требуется построить эпюру внутренних изгибающих моментов и эпюру внутренней перерезывающей силы. Решения задачиБалка нагруженная силой. Стержень работающий на изгиб называется балкой. Балка заделанная с одного конца называется консоль. Расчетная схема балки 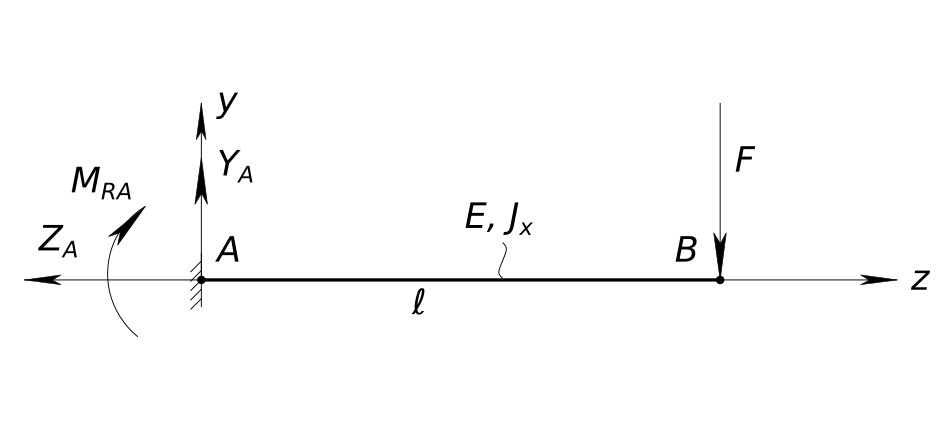
Балка нагруженная силой ℓ - длина балки Jx - момент инерции относительно главной центральной оси х E - модуль упругости материала балки EJx - изгибная жесткость Стержневая конструкция, все стержни которой лежат в одной плоскости и в этой же плоскости деформируются, называется плоской конструкцией. Для решения задачи вводим систему координат: оси z, x и y. Указываем на расчетной схеме реакции заделки соответствующие нагружению балки силой: горизонтальную, вертикальную и угловую. Реакции - это силы с которыми опоры действуют на стержень Z_{A} - горизонтальная реакция Y_{A} - вертикальная реакция M_{RA} - угловая реакция (моментная реакция) Находим реакции, составляя уравнения равновесия балки Первое уравнение - сумма всех сил в проекции на ось Y равна нулю
$ ΣF_{y}=Y_{A}-F=0 $ из него находим
$ Y_{A}=F $ Второе уравнение - сумма всех сил в проекции на ось Z равна нулю
$ ΣF_{z}=-Z_{A}=0 $ Из него находим Z_{A}=0
$ Z_{A}=0 $ Третье уравнение - сумма всех моментов относительно точки A равна нулю. Момент силы принято считать положительным, если он вращает балку против часовой стрелки и наоборот - если по часовой стрелке. Учитывая, что плечи реакций Y_{A} и Z_{A} равны нулю
$ ΣM_{A}=-M_{RA}-F ℓ=0 $ из него получаем
$ M_{RA}=-F ℓ $ КомментарииБалка нагруженная силой Рисуем силовую схему 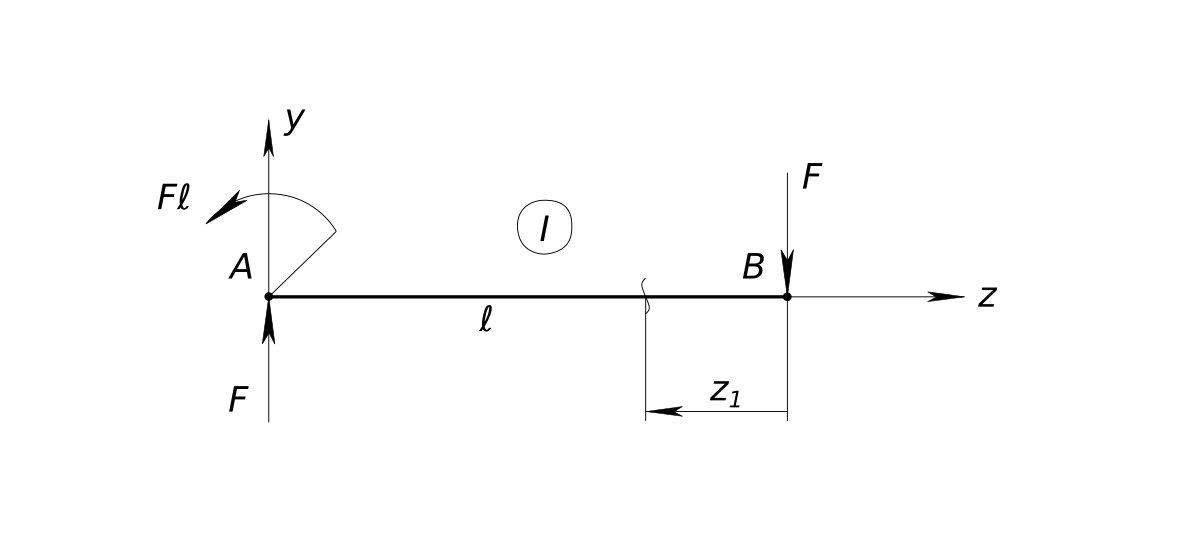
Балка нагруженная силой Четвертое (проверочное) уравнение - сумма всех моментов относительно точки B равна нулю.
$ ΣM_{B}=-F ℓ+F ℓ=0 $ Далее разбиваем стержень на участки. Границами участка служат концы балки. Нагрузка приложена к концу балки. Изменения геометрии сечения балки нет. Получаем один участок. Далее на каждом участке вводим локальные системы координат. Оси Z которых направлены вдоль оси балки к центру участка. КомментарииБалка нагруженная силой Следующим шагом используем метод определения внутренних силовых факторов. Мысленно разрезаем балку, отбрасываем левую часть. 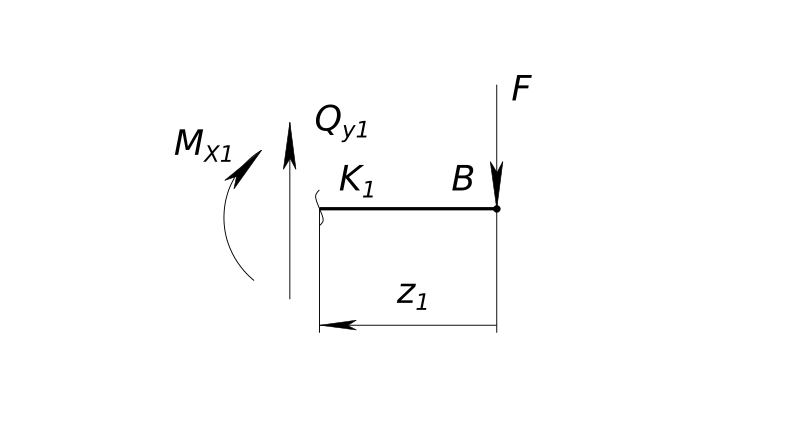
Балка нагруженная силой Заменяем действие отброшенной части силовыми факторами - Q_{y1}, M_{x1}. Пока не знаем их величину, но рисуем их в положительных направлениях, согласно установленному правилу знаков. Составляем уравнения равновесия Сумма всех сил в проекции на ось y_{1} равна нулю
$ ΣF_{y_{1}}=0=Q_{y_{1}}-F $ тогда
$ Q_{y_{1}}=F $ Сумма всех моментов относительно точки K_{1} равна нулю
$ ΣM_{K_{1}}=0=-M_{x_{1}}-Fz_{1} $ тогда
$ M_{x_{1}}=-Fz_{1} $ В точке B
$ z_{1}=0; M_{x_{1}}=-F×0=0 $ В точке A
$ z_{1}=ℓ; M_{x_{1}}=-F ℓ $ Реактивный момент M_{x_{1}} найден со знаком минус. А это означает, что действительное направление RA противоположно принятому при составлении уравнения равновесия. Исправляем направление RA на расчетной схеме. КомментарииБалка нагруженная силой По полученным расчетам строим эпюры внутренних силовых факторов - эпюр перерезывающей силы и эпюр моментов . 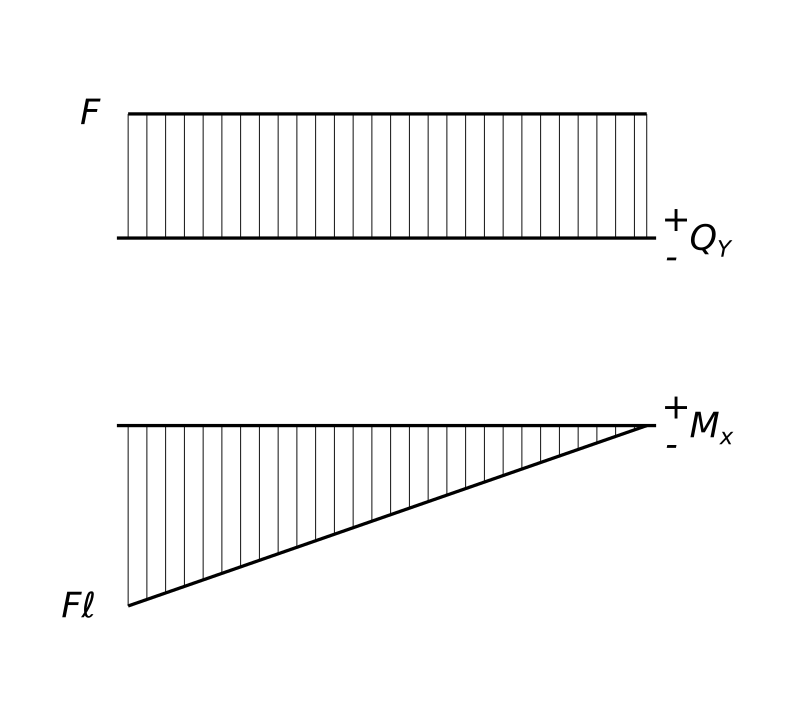
Балка нагруженная силой Эпюра перерезывающей силы Q_{y} выше с нулевой линии. В любом сечении перерезывающая сила равна F
$ Q_{y} = F $ Эпюра моментов M_{x} показывает, что момент действующий на участке не постоянный и отрицательный его величина линейно возрастает от конца балки к ее заделке, достигая наибольшего значения равного
$ M_{x} = F ℓ $ КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |

Комментарии