Все решения инженера @NICKОпределить длину отрезка АВ и построить фронтальный и горизонтальный следы прямой АВ.
Определить длину отрезка АВ и построить фронтальный и горизонтальный следы прямой АВ. 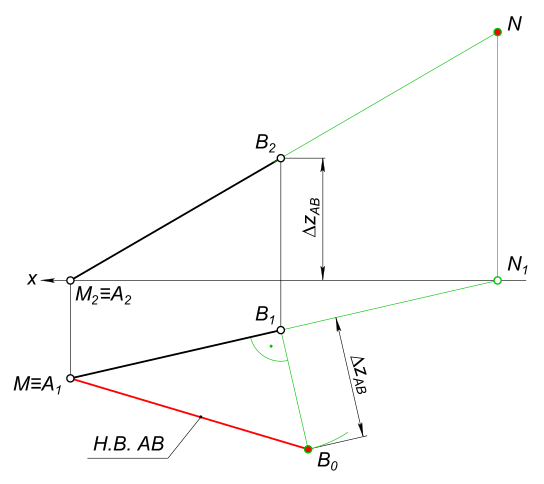
Определить длину отрезка АВ и построить фронтальный и горизонтальный следы прямой АВ В плоскости α заданной проекциями фигуры ∆ABC: 1. Определить положение принадлежащей ей точки D (недостающую проекцию); 2. Постр
В плоскости α заданной проекциями фигуры ∆ABC: 1. Определить положение принадлежащей ей точки D (недостающую проекцию); 2. Построить фронталь f(f', f") и горизонталь h(h', h") через точку A(A', A"); 3. Найти проекции следов фронтали M(M', M") и горизонтали N(N', N"); 4. Обозначить на чертеже углы наклона фронтали и горизонтали к плоскостям проекций. Комментариисделать эскиз резца (2 вида)
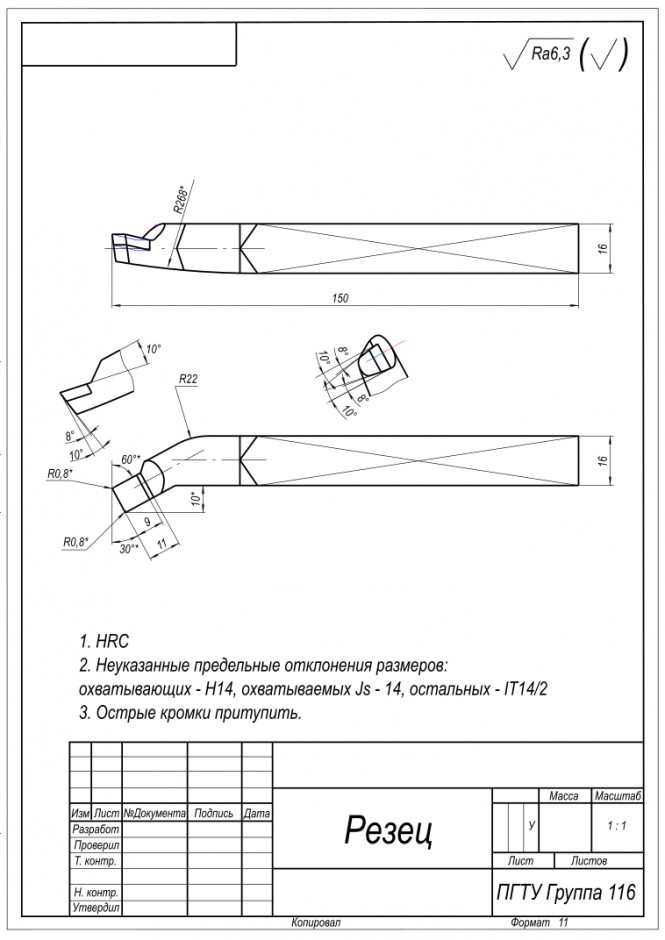
Выполнить эскиз резца по натурному образцу КомментарииПостроить три изображения многогранника с вырезом.
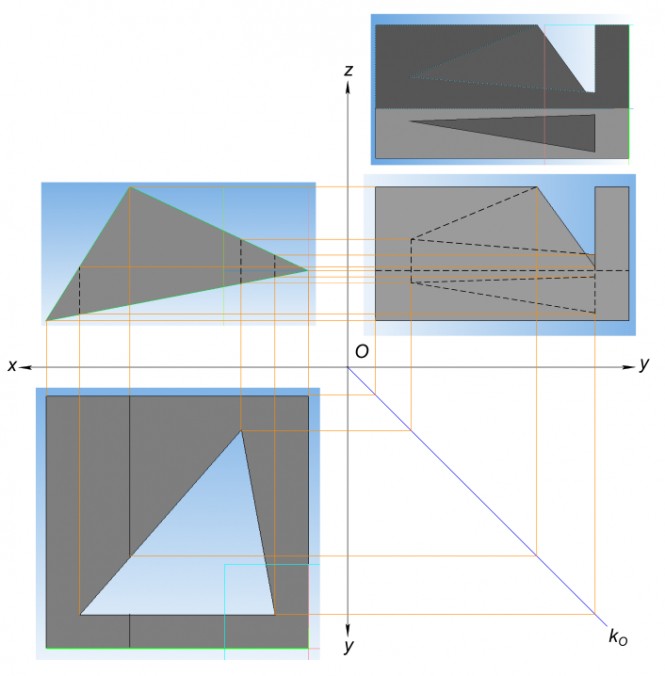
Построить три изображения многогранника с вырезом КомментарииПостроить три изображения многогранника и сечения многогранника плоскостью. Определить натуральную величину сечения.
Построить три изображения многогранника и сечения многогранника плоскостью. Определить натуральную величину сечения. 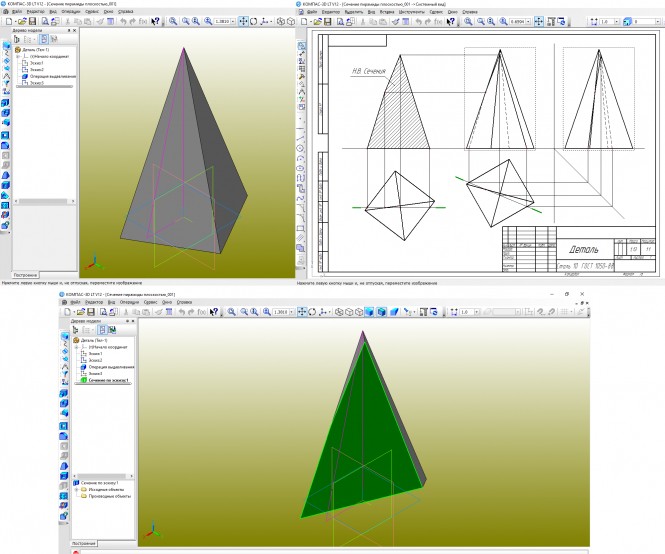
Построить три изображения многогранника и сечения многогранника плоскостью. Определить натуральную величину сечения КомментарииПостроить три изображения поверхности вращения и сечения поверхности плоскостью. Определить натуральную величину сечения.
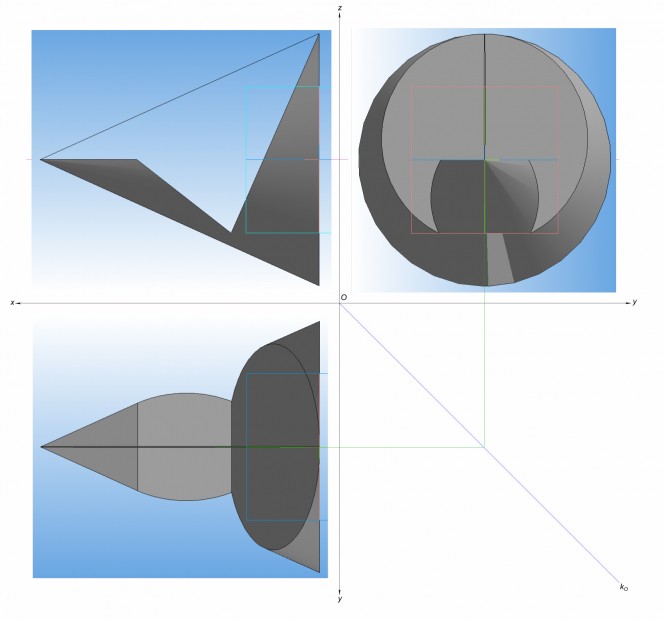
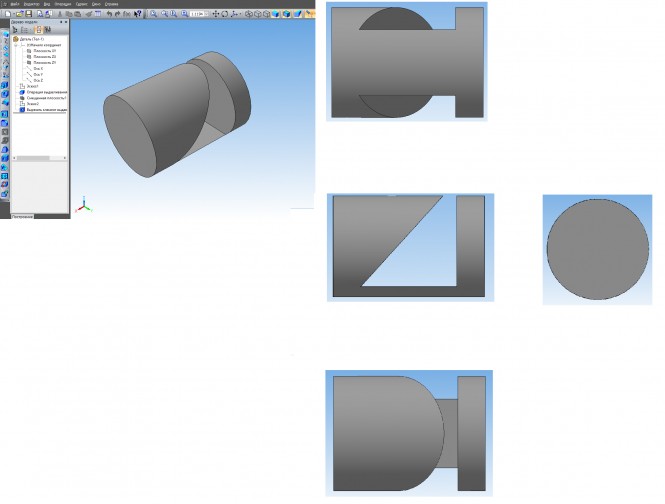
Построить три изображения поверхности вращения и сечения поверхности плоскостью. Определить натуральную величину сечения. КомментарииПостроить три изображения поверхности вращения с вырезом.
Построить три изображения поверхности вращения с вырезом КомментарииОпределить натуральную величину одного из треугольников (ABC или DEK) способом замены плоскостей проекций (табл. 1).
Определить натуральную величину треугольника ABC способом замены плоскостей проекций Данные задачи:
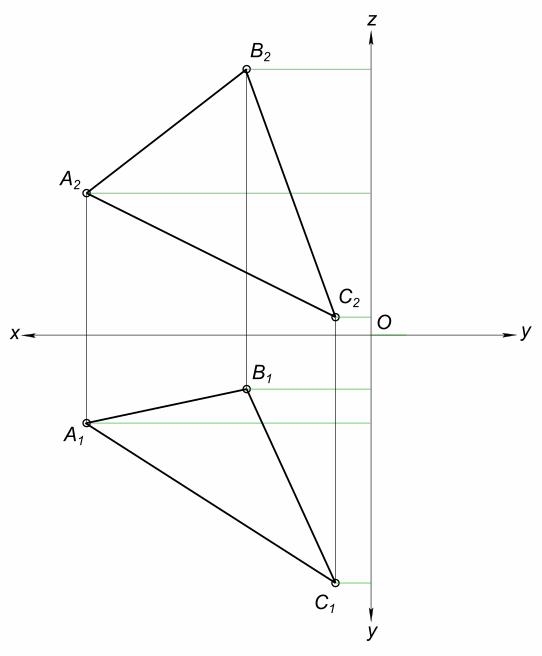
Способ перемены плоскостей проекций Я начал решать Вашу задачу. Продолжите ее решение каким либо способом. Например в на листе бумаги или в графическом редакторе. Продолжение решения размещайте на странице этой задачи. Если возникнут при этом вопросы, задавайте их в комментарии. КомментарииЗдравствуйте. Хотел Вас поблагодарить за то, что Вы помогаете. Для меня данные задачи пока еще сложные, мы не изучали инженерную графику. Для достижения необходимых знаний потребуется некоторое время. Я всего лишь студент 1 курса. Хотел у Вас спросить, те задачи которые вы уже решили, как правильно их нужно оформлять?
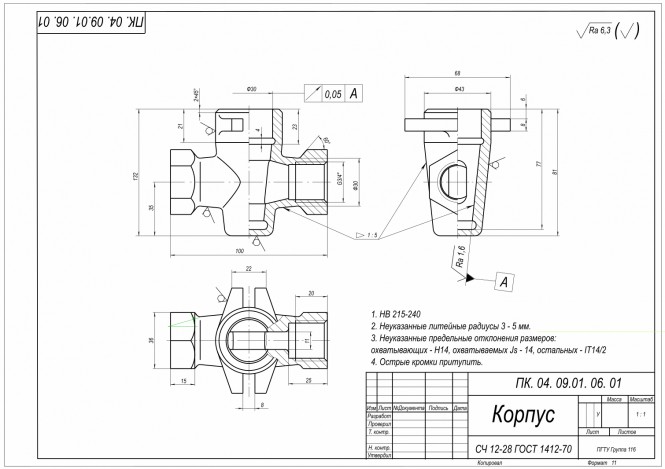
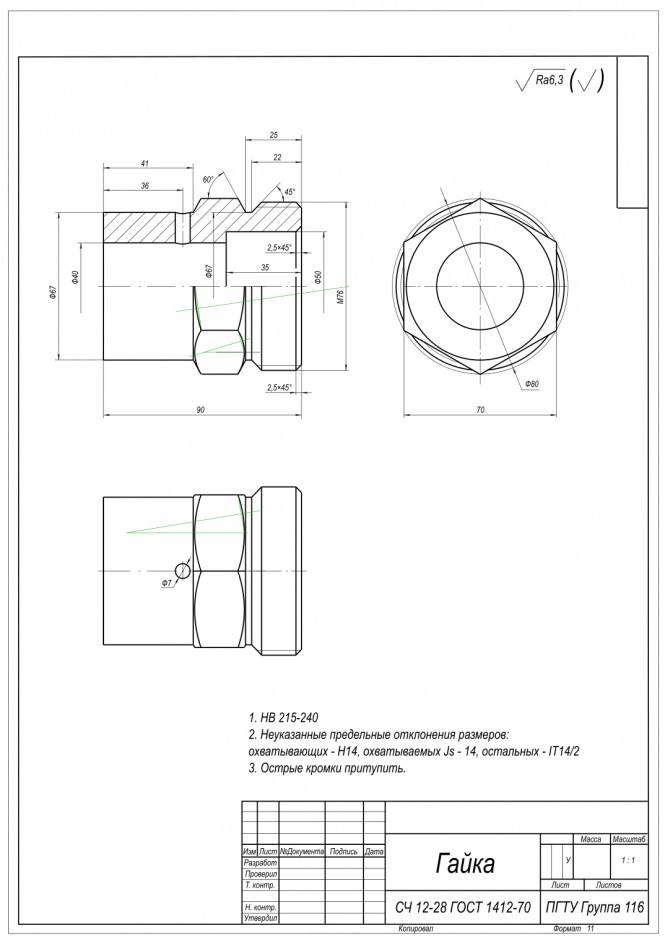
Необходимо выполнить чертежи деталей по их натурным моделям
Выполнить чертежи деталей по их натурным моделям КомментарииБлагодарю ! Вы меня очень выручили !
Построить три вида: фронтальный и профильный разрезы детали.
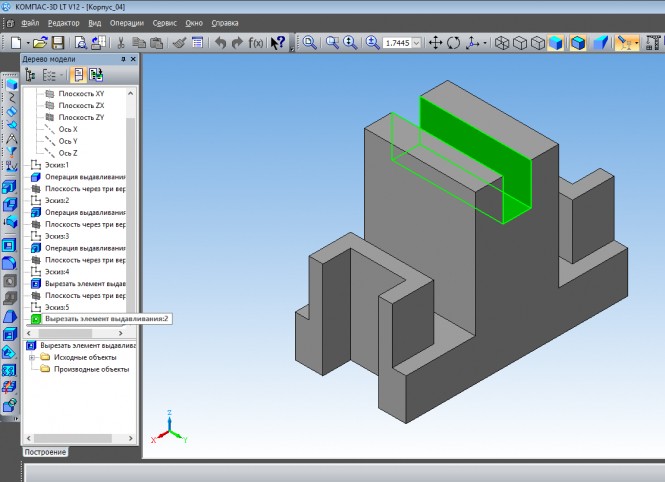
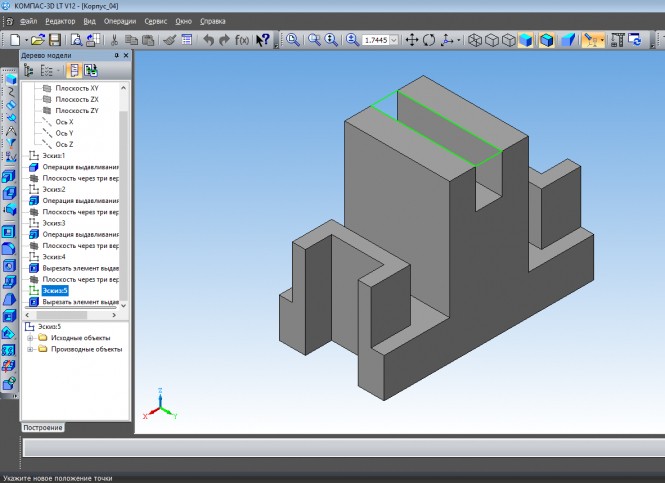
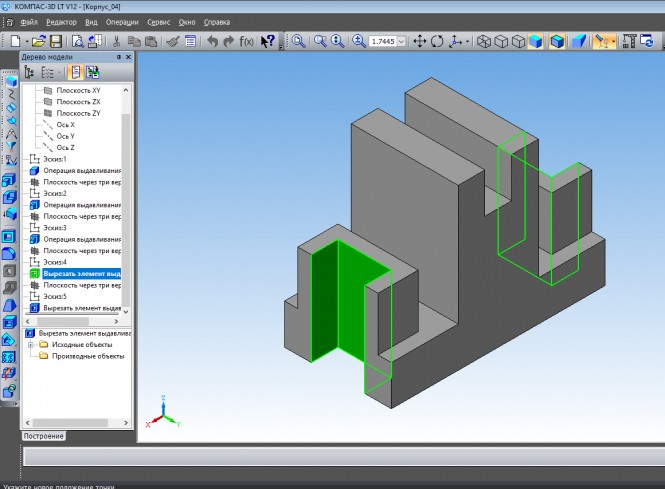
Построить три вида: фронтальный и профильный разрезы детали.Начертить прямоугольную изометрическую проекцию детали с вырезом 1/4 её части 
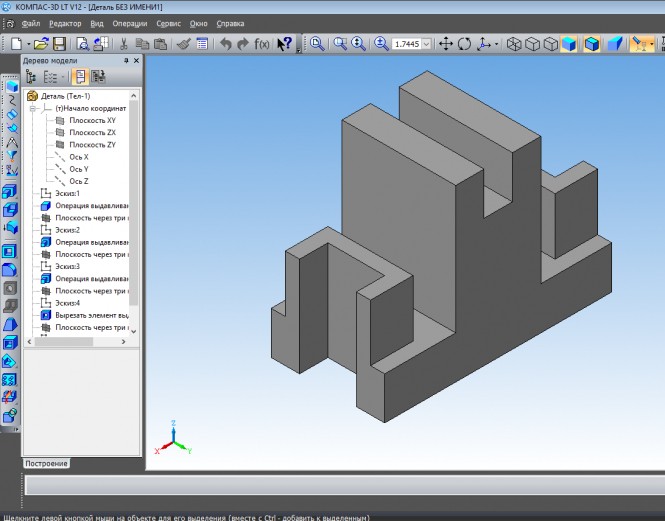
Деталь с вырезом 1/4 её части. Дерево модели. КомментарииПостроить три вида: фронтальный и профильный разрезы детали.
Построить три вида: фронтальный и профильный разрезы детали. Начертить прямоугольную изометрическую проекцию детали с вырезом 1/4 её части 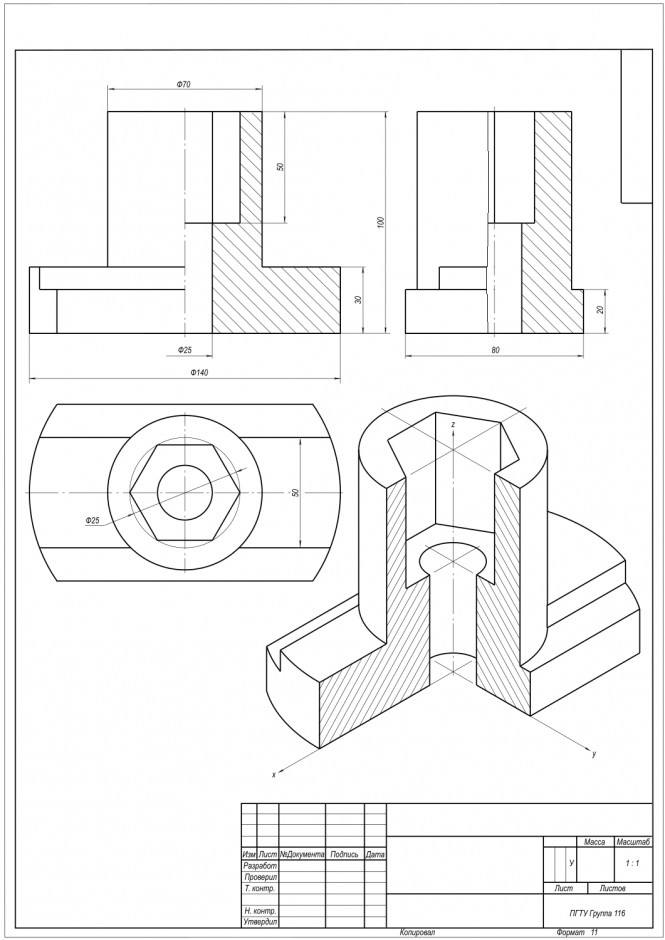
Построить три вида: фронтальный и профильный разрезы детали. Начертить прямоугольную изометрическую проекцию детали с вырезом 1/4 её части КомментарииНеобходимо выполнить схему , каждый элемент самой детали начертить .
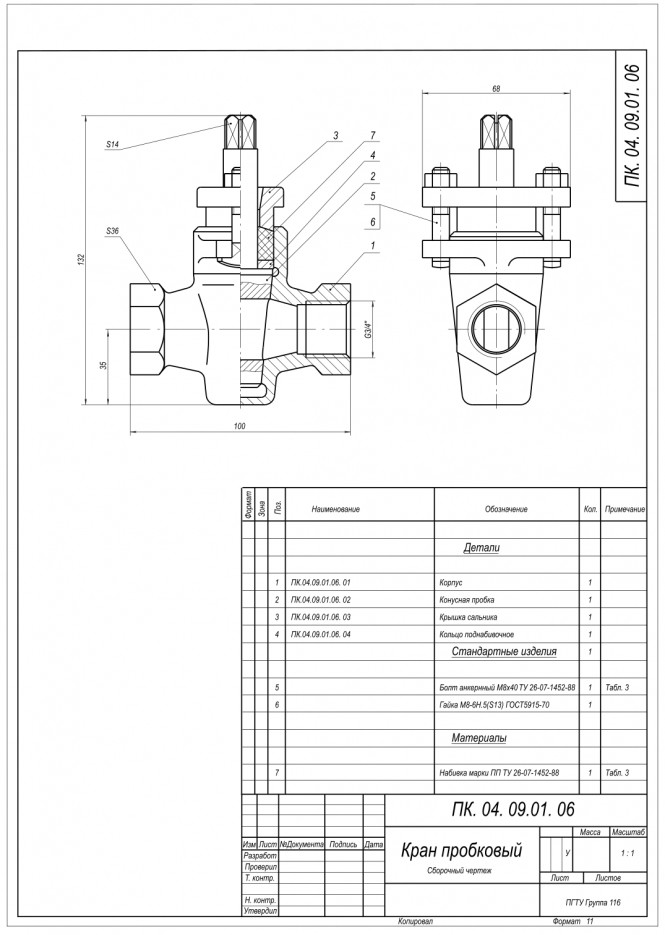
Выполнить схему пробкового крана 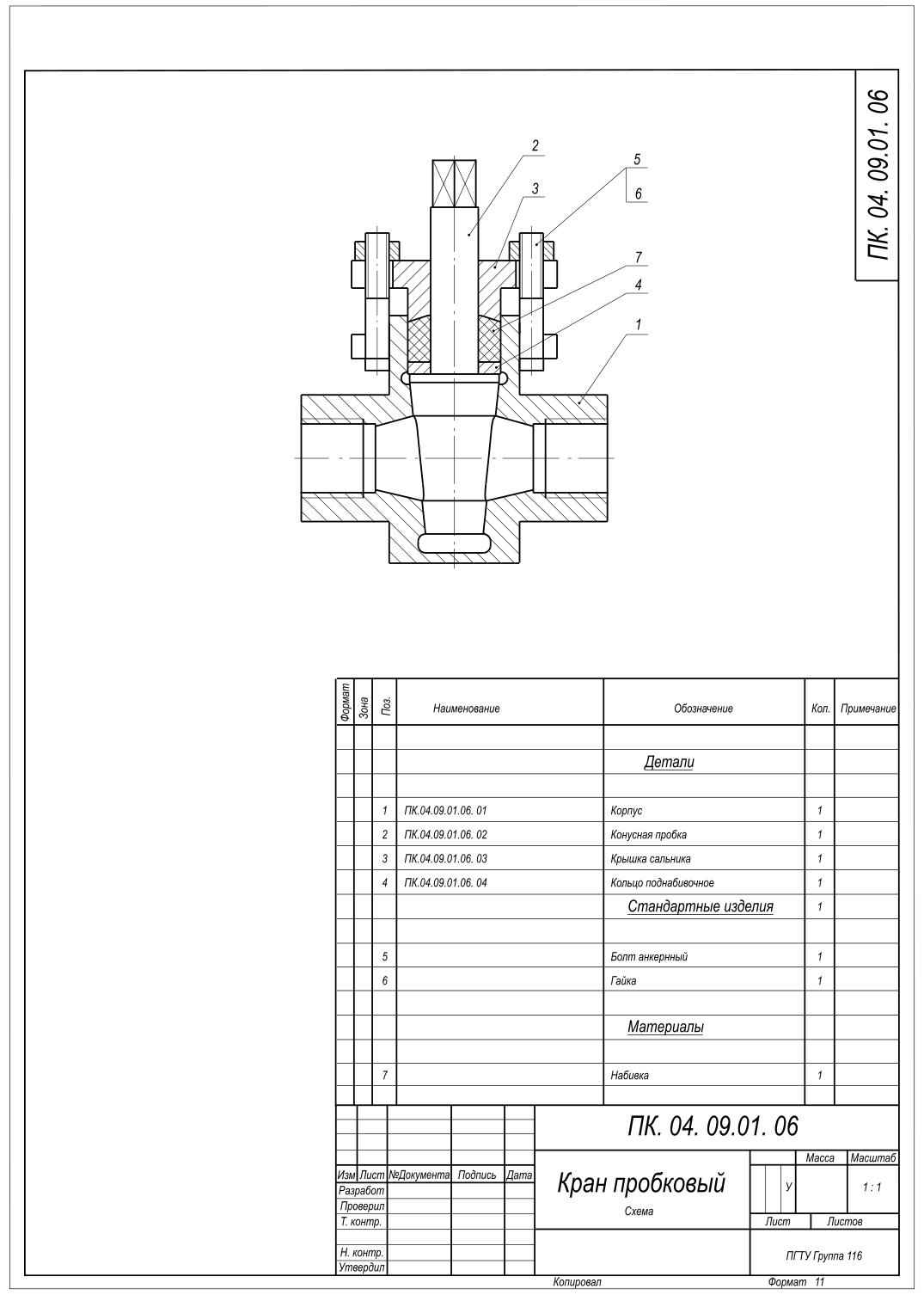
Схема пробкового крана К схеме изделия или его сборочному чертежу принято давать описание работы оного. По натурной модели разработать чертеж пробкового крана в двух изображениях
По натурной модели разработать чертеж пробкового крана в двух изображениях Построить равнобедренный треугольник
Построить равнобедренный треугольник ABC, если заданы его высота - отрезок CM и известно, что вершина A принадлежит П1, вершина B - П2 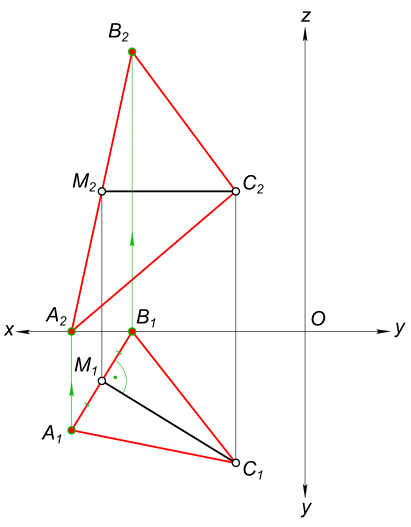
Построение равнобедренного треугольника Анализ исходного чертежа:
$ C_{2}M_{2} ‖ xO ⇒ CM - горизонталь $ По условию задачи
$ CM ⊥ AB $ Тогда
$ \vect{A_{1}B_{1}} ⊥ C_{1}M_{1} $ Откуда находим, учитывая условие задачи
$ B_{1} = \vect{A_{1}B_{1}} ∩ xO $ и
$ M_{1}A_{1} = M_{1}B_{1} $ Находим
$ A_{2} = линия связи ∩ xO $ Находим
$ \vect{A_{2}B_{2}} ≡ A_{2}M_{2} $ Находим
$ B_{2} = \vect{A_{2}B_{2}} ∩ линия связи $ КомментарииПостроить прямую m, пересекающую заданные прямые под прямым углом
Построить прямую m, пересекающую заданные прямые b(b1, b2) и d(d1, d2) под прямым углом 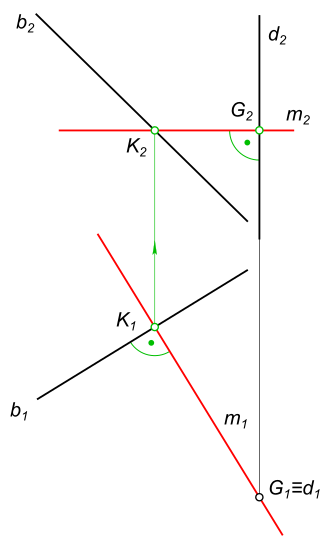
Прямая пересекает заданные прямые под прямым углом Анализ исходного чертежа:
$ b(b1, b2) - прямая общего положения; $
$ d(d1, d2) - горизонтально-проецирующая прямая $ Прямая m пересекает прямую d в точке G
$ m_{1} ∩ d_{1} = G_{1} $ Прямая m пересекает прямую d в точке G под прямым углом
$ m_{2} ∩ d_{2} = G_{2} ^ m_{2} ⊥ d_{2} $ Так как
$ m_{2} ‖ x ⇒ m - горизонтальная прямая $ Тогда
$ m_{1} ⊥ b_{1} ^ G_{1} ∈ m_{1} $ Откуда
$ m_{1} ∩ b_{1} = K_{1} $ Находим
$ K_{2} = b_{2} ∩ линия связи $ Находим
$ m_{2} ⋺ K_{2} ^ m_{2} ‖ x $ Находим
$ G_{2} = m_{2} ∩ d_{2} $ КомментарииНайти точку на прямой, равноудаленную от плоскостей проекций П1 и П2
Найти точку на прямой, равноудаленную от плоскостей проекций П1 и П2 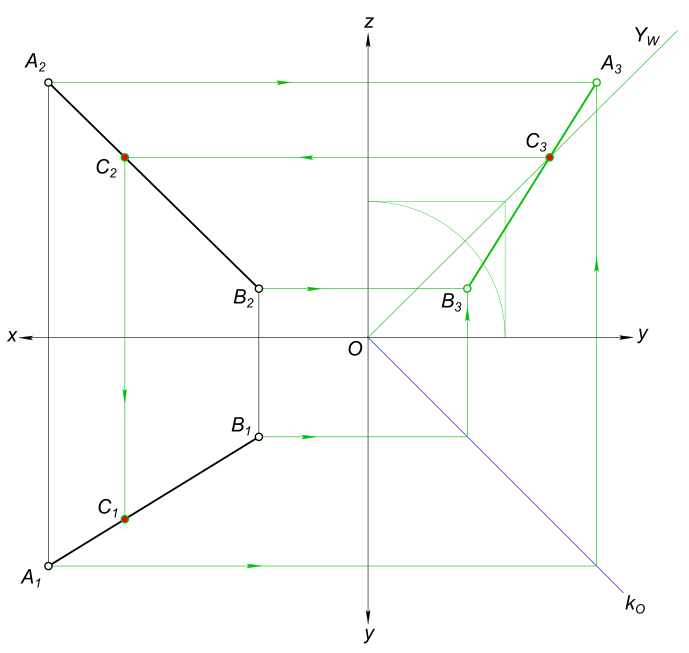
Точка на прямой, равноудаленная о плоскостей проекций Построим геометрическое место точек равноудаленных от П1 и П2
$ Фронтально-проецирующую плоскость - Y $ Находим точку встречи заданной прямой AB с плоскостью Y
$ A_{3}B_{3} ∩ Y_{3} = C_{3} $ Находим фронтальную и горизонтальную проекции точки C
$ A_{2}B_{2} ∩ линия связи = C_{2} $ и
$ A_{1}B_{1} ∩ линия связи = C_{1} $ КомментарииПостроить равносторонний треугольник ABC со стороной BC на прямой MN
Построить равносторонний треугольник ABC со стороной BC на прямой MN. Определить углы наклона высоты и плоскости треугольника к плоскостям проекций. A(105, 50, 25) M(15, 100, 70) N(155, 100, 110) 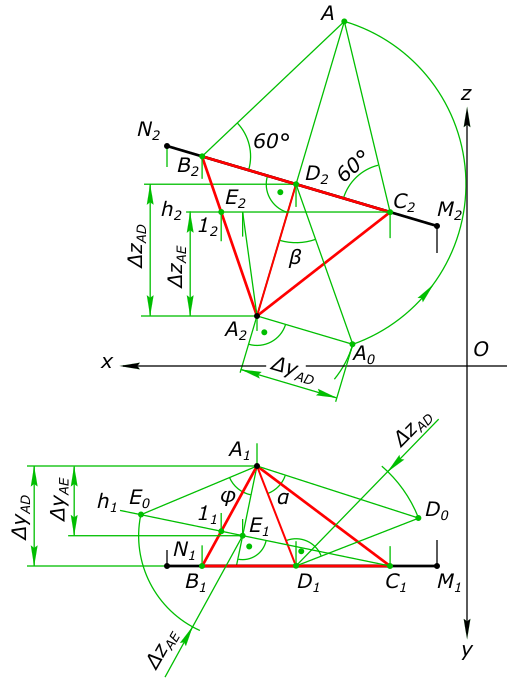
Построение равностороннего треугольника ABC со стороной BC на прямой MN Анализируя исходный чертеж
$ Прямая MN - фронталь, так как M1N1 ‖ Ox $ Откуда
$ Высота A_{2}D_{2} ⊥ M_{2}N_{2} $ Находим способом прямоугольного треугольника
$ |AD| = A_{0}D_{2} $ Строим равносторонний треугольник
$ AB_{2}C_{2} $ Получаем фронтальную и горизонтальную проекции
$ A_{2}B_{2}C_{2} и A_{1}B_{1}C_{1} $ Находим из прямоугольного треугольника A2D2A0
$ ⦟β - угол наклона высоты AD к П_{2} $ Находим из прямоугольного треугольника A1D1D0
$ ⦟α - угол наклона высоты AD к П_{1} $ Находим углы наклона плоскости треугольника ABC к плоскостям проекций: Высота AD - это в тоже время и линия ската поэтому
$ ⦟β - угол наклона ∆ABC к П_{2} $ Строим линию ската ∆ABC к П_{1} - A1E1 и из ∆A1E1E0 находиим
$ ⦟φ - угол наклона ∆ABC к П_{1} $ КомментарииПостроить проекции пинии пересечения наклонного цилиндра с половиной цилиндра
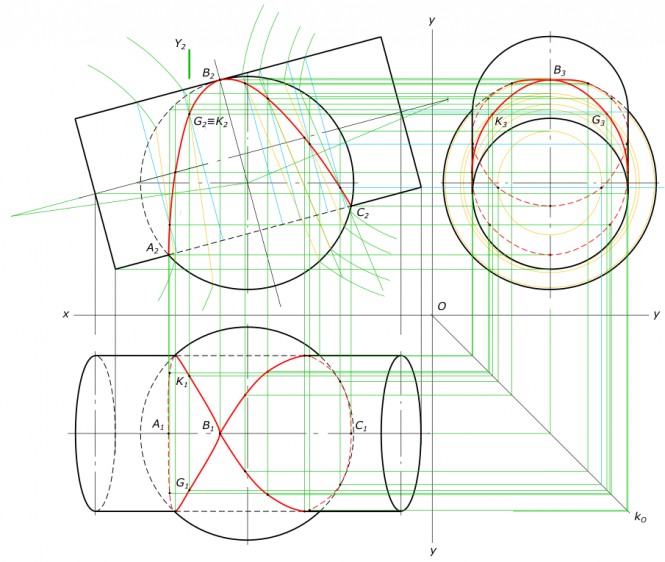
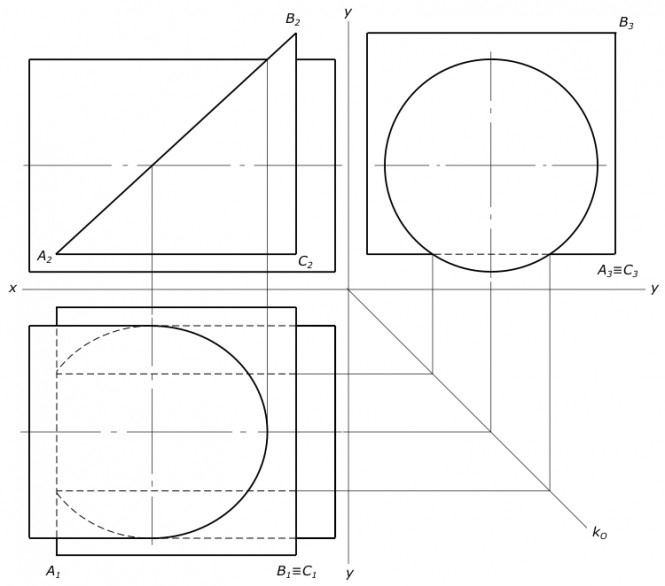
Построить проекции пинии пересечения наклонного цилиндра с половиной цилиндра Сначала, без каких-либо построений находим точки линии пересечения A, G и K Для построения промежуточных точек EF BC вводим фронтально-проецирующие вспомогательные плоскости Σ и Υ. Профильные проекции точек строим с помощью постоянной прямой Монжа kO. КомментарииПостроить проекции пинии пересечения наклонного цилиндра с половиной цилиндра
Построить проекции пинии пересечения наклонного цилиндра с половиной цилиндра КомментарииПостроить проекции линии пересечения сферы и цилиндра. Пожалуйста, очень срочно
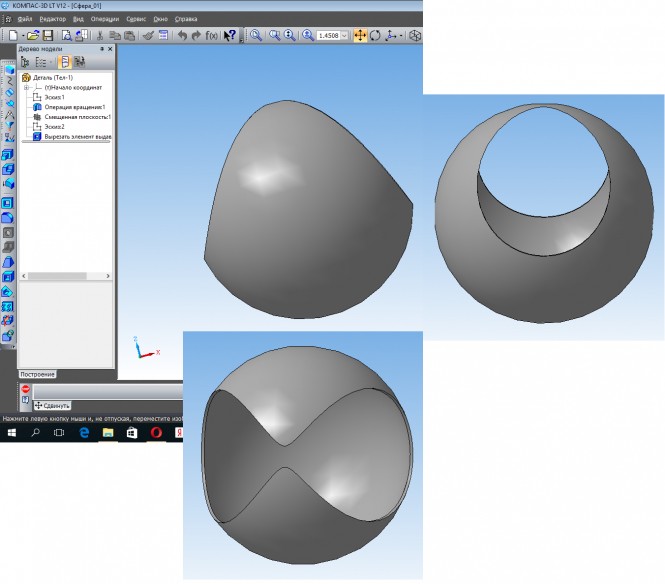
Построить проекции линии пересечения сферы и цилиндра КомментарииПостроить проекции линии пересечения сферы и цилиндра. Пожалуйста, очень срочно
Построить проекции линии пересечения сферы и цилиндра Точки A2, ..., B2, ..., C2 линии пересечения сферы и цилиндра находим способом концентричных секущих сфер. Профильные проекции точек A3, ..., B3, ..., C3 находим с помощью секущих плоскостей типа Y2. Горизонтальные проекции точек A1, ..., B1, ..., C1 находим с помощью постоянной прямой Монжа kO. Определение видимости на плоскостях проекций выполняем методом конкурирующих точек. КомментарииПостроить линию пересечения призмы с цилиндром
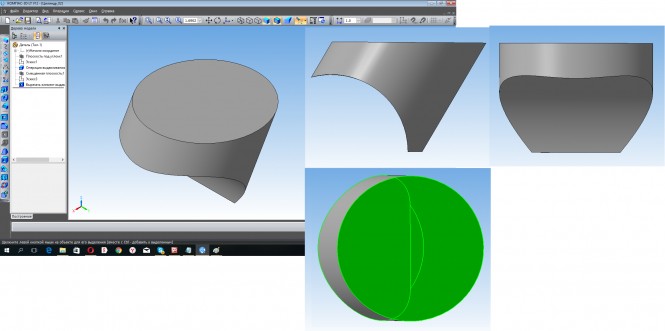
Построим линию пересечения призмы с цилиндром в КОМПАСе КомментарииПостроить линию пересечения призмы с цилиндром
Построить линию пересечения призмы с цилиндром Боковые грани призмы пересекают цилиндр: грань BC // П3 - по окружности; грань AB // П1 по образующим и грань AB - по эллипсу. Для построения профильной проекции воспользуйтесь постоянной прямой эпюра Монжа. КомментарииПостроить прямоугольный треугольник ABC у которого катет AB принадлежит прямой a, и катет AC=40, гипотенуза BC=55 и параллельна плоскости(A, b)
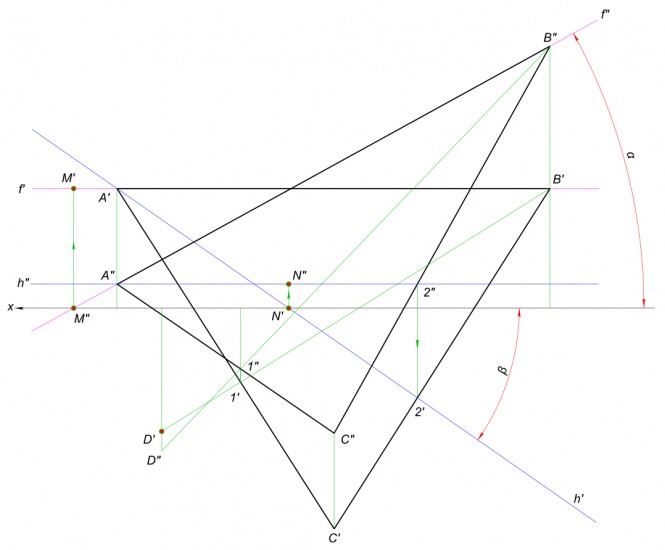
Анализ условия задачи: катеты прямоугольного треугольника
$ AB и AC значит угол при вершине A прямой $ Откуда также делаем вывод
$ вершина C ∈ β(h ∩ f = A) ⊥ a $ Способом перемены плоскостей проекций строим:
$ натуральную величину β(h_{5} ∩ f_{5} = A_{5}); $ геометрическое место точек для вершины C треугольника
$ окружность радиуса R40. $ При этом находим положение
$ вершины B_{4}, засекая его на a_{4} радиусом R=55 $ Строим проецирующее положение плоскости α(b, A) к плоскости проекций способом перемены плоскостей проекций
$ α_{7}(b_{7}, A_{7}) ⊥ П_{7} $ Находим положение гипотенузы треугольника
$ B_{7}C_{7} ‖ α_{7} $ Находим положение точек C и B на исходных проекциях
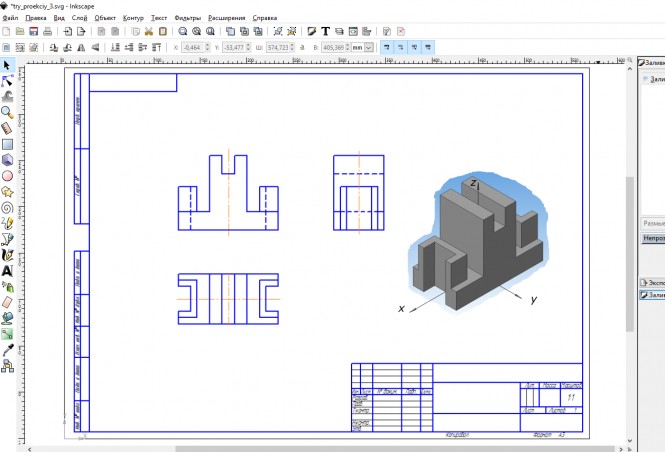
$ B(B_{1}, B_{2}) и C(C_{1}, C_{2}) $ КомментарииПостроить третий вид и аксонометрию. Толком ничего незнвю об этом. Только сегодня начинала заниматься. Помогите пожалуйста.
В программе Inkscape завершаем работу над чертежом - помещаем туда чертеж из трех видов, масштабируем его; - поверх помещаем аксонометрическую проекцию. Дорисовываем ей оси XYZ. КомментарииПостроить третий вид и аксонометрию. Толком ничего незнвю об этом. Только сегодня начинала заниматься. Помогите пожалуйста.
Пример текста КомментарииПостроить третий вид и аксонометрию. Толком ничего незнвю об этом. Только сегодня начинала заниматься. Помогите пожалуйста.
Пример текста КомментарииПостроить третий вид и аксонометрию. Толком ничего незнвю об этом. Только сегодня начинала заниматься. Помогите пожалуйста.
Пример текста Комментарии |
Записать новую задачу Все задачи Все темы Все инженеры |




Комментарии