Задачи про пересечение кривой поверхности плоскостью и прямой линией. on-line помощь репетитора. Активность в теме Пересечение кривой поверхности плоскостью и прямой линиейСамые активные инженеры в теме Пересечение кривой поверхности плоскостью и прямой линиейЛучшие решения в теме Пересечение кривой поверхности плоскостью и прямой линиейПересечение конуса плоскостью общего положения
Построить линию сечения поверхности конуса плоскостью общего положения Способом замены плоскостей проекций. Определить натуральную величину построенного сечения. Найти проекции фигуры, усеченной плоскостью и натуральную величину сечения
Построить три проекции фигуры, усеченной плоскостью и натуральную величину сечения. КомментарииСпасибо большое! Теперь стало все понятно
Найти точки пересечения поверхности цилиндра прямой линией
Пересечение прямой с поверхностью цилиндра - это задача по определению точек встречи прямой с поверхностью цилиндра. Поверхность цилиндра представляет собой поверхность вращения с образующей в виде прямой линии. 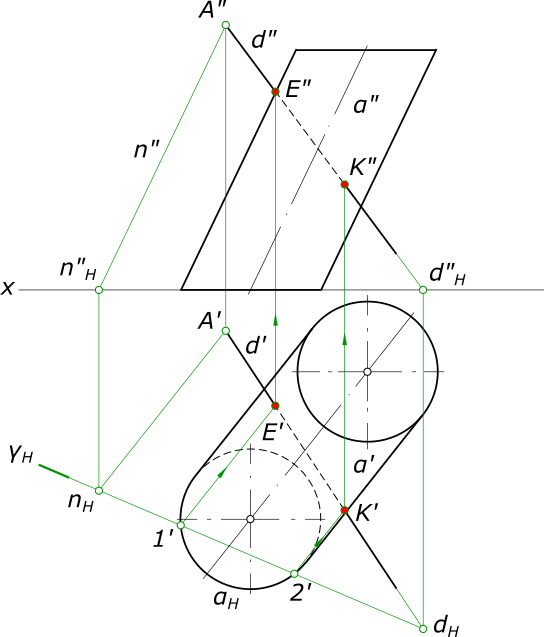
рисунок 1 Здесь прямая d занимают общее положение и поверхность цилиндра α формируется прямыми пересекающимися в несобственной точке S. Решать задачу на пересечение прямой с цилиндром следует, применяя алгоритм пересечения прямой с поверхностью: - Заключаем прямую d в вспомогательную плоскость γ, которая пересечет цилиндр по прямым линиям - образующим. Плоскость γ задаем пересечением в точке A прямой d и прямой n параллельной образующим цилиндра; - Находим точки пересечения 1 и 2 этой плоскости с основанием цилиндра, для чего строим горизонтальный след плоскости - γH по следам прямых nH и dH. - В пересечении образующих цилиндра 1 и 2 с прямой d находим искомые точки E и K пересечения прямой с поверхностью цилиндра. Пересечение прямой с поверхностью цилиндра - это также задача по определению видимости с помощью конкурирующих точек: - для горизонтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK; - для фронтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK. КомментарииМетодом секущих плоскостей построить линию пересечения поверхностей сферы и трехгранной призмы
Построить линию пересечения поверхностей призмы и сферы способом секущих плоскостей 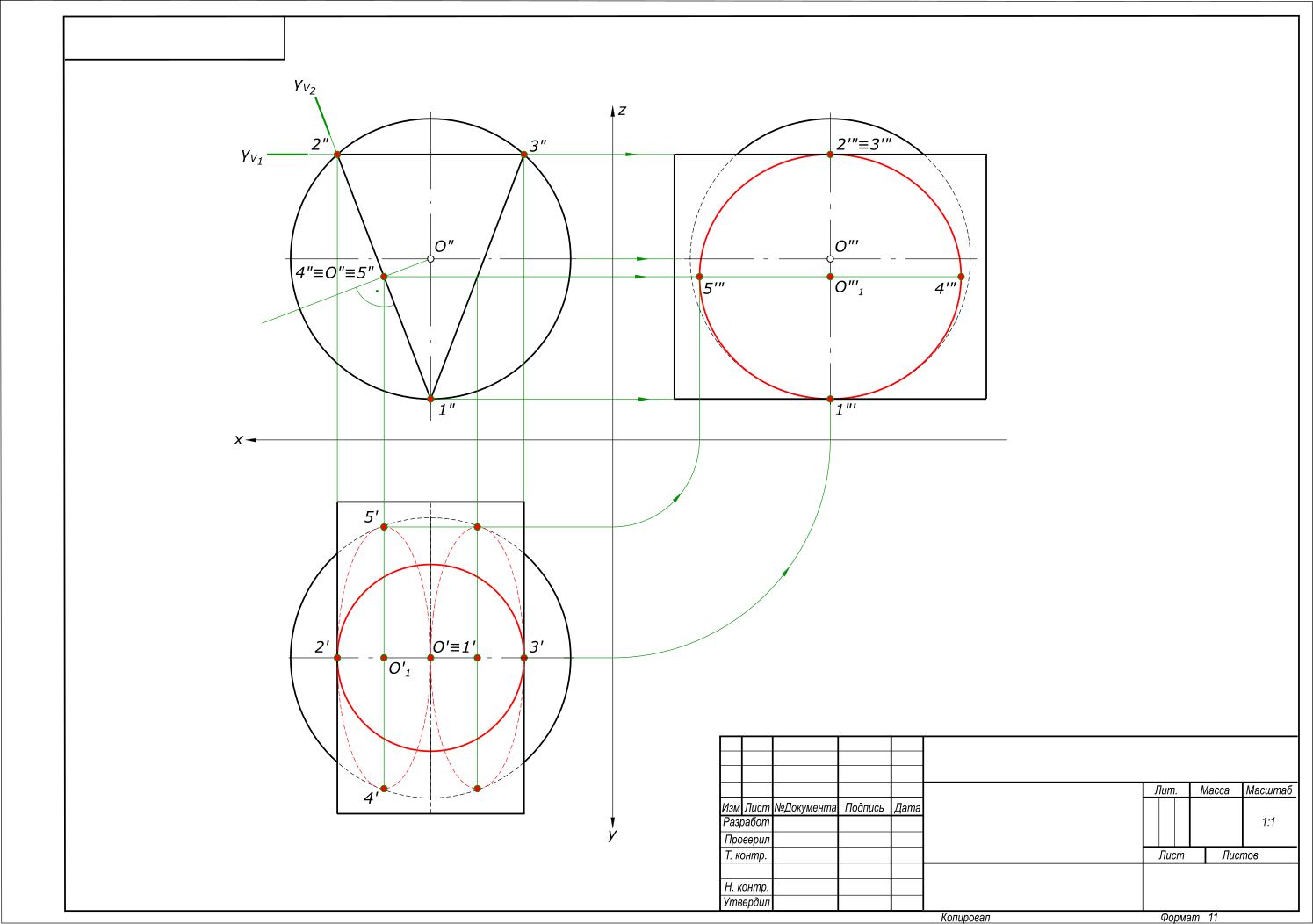
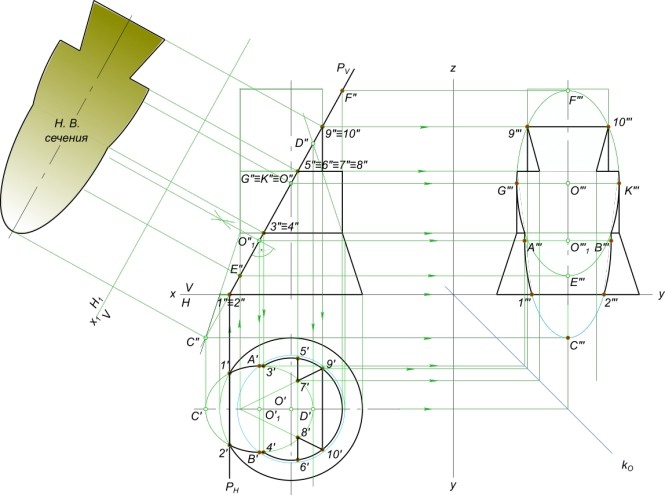
рисунок 1 Построение линии пересечения поверхностей призмы и сферы выполняем способом секущих плоскостей. На данном чертеже это плоскости γ1 и γ2. Секущая плоскость γ1 - плоскость проходящая через верхнюю грань призмы. Ее линия сечения сферы - окружность. γ1 - плоскость уровня, параллельная плоскости H, поэтому окружность проецируется на нее без искажения. Секущая плоскость γ2 - плоскость проходящая через боковую грань призмы. Ее линия сечения сферы - окружность. γ2 - фронтально проецирующая плоскость, имеет наклон к плоскостям H и W, поэтому окружность проецируется на них с искажением в виде эллипсов. Для построения эллипсов находим их центр O1 и малые 1 - 2, O - 2, O - 3 и большие оси 4 - 5. разъяснения по построению эллипсов можно найти выбрав в главном меню три точки(...) и там NGEO(начертательная геометрия). КомментарииА в итоге линии пересечения этих двух тел как будут выглядеть?
В начертательной геометрии мне известны ортогональные проекции, аксонометрическая проекция и параллельная, с итогами не встречался.
Построить прооекции точек пересечения прямой I с поверхностью
Построить проекции точек пересечения прямой I с поверхностью наклоненного цилиндра 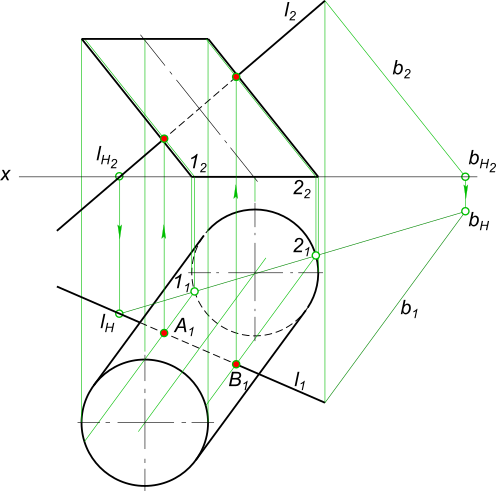
рисунок 1 КомментарииСложнейшие задачи в теме Пересечение кривой поверхности плоскостью и прямой линией Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Найти проекции фигуры, усеченной плоскостью и натуральную величину сечения Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Найти проекции фигуры, усеченной плоскостью и натуральную величину сечения
16 декабря 2016 06:43
0 подписчиков
1180 просмотров
1
решение  Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Пересечение конуса плоскостью общего положения Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Пересечение конуса плоскостью общего положения
16 декабря 2015 17:20
0 подписчиков
1842 просмотра
1
решение  Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Построить точки пересечения прямой с поверхностью вращения Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Построить точки пересечения прямой с поверхностью вращения
23 сентября 2015 15:23
0 подписчиков
1508 просмотров
1
решение  Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Построить прооекции точек пересечения прямой I с поверхностью Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Построить прооекции точек пересечения прямой I с поверхностью
20 ноября 2016 08:25
0 подписчиков
1048 просмотров
1
решение  Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Пересечение плоских фигур с поверхностью Тема задачи: Пересечение кривой поверхности плоскостью и прямой линией
Пересечение плоских фигур с поверхностью
18 декабря 2016 22:24
0 подписчиков
1058 просмотров
1
решение |
Записать новую задачу
Все задачи
Все темы
Все инженеры
Темы с решениями Точка, прямая линия и плоскость
Решений 375
Задач 318
Точка, прямая линия и плоскость
Решений 375
Задач 318
 Нет подходящей темы
Решений 327
Задач 323
Нет подходящей темы
Решений 327
Задач 323
 Разрезы
Решений 190
Задач 174
Разрезы
Решений 190
Задач 174
 Взаимное пересечение поверхностей
Решений 158
Задач 129
Взаимное пересечение поверхностей
Решений 158
Задач 129
 Чертежи деталей
Решений 152
Задач 129
Чертежи деталей
Решений 152
Задач 129
 Построение аксонометрических изображений
Решений 132
Задач 91
Построение аксонометрических изображений
Решений 132
Задач 91
|



Комментарии