Методом секущих плоскостей построить линию пересечения поверхностей сферы и трехгранной призмы

Создано: @nick 28 декабря 2015 10:06

поставьте оценку:

1 голосов, средний бал: 5.0000

Построить линию пересечения поверхностей призмы и сферы способом секущих плоскостей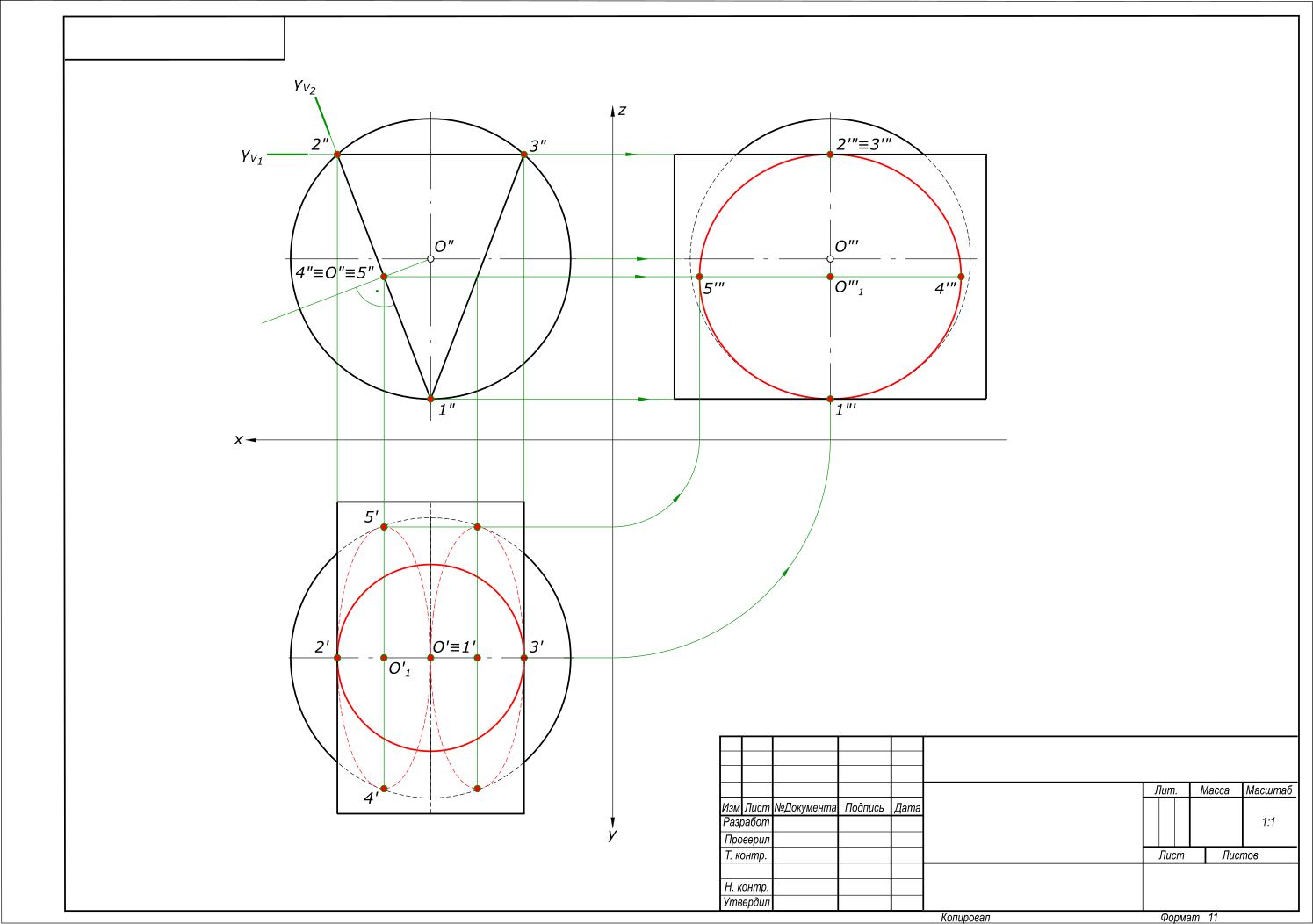

рисунок 1

Построение линии пересечения поверхностей призмы и сферы выполняем способом секущих плоскостей. На данном чертеже это плоскости γ1 и γ2.

Секущая плоскость γ1 - плоскость проходящая через верхнюю грань призмы. Ее линия сечения сферы - окружность. γ1 - плоскость уровня, параллельная плоскости H, поэтому окружность проецируется на нее без искажения.

Секущая плоскость γ2 - плоскость проходящая через боковую грань призмы. Ее линия сечения сферы - окружность. γ2 - фронтально проецирующая плоскость, имеет наклон к плоскостям H и W, поэтому окружность проецируется на них с искажением в виде эллипсов.

Для построения эллипсов находим их центр O1 и малые 1 - 2, O - 2, O - 3 и большие оси 4 - 5.

разъяснения по построению эллипсов можно найти выбрав в главном меню три точки(...) и там NGEO(начертательная геометрия).