Задачи про взаимное пересечение прямой, плоскости и поверхности. on-line помощь репетитора. Активность в теме Взаимное пересечение прямой, плоскости и поверхностиСамые активные инженеры в теме Взаимное пересечение прямой, плоскости и поверхностиЛучшие решения в теме Взаимное пересечение прямой, плоскости и поверхностиНайти точку пересечения прямой с плоскостью
1) Проводим через прямую горизонтально-проецирующую плоскостьγ и отмечаем точки ее пересечения со сторонами треугольника. Точка пересечения стороны 2—3 на фронтальной плоскости проекций не определяется ввиду ее профильного положения. Заменив в плоскости треугольника сторону 2—3 на прямую общего положения 2—5, определяем вторую точку 6 линии пересечения плоскостей 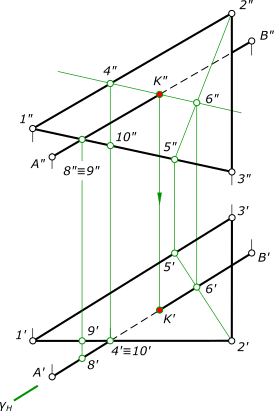
рисунок 1 2) Определяем в пересечении прямой AB и линии пересечения плоскостей 4—6 искомую точку K встречи прямой с плоскостью треугольника. 3) Определяем видимость прямой: a) на горизонтальной плоскости проекций: отмечаем конкурирующие точки 4 и 10, принадлежащие стороне 1—2 треугольника и прямой AB соответственно. Точка 4 удалена от плоскости H, более чем точка 10 значит прямая до точки пересечения K с плоскостью треугольника будет невидима; b) на фронтальной плоскости проекций: отмечаем конкурирующие точки 8 и 9, принадлежащие прямой AB и стороне 1—3 треугольника соответственно. Точка 8 удалена от плоскости V, более чем точка 9 значит прямая до точки пересечения K с плоскостью треугольника будет видима. Построить проекции шара, касающегося отрезка АВ, с центром в точке С. А(75,10,25); В(5,10,55); С(35, 30,30).
Построить проекции шара, касающегося отрезка АВ, с центром в точке С. А(75,10,25); В(5,10,55); С(35, 30,30). 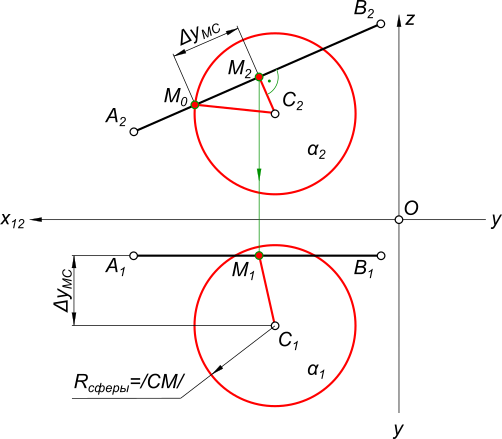
Построение проекций шара Представим в пространстве сферу α ее касается некая плоскость в точке M. Радиус сферы проведенный в точку касания перпендикулярен всем прямым плоскости в том числе и отрезку AB, который по условию задачи касается сферы и значит пересекается с этим радиусом. Итак радиус сферы и отрезок AB - пересекающиеся под прямым углом прямые ... Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи получаем: Горизонтальная проекция отрезка AB параллельна оси X, откуда следует, что данный отрезок параллелен фронтальной плоскости проекций
$ A_{1}B_{1} ‖ Ox ⇔ AB ‖ П_{2} $ Исходя из теоремы о проецировании прямого угла
$ CM ⊥ AB ⇔ C_{2}M_{2} ⊥ A_{2}B_{2} $ Точка M принадлежит прямой AB, следовательно ее проекции лежат на одноименных проекциях прямой. Справедливо и обратное утверждение: проекции точки M лежат на одноименных проекциях прямой AB, следовательно, точка принадлежит этой прямой
$ M ∈ AB ⇔ M_{2} ∈ A_{2}B_{2}, M_{1} ∈ A_{1}B_{1} $ Построив проекции отрезка CM находим его натуральную величину способом прямоугольного треугольника. КомментарииПостроить линию пересечения плоских фигур . Показать видимость
Построить линию пересечения плоских фигур . Определить видимость 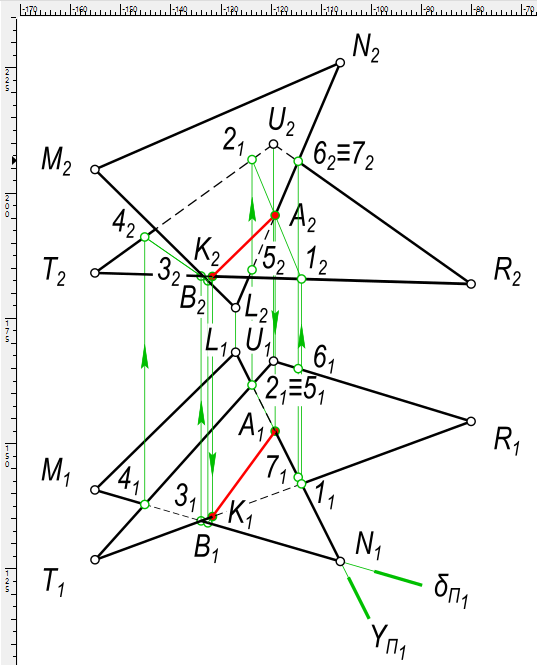
рисунок 1 КомментарииПостроить три вида данного геометрического тела и выполнить фронтальный и профильный разрезы.
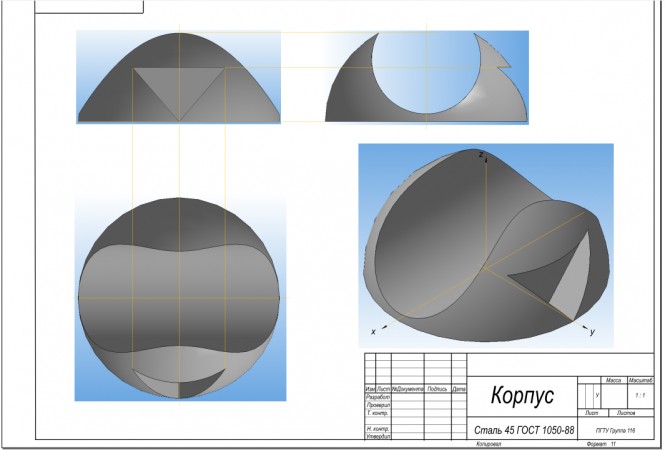
Построить три вида данного геометрического тела (вырезы в пирамиде) и выполнить фронтальный и профильный разрезы 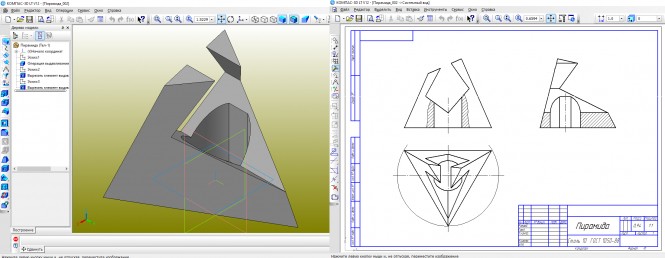
Построить три вида данного геометрического тела (вырезы в пирамиде) и выполнить фронтальный и профильный разрезы КомментарииПостроить линию пересечения
Построить линию пересечения поверхностей сферы, цилиндра и призмы КомментарииСложнейшие задачи в теме Взаимное пересечение прямой, плоскости и поверхности Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Найти точку пересечения прямой с плоскостью Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Найти точку пересечения прямой с плоскостью
14 сентября 2015 14:51
0 подписчиков
2972 просмотра
1
решение  Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Через т А провести перпендикуляр к плокости Р (АВС) Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Через т А провести перпендикуляр к плокости Р (АВС)
21 января 2016 13:43
0 подписчиков
1398 просмотров
1
решение  Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Построить три проекции пирамиды с вырезом и ее развертку Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Построить три проекции пирамиды с вырезом и ее развертку
25 февраля 2016 23:44
0 подписчиков
13374 просмотра
1
решение  Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Относительное положение поверхностей. Способ секущих плоскостей Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Относительное положение поверхностей. Способ секущих плоскостей
30 ноября 2016 08:39
0 подписчиков
1588 просмотров
1
решение  Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Способом замены плоскостей построить сечение плоскостью общего положения и натуральную величину сечения Тема задачи: Взаимное пересечение прямой, плоскости и поверхности
Способом замены плоскостей построить сечение плоскостью общего положения и натуральную величину сечения
7 января 2016 12:41
0 подписчиков
2905 просмотров
7
решений |
Записать новую задачу
Все задачи
Все темы
Все инженеры
Темы с решениями Точка, прямая линия и плоскость
Решений 398
Задач 346
Точка, прямая линия и плоскость
Решений 398
Задач 346
 Нет подходящей темы
Решений 309
Задач 307
Нет подходящей темы
Решений 309
Задач 307
 Разрезы
Решений 192
Задач 176
Разрезы
Решений 192
Задач 176
 Чертежи деталей
Решений 156
Задач 134
Чертежи деталей
Решений 156
Задач 134
 Взаимное пересечение поверхностей
Решений 154
Задач 130
Взаимное пересечение поверхностей
Решений 154
Задач 130
 Построение аксонометрических изображений
Решений 128
Задач 92
Построение аксонометрических изображений
Решений 128
Задач 92
|



Комментарии