провести через точку с,плоскость а перпендикулярную отрезку ав. задать плоскость пересекающимися прямыми Тема задачи: Точка, прямая линия и плоскость
Тема задачи: Точка, прямая линия и плоскость
 Создано:
@regi
15 декабря 2022
20:21
Создано:
@regi
15 декабря 2022
20:21
провести через точку с,плоскость а перпендикулярную отрезку ав. задать плоскость пересекающимися прямыми Решения задачиПример текста КомментарииВот, теперь прямые а и b проведены верно. Запишем пояснения правильно. Например С ∈ b ⇔ C1 ∈ b1, C2 ∈ b2. Что означает - Точка С принадлежит прямой b, значит проекция С1 принадлежит b1 и проекция С2 принадлежит b2.
Ураааа!Спасибоооооо!!!а то,что я писала рядом с чертежом можно оставить?и то,что вы написали дополню
И ещё такой вопрос:те прямые,которые параллельны АВ оставить без обозначения?
И вообще на чертеже нужно что то добавить из обозначений?или оставить все в таком виде?
И наоборот.
Провести через точку С плоскость α перпендикулярную отрезку АВ. Задать плоскость пересекающимися прямыми 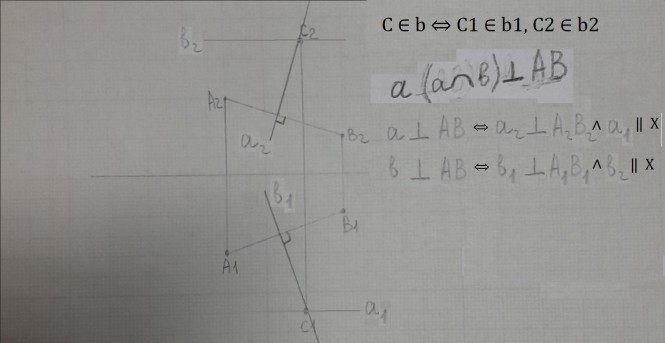
Провести через точку С плоскость α перпендикулярную отрезку АВ. Задать плоскость пересекающимися прямыми КомментарииПример текста КомментарииТак должно выглядеть построение данной задачи или нужно чтт то дополнить?
В ходе построений принято делать на чертеже обозначения.
Вы имеете ввиду обозначения прямых,которые я провела из точек С2 и С1?
Да. И что это за прямые?
Проведём перпендикулярные прямые горизонтальной и фронтальной проекций из точек С1 и С2.Получим....
Вы не дали обозначение того что сделали на чертеже. А, какое условие перпендикулярности двух прямых?
Не пойму никак как обозначить их.условие перпендикулярности такое,что если при пересечении двух прямых один угол равен 90 градусах то и остальные 3 уола будут равны 90 градусам...а дальше что,подскажите,пожалуйста,что я ещё должна обозначить на этом чертеже?
Вы не дали обозначение того что сделали на чертеже - провели прямую или провели прямые через точку С. Наберите в поисковой строке сайта - условие перпендикулярности прямой плоскости, -условие перпендикулярности прямой
Я смотрела,там 3 задачи,которые для меня кажутся очень сложными...и я не понимаю,к сожалению.Может быть приведете пример чертежа более подходящий к моему, пожалуйста?
Пример текста КомментарииВот что получилось у меня.. . Поясните пожалуйста.
Из точки С2 получилась точка 1 штрих.из точки С1 провела перпендикуляр он пересекает ось Х,показываю его штрих пунктиром,так как он перекрывается фронтальной плоскость.Что дальше не знаю,помогите,пожалуйста
А, вас просили обозначить проведенные прямые.
Пример текста КомментарииПоясните пожалуйста. И где здесь обозначение ваших прямых.
А, имена у этих прямых имеются. Прямую АВ вы назвали - а.
Я совсем запуталась...
Допустим вы следовали моим рекомендациям и набрали в поисковой строке ... . Смотрите картинку в моем решении.
Да да,я увидела
Как много вы сообщили в своем комментарии, однако. Что вы думаете о прямых h и f в этой задаче поясните пожалуйста.
Я вижу что они перпендикулярны с D,так?
Тут вы утверждаете, что они перпендикулярны с точкой D. Как прямая может быть перпендикулярна точке. Вероятно вы имели в виду что прямые h и f перпендикулярны к AD и n.
И ещё я так понимаю,это произвольные прямые? А точки пересечения опускаем на горизонтальную плоскость
Точки пересечения прямых h и f с линиями треугольника и сам треугольник мысленно выбрасываем из данной задачи для того чтобы получить вашу задачу. Поясните, пожалуйста, почему по вашему прямые h и f - произвольные прямые?
Пример текста КомментарииНа эпюре может быть прямая a, прямая b? По моему прямая a и прямая b находятся в пространстве.
Пример текста Комментарии Я же спрашивал где a1, a2, b1, b2, а не A1, A2, B1, B2.
Пример текста КомментарииКажется я просил давать к картинкам (решениям) пояснения, будьте любезны.
Точка С задана на чертеже горизонтальной и фронтальной проекция ?ми С(С1,С2)
Точка С2 принадлежит прямой в2,точка С1 принадлежит прямой в1
Точка С2 фронтальной проекции совпадает с точкой С1 горизонтальной проекции
Правильно?что ещё можно добавить?
Добавить необходимо: условие перпендикулярности прямой плоскости; какие прямые подойдут наилучшим образом для задания плоскости; теорему о проецировании прямого угла.
Если прямая перпендикулярна двум пересекающимся прямым в плоскости,то она перпендикулярна этой плоскости,верно?теперь нужно на чертеже обозначить это условие?
Прямые а1 и а2 наилучшим образом подойдут для задания плоскости
Нет прямых а1 и а2, есть проекции прямой а - а1 и а2.
Тогда так.проекции прямой а а1 и а2,и проекции прямой в в1 и в2,верно?
Еще раз посмотрите мое решение и найдите там теорему о проецировании прямого угла. Затем необходимо правильно провести указанные прямые. а(а1, а2) и b(b1, b2)
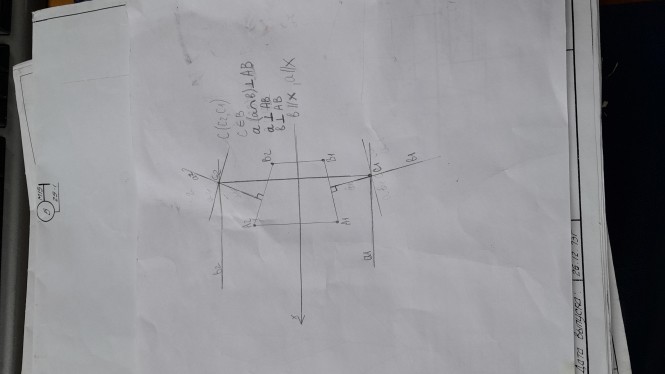
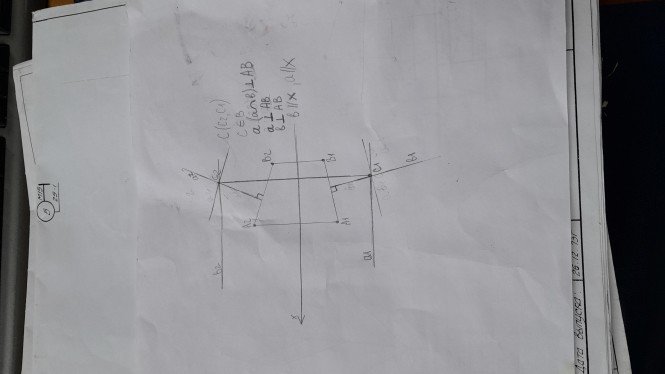
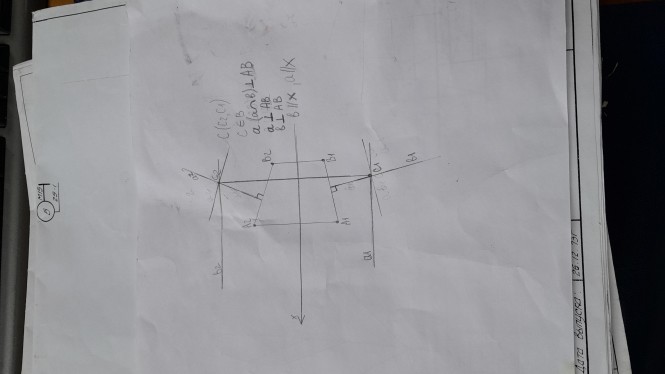
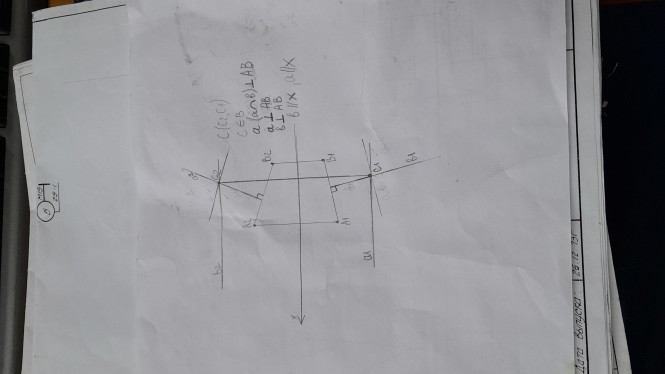
Пример текста КомментарииНа представленном чертеже нет прямой а, и писать что а ⊥ А2В2 и а ⊥ А1В1 нельзя. Запись С2 ≡ С1 означает совпадение проекций, этого на чертеже нет.
Пример текста Провести через точку С плоскость α перпендикулярную отрезку АВ. Задать плоскость пересекающимися прямыми. Ход выполнения данной задачи: 1. Выяснить условие перпендикулярности прямой плоскости; 2. Выяснить какие прямые подойдут наилучшим образом для задания плоскости; 3. Выполнить построения. 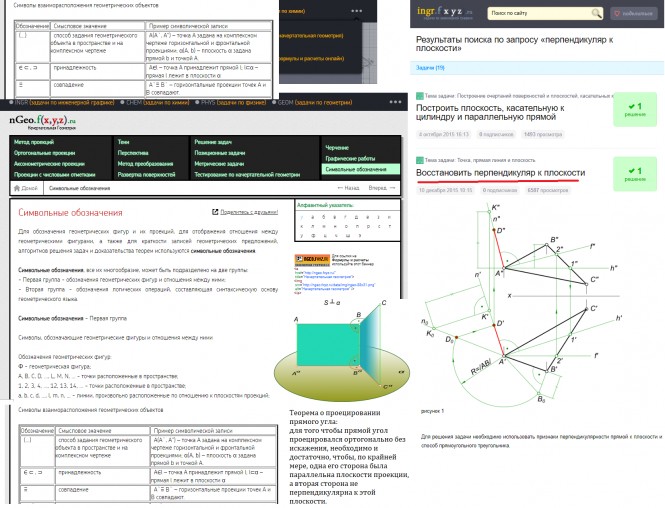
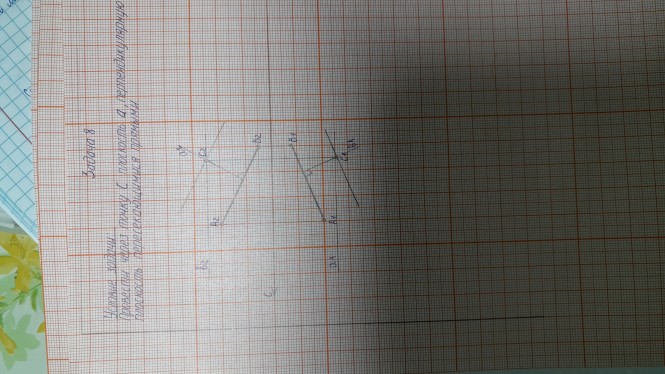
Провести через точку С плоскость α перпендикулярную отрезку АВ. Задать плоскость пересекающимися прямыми На рисунке к теореме о проецировании прямого угла изображено две взаимноперпендикулярные прямые. Одна из прямых произвольного положения, а другая частного (параллельна) плоскости проекций. Прямая общего положения имеет на чертеже проекции не параллельные оси Х. Прямая частного положения имеет одну проекцию параллельную оси Х, а другую проекцию непараллельной оси Х. КомментарииА чертёж сможете показать?
Пожалуйста,помогите выполнить построение данной задачи. Заранее спасибо
На рисунке к теореме о проецировании прямого угла изображено две взаимноперпендикулярные прямые. Одна из прямых произвольного положения, а другая частного (параллельна) плоскости проекций. Прямая общего положения имеет на чертеже проекции не параллельные оси Х. Прямая частного положения имеет одну проекцию параллельную оси Х, а другую проекцию непараллельной оси Х.
Пример текста КомментарииМожно наверное ещё добавить утверждение С принадлежит прямой а
Да, можно. а ⊥ АВ ? A, что требуется?
Требуется пояснить что я сделала?
Пример текста КомментарииКажется я просил давать к картинкам (решениям) пояснения, будьте любезны.
Точка С задана на чертеже горизонтальной и фронтальной проекциями С1,С2.2)точка С принадлежит прямой В;3)плоскость а перпендикулярна АВ;4)плоскость в перпендикулярна АВ;5) прямая в параллельная АВ
Верно?
Плоскость α(а ∩ b) ⊥ AB - принимается. А, чем задана плоскость b? Прямая b ‖ AB - Верно, только для чего это?
Плоскость в нужно задать другими прямыми?к примеру прямой с и d?
Мы выяснили условие перпендикулярности прямой к плоскости так ведь?
Все поняла.нам по условию нужно плоскость а. Про плоскость в речи не идет
Правильно.
Теперь мне нужно все это описать пошагово..поможете?
Плоскость альфа (α) задана двумя пересекающимися прямыми перпендикулярна прямой AB. А, какое условие перпендикулярности прямой плоскости?
Значит АВ ппрпендикулярна прямым а и в, то АВ перпендикулярна плоскости альфа
Ну, теперь осталось изобразить на чертеже: а ⊥ АВ и b ⊥ AB. Используя теорему о проецировании прямого угла.
Пример текста КомментарииНа рисунке к теореме о проецировании прямого угла изображено две взаимноперпендикулярные прямые. Одна из прямых произвольного положения, а другая частного (параллельна) плоскости проекций. Прямая общего положения имеет на чертеже проекции не параллельные оси Х. Прямая частного положения имеет одну проекцию параллельную оси Х, а другую проекцию непараллельной оси Х.
Произвольного положения это перпендикуляр?а частная это прямые параллельные АВ?
Где проекции а1, а2 и b1? b2?
Думаю ещё нужно начертить прямые,параллельные оси Х через точку С.а1 и в1 будут в горизонтальной проекции,а а2 и в2 во фронтальной проекции,так ведь?
А, не пора начертить чертеж и дать пояснения к нему? Уж кажется все ясно,
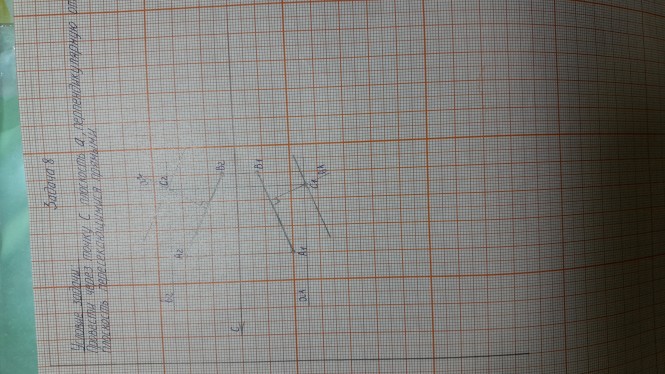
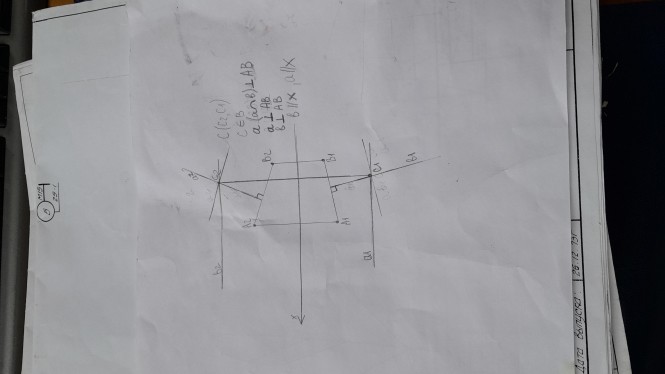
Пример текста КомментарииНеправильно, однако, у вас прогресс, на чертеже появились проекции прямых . Прямая АВ общего положения, а прямые а и b частного перпендикулярные АВ.
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии