На рисунке 6.3 изображены плоские сечения. Вычертить сечение в масштабе. Определить координаты его центра тяжести. Показать на ч
Тема задачи: Нет подходящей темы
Создано:
@zhan
7 мая 2021
18:14
На рисунке 6.3 изображены плоские сечения. Вычертить сечение в масштабе. Определить координаты его центра тяжести. Показать на чертеже центр тяжести сечения. текста 
рисунок 1 Решения задачиОпределить координаты центра тяжести плоской фигуры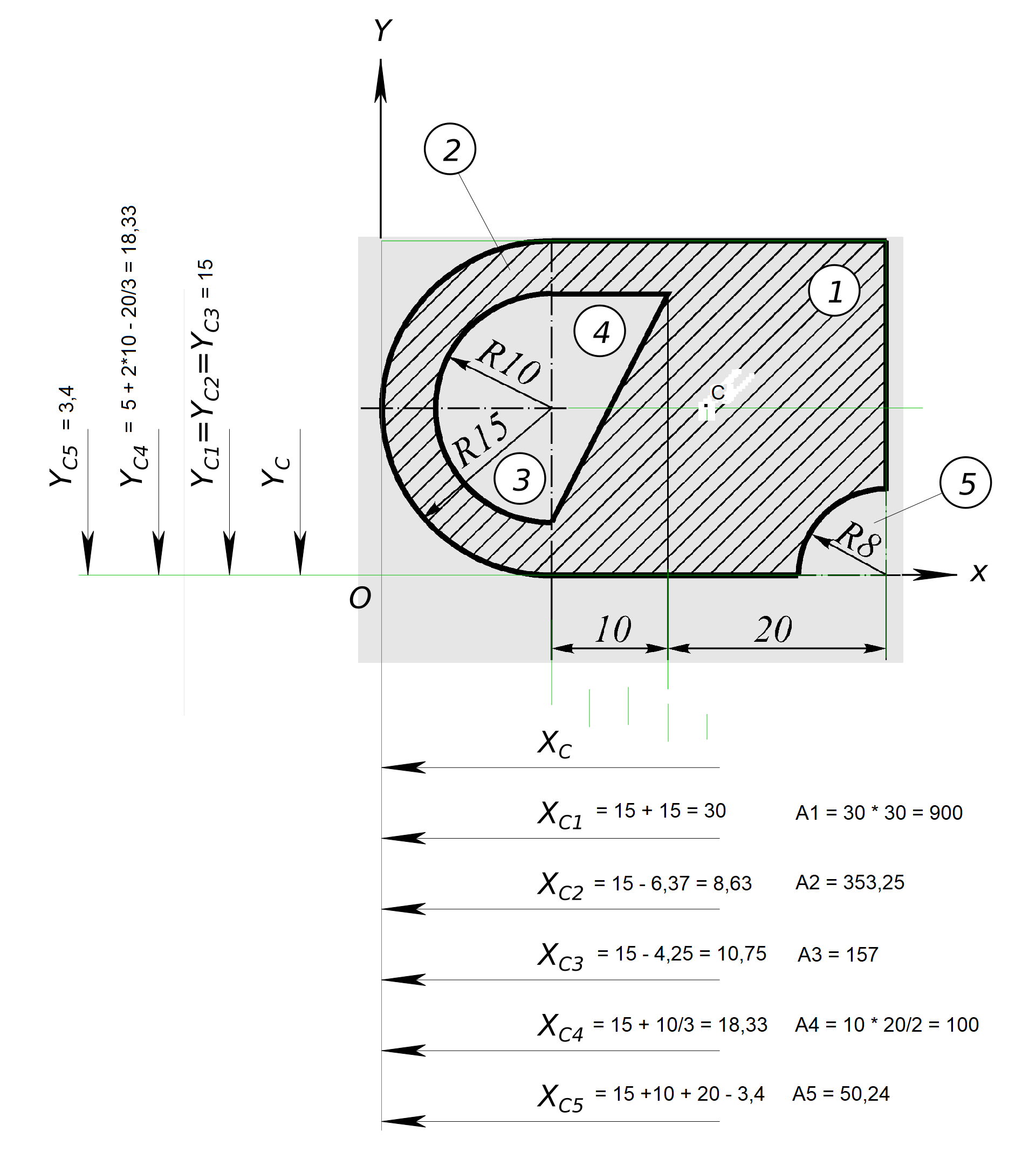 
Определить координаты центра тяжести плоской фигуры Расчетно графическую работу выполняем по следующему алгоритму: - выбираем рациональное направление осей X и Y. Данная плоская фигура не имеет осей симметрии, поэтому ось X проводим по основанию (нижней границе) фигуры и ось Y - по крайней левой точке (границе); - разбиваем сложную фигуру на простые: 1 - прямоугольник, 2 - большой полукруг, 3 - малый полукруг, 4 - треугольник, 5 - сектор круга. 1 - прямоугольник со сторонами 2*15 и 10 + 20
$ X_{C_{1}} = 15 + \frac{10+20}{2} = 30 мм $ 2 - большой полукруг
$ X_{C_{2}} = 15 - \frac{4R}{3π} = 15 - \frac{4*15}{3π} = 8,63 мм $ Площадь
$ A_{2} = \frac{π}{2}*R*R = 353,25 мм^{2} $ 3 - малый полукруг
$ X_{C_{3}} = 15 - 4*R/(3*π) = 15 - \frac{4*10}{3*π} = 10,75 мм $ Площадь
$ A_{3} = \frac{π}{2}*R^{2} = \frac{π}{2}*10^{2} = 157 мм^{2} $ 4 - треугольник
$ X_{C_{4}} = 15 + \frac{10}{3} = 18,33 мм $ Площадь
$ A_{4} = 10\frac{20}{2} = 100 мм^{2} $ 5 - круговой сектор
$ X_{C_{5}} = 15 + 10 + 20 - 3,4 = 41,6 мм $ Площадь
$ A_{5} = \frac{πR^{2}}{4} = \frac{π8^{2}}{4} = 50,24 мм^{2} $ - Определяем координаты центра тяжести плоской фигуры
$ X_{C} = \frac{ΣA_{i}X_{i}}{ΣA_{i}}= $
$ = \frac{900×30+353,25×8,63-157×10,75}{900+353,25-157-100-50,24}+ $
$ +\frac{-100×18,33-50,24×41,6}{900+353,25-157-100-50,24}=27,86 мм $
$ Y_{C} = \frac{ΣA_{i}Y_{i}}{ΣA_{i}}= $
$=\frac{900×15+353,25×15-157×15}{900+353,25-157-100-50,24}+$
$ +\frac{-100×18,33-50,24×3,4}{900+353,25-157-100-50,24}= 15,26 мм $ - Отмечаем положение центра тяжести фигуры на чертеже КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии