Определить размеры поперечного сечения балки

Создано: @nick 2 февраля 2020 12:37

Определить размеры поперечного сечения балки из условия прочности. Если известны наибольший изгибающий момент равный 0,54 кН×мм, что соотношение сторон прямоугольного сечения b/h = 0,6. [σ]=100 МПа

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 2 февраля 2020 13:24

поставьте оценку:

0 голосов, средний бал: 0.0000

Определить размеры поперечного сечения балки

Запишем условие прочности при изгибе

$ [σ] ≥ \frac{M_{x}}{W_{x}} $

Откуда

$ W_{x} ≥ \frac{M_{x}}{[σ]} $

Момент сопротивления прямоугольного сечения определяется по формуле

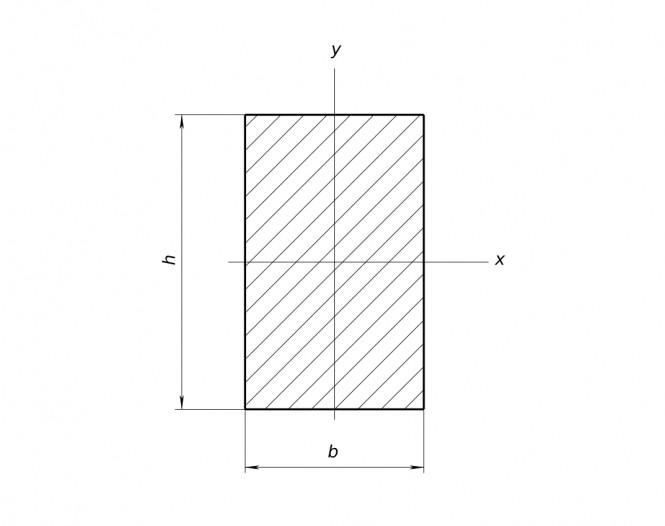
$ W_{x} = \frac{J_{x}}{y_{max}} = \frac{\frac{bh^{3}}{12}}{\frac{h}{2}}=\frac{bh^{2}}{6} $

Переписываем условие прочности

$ \frac{bh^{2}}{6} ≥ \frac{M_{x}}{[σ]} $

Соотношение сторон прямоугольного сечения

$ \frac{b}{h} = 0,6 $

Откуда

$ b = 0,6h $

Еще раз переписываем условие прочности

$ \frac{0,6h^{3}}{6} ≥ \frac{M_{x}}{[σ]} $

Откуда находим высоту сечения

$ h ≥ (\frac{10M_{x}}{[σ]})^{\frac{1}{3}} = (\frac{10×0,54×10^{3}}}{100})^{\frac{1}{3}}= 3,78 мм $

и ширину сечения

$ b ≥ 0,6h =0,6×3,78 = 2,27 мм $

Определить размеры поперечного сечения балки

Комментарии

Решения задачи

Комментарии