Потенциальная энергия деформации при прямом чистом изгибе

Создано: @nick 17 июля 2019 07:52

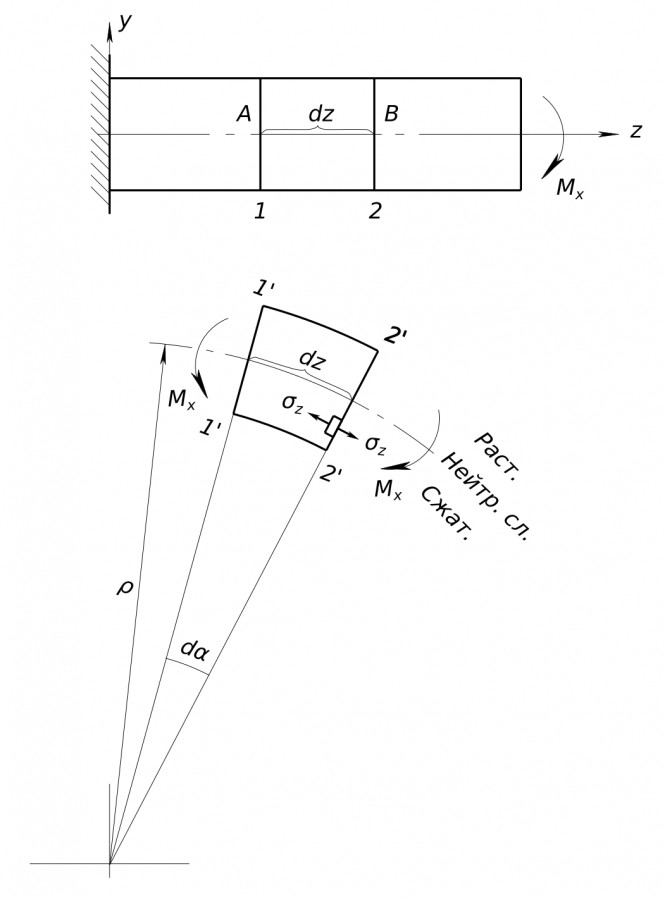
Необходимо найти потенциальную энергию упругого деформирования накопленную в балке. Считаем, что при упругом деформировании потенциальная энергия равна работе внутренних сил на перемещение точек сечений. Возьмем два плоских поперечных сечения 1 - 1 и 2 - 2. Согласно гипотезе плоских сечений, используемой при изгибе, данные сечения остануться перпендикулярными оси балки. Предполагаем, что ось балки изгибается по дуге окружности. Нейтральный слой при этом не сжимается и не растягивается.

Тогда

$ dz=ρdα $

Работа внутреннего изгибающего момента по перемещению сечения 2 - 2 относительно сечения 1 - 1 равна произведению силового фактора на перемещение

$ dU=\frac{1}{2}M_{x}dα=\frac{1}{2}M_{x}\frac{dz}{ρ}=\frac{1}{2}M_{x}\frac{1}{ρ}dz= $

$ =\frac{1}{2}M_{x}\frac{M_{x}}{EJ_{x}}dz=\frac{M_{x}^{2}}{2EJ_{x}}dz $

Таким образом потенциальная энергия деформации при прямом чистом изгибе равна

$ U=\int\from{ℓ}\frac{M_{x}^{2}}{2EJ_{x}}dz $

сложенной по ее длине потенциальной энергии перемещения элементарных участков длиной dz.

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 17 января 2024 16:34

поставьте оценку:

0 голосов, средний бал: 0.0000

Потенциальная энергия деформации при прямом чистом изгибе

Потенциальная энергия деформации при прямом чистом изгибе

Комментарии

Решения задачи

Комментарии