Изменение осевых моментов инерции при повороте осей координат Создано:
@nick
25 марта 2019
08:20
Создано:
@nick
25 марта 2019
08:20
Изменение осевых моментов инерции при повороте осей координат 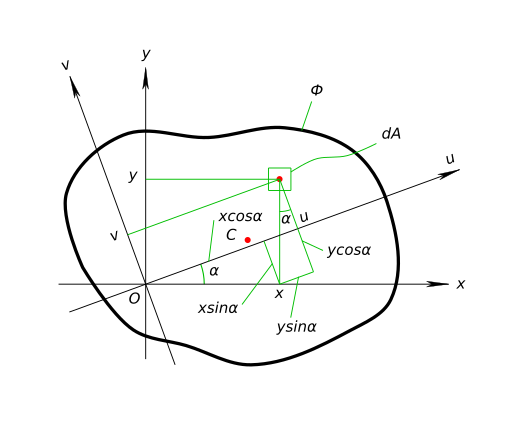
Изменение осевых моментов инерции при повороте осей координат Дана плоская фигура ...
$ Ф $ A - площадь ...
$ A=\int\from{Ф}dA, м^{2} $ Мы знаем ее осевые моменты инерции и центробежный момент инерции относительно осей xOy ...
$ J_{x}, J_{y}, J_{xy} $ Чтобы, вычислить осевые моменты инерции и центробежный момент инерции относительно осей другой системы координат uOv ...
$ J_{u}, J_{v}, J_{uv} $ повернутых на угол ...
$ α $ Необходимо связать координаты двух систем. Координата ...
$ u=xcosα+ysinα $ Координата ...
$ v=-xsinα+ycosα $ Тогда момент инерции относительно оси u
$ J_{u}=\int\from{Ф} v^{2}dA=\int\from{Ф} (-xsinα+ycosα)^{2}dA= $
$ =\int\from{Ф} (x^{2}sin^{2}α-xy2sinαcosα+y^{2}cos^{2}α)dA= $
$ =sin^{2}α\int\from{Ф} x^{2}dA-2sinαcosα\int\from{Ф}xydA+cos^{2}α\int\from{Ф}y^{2}dA= $
$ =J_{y}sin^{2}α-sin(2α)J_{xy}+J_{x}cos^{2}α $ Тогда момент инерции относительно оси v
$ J_{v}=\int\from{Ф} u^{2}dA=\int\from{Ф}(xcosα+ysinα)^{2}dA= $
$ =\int\from{Ф}(x^{2}cos^{2}α+xy2sinαcosα+y^{2}sin^{2}α^{2})dA= $
$ =cos^{2}α\int\from{Ф}x^{2}dA+2sinαcosα\int\from{Ф}xydA+sin^{2}α^{2}\int\from{Ф}y^{2}dA= $
$ = J_{y}cos^{2}α+J_{xy}sin(2α)+J_{x}sin^{2}α $ Тогда центробежный момент инерции относительно осей uv
$ J_{uv}=\int\from{Ф}uvdA=\int\from{Ф}(xcosα+ysinα)(-xsinα+ycosα)dA= $
$ =\int\from{Ф}(-x^{2}sinαcosα+xycos^{2}α-xysin^{2}α+y^{2}sinαcosα)dA= $
$ =-J_{y}\frac{sin(2α)}{2}+J_{xy}cos(2α)+J_{x}\frac{sin(2α)}{2}= $
$ =J_{xy}cos(2α)+\frac{J_{x}-J_{y}}{2}sin(2α) $ Посмотрим при каких значении угла α моменты инерции принимают экстремальные значения
$ \frac{dJ_{u}}{dα}=J_{x}2cosα+J_{y}2sinαcosα-J_{xy}2cos(2α)= $
$ =-J_{x}sin(2α)+J_{y}sin(2α)-2J_{xy}cos(2α) $
$ α_{0}⇒=0=-J_{x}sin(2α_{0})+J_{y}sin(2α_{0})-2J_{xy}cos(2α_{0})= $ Откуда
$ sin(2α_{0})(J_{y}-J_{x}=2J_{xy}cos(2α_{0}) $ Тогда
$ tg(2α_{0})=\frac{2J_{xy}}{J_{y}-J_{x}}⇒ α_{0}; J_{u}=min; max; J_{v}=max; min $ Полярный момент инерции
$ J_{u}+J_{v} = J_{ρ} $
$ J_{uv}(α^{∾})=0=J_{xy}cos(2α^{∾})+\frac{J_{x}-J_{y}}{2}sin(2α^{∾}) $ Откуда
$ J_{xy}cos(2α^{∾}) = J_{y}}{2}sin(2α^{∾}) $ Тогда
$ tg(2α^{∾}) = \frac{2J_{xy}}{J_{y}-J_{x}} $
$ α_{0} = α^{∾} $ Решения задачиИзменение осевых моментов инерции при повороте осей координат КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии