Изменение осевых моментов инерции при параллельном переносе осей координат Создано:
@nick
20 марта 2019
12:21
Создано:
@nick
20 марта 2019
12:21
Изменение осевых моментов инерции при параллельном переносе осей координат 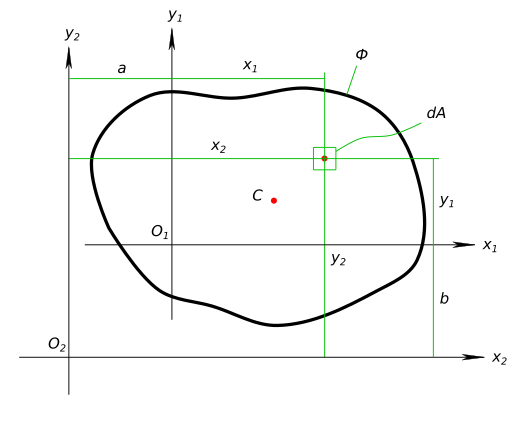
Изменение осевых моментов инерции при параллельном переносе осей координат Допустим в системе координат ...
$ x_{1}O_{1}y_{1} $ имеется плоская фигура ...
$ Ф $ Мы знаем площадь фигуры, ее осевые моменты инерции относительно осей x1 и y1 ...
$ A, J_{x_{1}}, J_{y_{1}} $ Необходимо вычислить осевые моменты инерции относительно осей новой системы координат ...
$ x_{2}O_{2}y_{2} $ если они параллельны осям первоначальной ...
$ x_{2}‖x_{1}, y_{2}‖y_{1} $ Расстояние между осями координат x1 и x2 равно ...
$ b $ между осями координат y1 и y2 равно ...
$ a $ Тогда осевые моменты инерции относительно осей x2 и y2 будут равны ...
$ J_{x_{2}}=\int\from{Ф}y_{2}^{2}dA=\int\from{Ф}(y_{1}+b)^{2}dA= $
$ = \int\from{Ф}(y_{1}^{2}+2by_{1}+b^{2})dA= $
$=\int\from{Ф}y_{1}^{2}dA+2b\int\from{Ф}y_{1}dA+b^{2}\int\from{Ф}dA=J_{x_{1}}+2bS_{x_{1}}+b^{2}A$ и
$ J_{y_{2}}=\int\from{Ф}x_{2}^{2}dA=\int\from{Ф}(x_{1}+a)^{2}dA= $
$ = \int\from{Ф}(x_{1}^{2}+2ax_{1}+a^{2})dA= $
$=\int\from{Ф}x_{1}^{2}dA+2a\int\from{Ф}x_{1}dA+a^{2}\int\from{Ф}dA=J_{y_{1}}+2aS_{y_{1}}+a^{2}A$ Теорема Штейнера Когда координатнатные оси x_{1}, y_{1} проходят через центр тяжести С:
$ S_{x_{1}}=0, S_{y_{1}}=0 $ тогда
$ J_{x_{2}}=J_{x_{1}}+b^{2}A $ и
$ J_{y_{2}}=J_{y_{1}}+a^{2}A $ Из множества параллельных осей та ближе к центру тяжести чей осевой момент инерции имеет наименьшее зачение. Решения задачиИзменение осевых моментов инерции при параллельном переносе осей координат КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии