Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольника АВС
Тема задачи: Точка, прямая линия и плоскость
Создано:
@yuliana2993
12 октября 2017
16:27
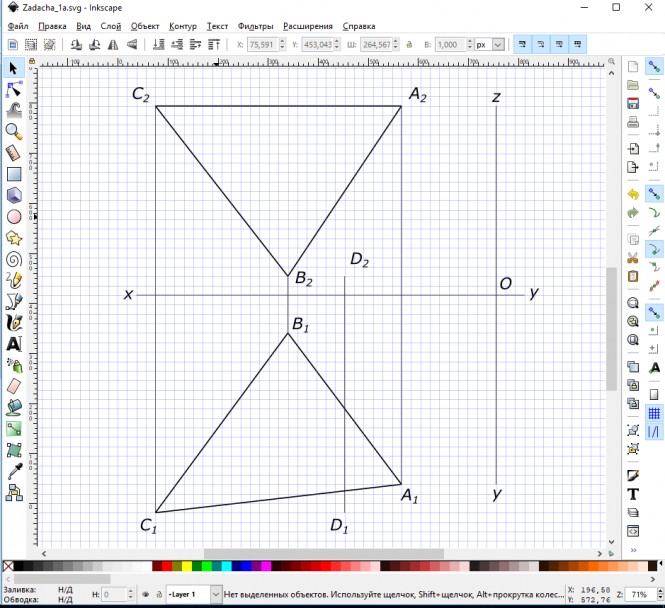
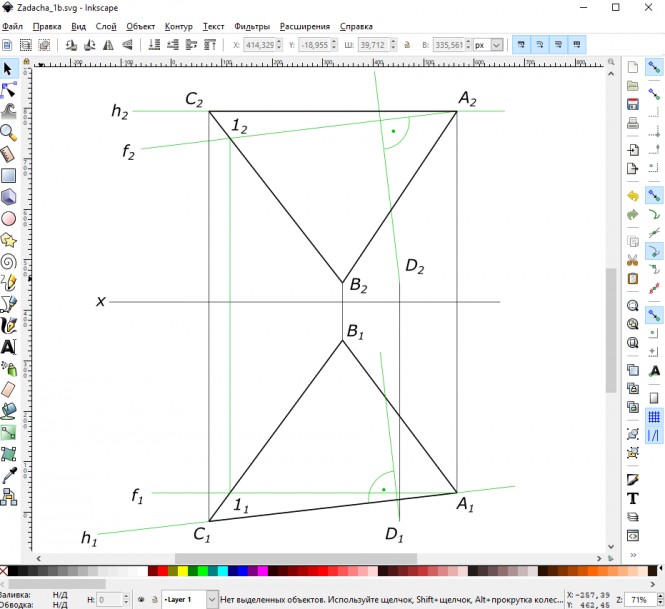
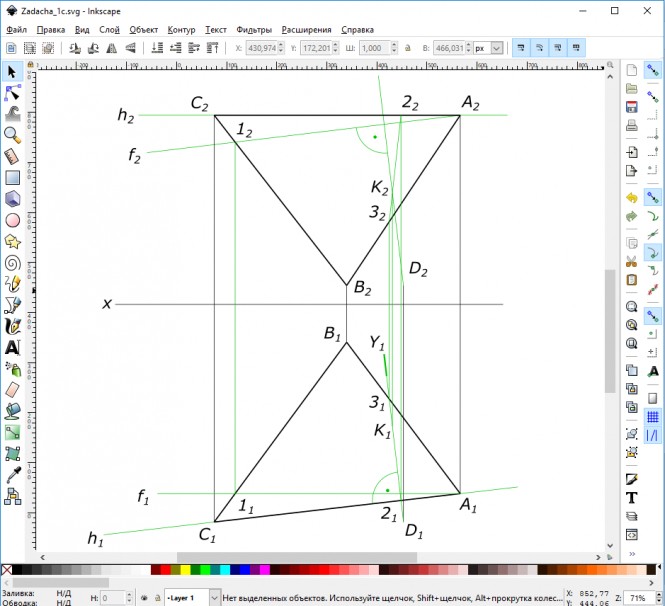
Дано: плоскость треугольника (А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной треугольником (А, В, С). Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольника(А, В, С). Данные для выполнения задачи взять из та6л. 3, в соответствии с вариантом. Указания к задаче 1. Задачу выполняют в такой последовательности: 1) из точки D опустить перпендикуляр, используя горизонталь h и фронталь f плоскости. При этом горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали f2; 2) определить точку пересечения перпендикуляра с плоскостью (А, В, С), для чего перпендикуляр (прямую) заключают во вспомогательную, обычно проецирующую, плоскость (γ), находят линию пересечения плоскости (А, В, С) и вспомогательной и отмечают точку К, в которой эта линия пересекается с перпендикуляром; 3) определяют натуральную величину (Н.В.) расстояния от точки D до плоскости (А, В, С), применяя способ прямоугольного треугольника; 4) видимость проекции перпендикуляра определяют методом конкурирующих точек. Номер варианта Значения координат, мм Ха=50, Уа=90, Za=100; Хв=110, Ув=20, Zв=10; Хс=180, Ус=115, Zc=100; Хd=80, Уd=115, Zd=10 Решения задачиПо заданным значениям координат, мм: Ха=50, Уа=90, Za=100; Хв=110, Ув=20, Zв=10; Хс=180, Ус=115, Zc=100; Хd=80, Уd=115, Zd=10 строим треугольник ABC и точку D 
Построение треугольника ABC и точки D КомментарииСледуя указаниям к задаче, выполняем ее в такой последовательности: 1) из точки D опустить перпендикуляр к плоскости ∆ ABC/ Строим горизонталь h(h1≡A1C1, h2≡A2C2) и фронталь f(f1//Ox, f2≡A2-12) плоскости. Строим перпендикуляр: его горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная перпендикулярна фронтальной проекции фронтали f2; 
Построение горизонтали и фронтали плоскости и перпендикуляра к ней Комментарии2) определить точку пересечения перпендикуляра с плоскостью ∆АВС: - перпендикуляр (прямую) заключаем во вспомогательную, проецирующую, плоскость Y; - находим линию пересечения плоскостей 2-3 и отмечаем точку К, в пересечении этой линии с перпендикуляром; 
Точка пересечения перпендикуляра с плоскостью Комментарии3) определяем натуральную величину (Н.В.) расстояния от точки D до плоскости ∆АВС, применяя способ прямоугольного треугольника; 4) видимость проекций перпендикуляра определяем методом конкурирующих точек.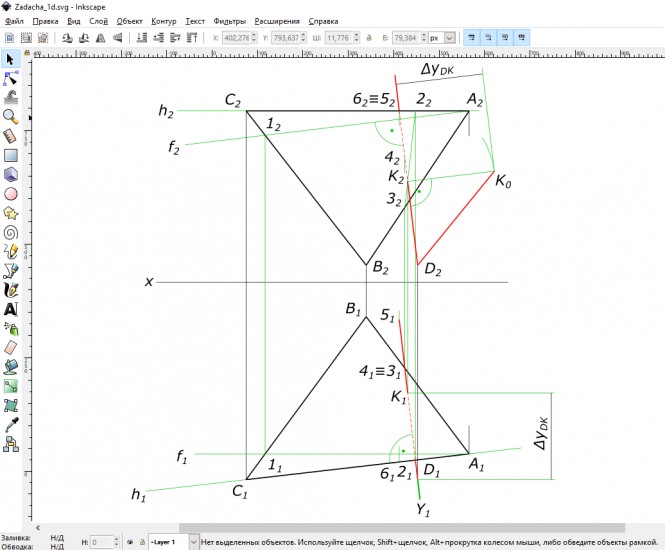 
Натуральная величина расстояния от точки D до плоскости ∆АВС, способ прямоугольного треугольника. Видимость проекций перпендикуляра методом конкурирующих точек КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Комментарии